FörberedandeFysik

Versionen från 22 januari 2010 kl. 12.21 (redigera) Lena Chytraeus (Diskussion | bidrag) ← Gå till föregående ändring		Nuvarande version (19 mars 2018 kl. 13.07) (redigera) (ogör) Louwah (Diskussion | bidrag)
(2 mellanliggande versioner visas inte.)
Rad 1:		Rad 1:
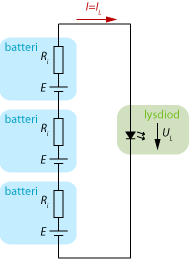
	Kirchhoffs spänningslag: <math>E-R_I\cdot I+E-R_I\cdot I+E-R_I\cdot I-U_L=0</math><br\>		Kirchhoffs spänningslag: <math>E-R_I\cdot I+E-R_I\cdot I+E-R_I\cdot I-U_L=0</math><br\>
	<math>3E-3R_I\cdot I-U_L=0</math><br\>		<math>3E-3R_I\cdot I-U_L=0</math><br\>
-	<math>3E=5,0 V</math><br\>	+	<math>3E=5,0 \,\mathrm{V}</math><br\>
-	<math>U_L=3,9V,I_L=1,0A \Rightarrow 5,0-3R_I-3,9=0 \Rightarrow 3R_I=1,1\Omega </math><br\>	+	<math>U_L=3,9\,\mathrm{V}, \,\, I_L=1,0 \,\mathrm{A} \Rightarrow 5,0-3R_I-3,9=0 \Rightarrow 3R_I=1,1\,\Omega </math><br\>
-	Effektutvecklingen i batteriet är <math>3R_I\cdot I^2=1,1W </math><br\>	+	Effektutvecklingen i batteriet är <math>3R_I\cdot I^2=1,1 \,\mathrm{W} </math><br\>
-	Effektutvecklingen i lysdioden är <math>U_L\cdot I_L=3,9W</math>	+	Effektutvecklingen i lysdioden är <math>U_L\cdot I_L=3,9 \,\mathrm{W}</math>
		+
		+
		+	[[Bild:losning_4_2_6.gif|center]]

---

Nuvarande version

Kirchhoffs spänningslag: \displaystyle E-R_I\cdot I+E-R_I\cdot I+E-R_I\cdot I-U_L=0
\displaystyle 3E-3R_I\cdot I-U_L=0
\displaystyle 3E=5,0 \,\mathrm{V}
\displaystyle U_L=3,9\,\mathrm{V}, \,\, I_L=1,0 \,\mathrm{A} \Rightarrow 5,0-3R_I-3,9=0 \Rightarrow 3R_I=1,1\,\Omega

Effektutvecklingen i batteriet är \displaystyle 3R_I\cdot I^2=1,1 \,\mathrm{W}
Effektutvecklingen i lysdioden är \displaystyle U_L\cdot I_L=3,9 \,\mathrm{W}