Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösning 4.5:7

FörberedandeFysik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
(Ny sida: Snells brytningformel: <math>n_1\cdot \sin\alpha _1 = n_2 \cdot \sin \alpha _2</math><br\> <math>n_1=1,0</math> och <math>n_2=1,33</math> <math>\alpha_1 = 30^\circ \Rightarrow</math>...)
Nuvarande version (23 mars 2018 kl. 14.58) (redigera) (ogör)
 
(En mellanliggande version visas inte.)
Rad 3: Rad 3:
<math>n_1\cdot \sin\alpha _1 = n_2 \cdot \sin \alpha _2</math><br\>
<math>n_1\cdot \sin\alpha _1 = n_2 \cdot \sin \alpha _2</math><br\>
-
<math>n_1=1,0</math> och <math>n_2=1,33</math> <math>\alpha_1 = 30^\circ
+
<math>n_1=1,0</math> och <math>n_2=1,33</math>, <math>\alpha_1 = 30^\circ
\Rightarrow</math><br\>
\Rightarrow</math><br\>
Rad 10: Rad 10:
Avståndet <math>b</math> fås ur sambandet <math>\tan \alpha _2 = b/d</math><br\>
Avståndet <math>b</math> fås ur sambandet <math>\tan \alpha _2 = b/d</math><br\>
-
<math>\tan 22^\circ = b/2,0 \Rightarrow b = 0,81 m</math><br\>
+
<math>\tan 22^\circ = b/2,0 \Rightarrow b = 0,81 \,\mathrm{m}</math><br\>
-
<math>\tan 30^\circ =(b+x)/2,0 \Rightarrow (b+x) = 1,15 m</math>
+
<math>\tan 30^\circ =(b+x)/2,0 \Rightarrow (b+x) = 1,15 \,\mathrm{m}</math>
-
<math>x = 1,15 - 0,81 = 0,34 m</math>
+
<math>x = 1,15 - 0,81 = 0,34 \,\mathrm{m}</math>
 +
 
 +
 
 +
[[Bild:losning_4_5_7.jpg]]

Nuvarande version

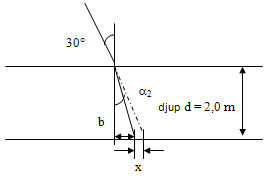
Snells brytningformel:

n1sin1=n2sin2

n1=10 och n2=133, 1=30

1005=133sin22=22

Avståndet b fås ur sambandet tan2=bd

tan22=b20b=081m

tan30=(b+x)20(b+x)=115m

x=115−081=034m


Bild:losning_4_5_7.jpg

Den här artikeln är hämtad från http://wiki.math.se/wikis/forberedandefysik/index.php/L%C3%B6sning_4.5:7