5.4 Övningar
FörberedandeFysik
| (En mellanliggande version visas inte.) | |||
| Rad 44: | Rad 44: | ||
<div class="ovning"> | <div class="ovning"> | ||
Väteatomens spektrum (Balmerserien) skall undersökas i det synliga området. Rydbergs formel för väteatomen kan skrivas: | Väteatomens spektrum (Balmerserien) skall undersökas i det synliga området. Rydbergs formel för väteatomen kan skrivas: | ||
| - | + | ||
| + | <math>\displaystyle \frac{1}{\lambda} = R\,\left( \displaystyle \frac{1}{n^2} - \displaystyle \frac{1}{k^2} \right)</math> | ||
a) Förklara ingående storheter. | a) Förklara ingående storheter. | ||
| Rad 60: | Rad 61: | ||
<div class="ovning"> | <div class="ovning"> | ||
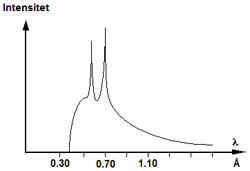
Ett röntgenrör har en anod bestående av Molybden. Vid en accelerationsspänning på <math>\mathrm{33\, kV}</math> över röntgenröret uppmäts nedanstående spektrum. | Ett röntgenrör har en anod bestående av Molybden. Vid en accelerationsspänning på <math>\mathrm{33\, kV}</math> över röntgenröret uppmäts nedanstående spektrum. | ||
| + | |||
| + | [[Bild:ovn546.jpg]] | ||
Rita en skiss av ett röntgenrör och beräkna med hjälp av diagrammet | Rita en skiss av ett röntgenrör och beräkna med hjälp av diagrammet | ||
Nuvarande version
| Teori | Övningar |
Övning 5.4:1
Beräkna med hjälp av Bohrs postulat elektronens hastighet i väte i de energinivåer som ges av huvudkvanttalet \displaystyle n. Antag att elektronen befinner sig i en exiterad nivån med \displaystyle n=2 under \displaystyle 10^{-8}\mbox{ s}.
Hur många varv hinner elektronen göra i detta tillstånd, innan den faller ned till grundtillståndet? Banan kan anses vara cirkulär.
Övning 5.4:2
För att åstadkomma en \displaystyle H\alpha-övergång i Lymanserien (övergång från \displaystyle n=2 till \displaystyle n=1) beskjuts väteatomer i grundtillståndet med elektroner.
a) Vilken energi och deBroglievåglängd måste dessa bombarderande elektroner åtminstone ha?
b) Vilken hastighet får den rekylerande väteatomen vid den åtföljande foton emissionen.
Övning 5.4:3
Vilka av linjerna i vätets spektrum faller inom den synliga delen av våglängdsspektrum \displaystyle \mathrm{(400\, –\, 700\, nm)}? Vilka linjer hos \displaystyle \mathrm{He^+} faller inom samma del ? Utförlig motivering med ekvationer skall göras.
Övning 5.4:4
I en vakuumspektrograf tar man upp absorptionsspektrum från dubbeljoniserat litium \displaystyle \mathrm{(Li)}, så att den endast har en elektron kvar i höljet.
a) Vilket är den längsta våglängd som man observerar?
b) Hur stor energi i elektronvolt åtgår för att ta bort den sista elektronen?
Övning 5.4:5
Väteatomens spektrum (Balmerserien) skall undersökas i det synliga området. Rydbergs formel för väteatomen kan skrivas:
\displaystyle \displaystyle \frac{1}{\lambda} = R\,\left( \displaystyle \frac{1}{n^2} - \displaystyle \frac{1}{k^2} \right)
a) Förklara ingående storheter.
b) Använd formeln för att bestämma den kortaste våglängden i Balmerserien.
c) Beräkna den längsta våglängden som kan ses i Balmerserien.
d) Vilka våglängder kan observeras om man exciterat atomen så att nivå \displaystyle k=4 är populerad?
Övning 5.4:6
Ett röntgenrör har en anod bestående av Molybden. Vid en accelerationsspänning på \displaystyle \mathrm{33\, kV} över röntgenröret uppmäts nedanstående spektrum.
Rita en skiss av ett röntgenrör och beräkna med hjälp av diagrammet
a) Plancks konstant, \displaystyle h.
b) energiskillnaden mellan \displaystyle \mathrm{L}-och \displaystyle \mathrm{K}-skalet
c) våglängden för \displaystyle \mathrm{L_\alpha} - strålningen.
Övning 5.4:7
Visa att våglängden för \displaystyle \mathrm{K_\alpha} linjen hos ett tungt grundämne med atomnumret Z kan skrivas som \displaystyle \mathrm{\lambda \approx \displaystyle \frac{1220}{Z^2},Å}
 Hämtar...
Hämtar...