3.6 Cirkulär och harmonisk rörelse
FörberedandeFysik
| Rad 130: | Rad 130: | ||
[[Bild:fjader.jpg|center]] | [[Bild:fjader.jpg|center]] | ||
| - | En liten kropp ligger på ett horisontellt glatt bord. Den är kopplad med en fjäder till en | + | En liten kropp ligger på ett horisontellt glatt bord. Den är kopplad med en fjäder till en fast punkt. Vi låter <math>y</math> vara fjäderns förlängning. Det betyder att om <math>y=0</math>, är fjädern |
| - | fast punkt. Vi låter y | + | ospänd och om <math>y < 0</math> är fjädern ihoptryckt. |
| - | ospänd och om y<0 är fjädern ihoptryckt. | + | |
| + | En experimentell lag säger att fjäderns kraft på partikeln är <math>F=ky</math>, där <math>k</math> kallas fjäderkonstanten och förstås är positiv och beroende av fjädern. <math>F</math> verkar i den negativa <math>y</math>-riktningen. Vi får <math>-ky=ma=>a=-\frac{k}{m}y</math> som är en harmonisk svängningsekvation med <math>\omega ^2=\frac{k}{m}</math> | ||
| - | En experimentell lag säger att fjäderns kraft på partikeln är F=ky , där k kallas | ||
| - | fjäderkonstanten och förstås är positiv och beroende av fjädern. F verkar i den negativa | ||
| - | y -riktningen. Vi får Àky=ma=>a=Àkmy som är en harmonisk svängningsekvation med | ||
| - | !2=km | ||
<div class="inforuta" style="width: 580px"> | <div class="inforuta" style="width: 580px"> | ||
===Råd för inläsning=== | ===Råd för inläsning=== | ||
Versionen från 22 december 2009 kl. 14.44
| Teori | Övningar |
Mål och innehåll
Innehåll
- Mekanikens lagar i vektorform
- Cirkulär rörelse med konstant hastighet
- Den allmänna gravitationen
- Harmonisk svängningsrörelse
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Definiera rörelsemänd i vektorform.
- Definiera fjäderkonstanten.
- Redogöra för gravitationslagen.
- Redogöra för fjäderlagen.
- Redogöra för harmonisk svängningsrörelse.
- Förkara vad som menas med centripetalacceleration.
- Förkara varför en fjäder kan åstadkomma en harmonisk svängningsrörelse.
- Ställa upp och räkna ut vilka krafter som verkar vid en cirulärrörelse.
- Ställa upp och räkna ut vilka krafter som verkar vid en harmonisk svängningsrörelse.
Mekanikens lagar i vektorform
Tidigare i kinematikdelen av denna kurs har vi definierat hastighet och acceleration i x- och y-riktningar. Eftersom riktningar ingår i specificeringen av hastighet och acceleration, är dessa storheter vektorer på samma sätt som en kraft är en vektorstorhet. De kan representeras som vektorer
Hastighet representeras som \displaystyle v och acceleration som \displaystyle a.
En kraft representeras som \displaystyle F.
Rörelsemängd, som också den är en vektorstorhet, representeras som \displaystyle p.
Newtons kraftekvation kan skrivas i vektorform som \displaystyle F=ma och rörelsemängd definieras som \displaystyle p=mv.
Kom ihåg att energi och arbete inte är vektorer på samma sätt som massa inte är en vektor.
Vad är fördelen med att skriva ekvationer som vektorer?
Då kan vi tillämpa hela den matematiska teorin som kallas vektorlära för att utveckla mekaniken.
Till exempel \displaystyle F=ma kan tolkas som att kraftsumman i en viss riktning är lika med massa gånger acceleration i samma riktning. Om man observerar att en partikel har en acceleration \displaystyle a, kan man dra slutsatsen att en kraft \displaystyle ma verkar på partikeln.
Likaså kan \displaystyle P=mv tolkas som att rörelsemängd i en viss riktning är lika med massa gånger hastighet i samma riktning.
Cirkulär rörelse med konstant hastighet
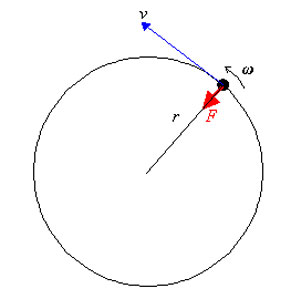
Vi har i kinematikdelen behandlat en partikel som rör sig med konstant fart i en cirkelbana.
Trots att partikeln har konstant fart har den en centripetalacceleration \displaystyle \frac{v^2}{r} som är riktad inåt mot cirkelcentrum, d v s att centripetalacceleration har konstant storlek med riktning som ändras hela tiden. Enligt kraftekvationen \displaystyle F=ma måste det finnas en kraft \displaystyle F=m\frac{v^2}{r} som är riktad inåt mot cirkelcentrum.
Ett exempel på hur man kan demonstrera denna teori är följande:
Vi har ett glatt(friktionsfritt) horisontellt bord. Vi fäster ett snöre med längd \displaystyle r vid en punkt på bordet och i andra ändan fäster vi en liten boll med massan \displaystyle m. Sedan sätter vi igång bollen i en cirkulär rörelse.
Om vi mäter spännkraften i snöret, ser vi att den har ett värde \displaystyle ma där \displaystyle a är centripetalaccelerationen
\displaystyle \omega ^2r och \displaystyle \omega =\frac{2\pi}{T}.
\displaystyle T är perioden d v s tiden för ett varv.
Den allmänna gravitationen
Planeterna och kometerna kretsar kring solen i sina elliptiska banor. Gravitationskraften från solen på planeterna och kometerna håller dem i banorna. Här skall vi dock endast diskutera cirkulära banor varför vi endast behandlar människotillverkade satelliter som kretsar kring jorden i en cirkelbana.
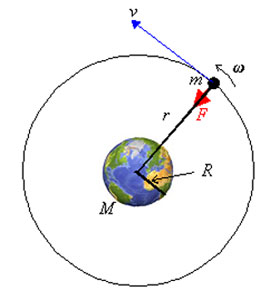
Figuren visar en satellit som kretsar kring jorden i en cirkulär bana med radien \displaystyle r.
Enligt Newtons gravitationsteori utsätts satelliten för en gravitationskraft \displaystyle F som beror på satellitens avstånd till jordens centrum, i detta fall \displaystyle r.
\displaystyle F=G\frac{Mm}{r^2} där \displaystyle M är jordens massa och \displaystyle m är satellitens massa. Konstanten \displaystyle G kallas för gravitationskonstanten. Gravitationskonstanten \displaystyle G har ett extremt litet värde. Det är endast på grund av att astronomiska kroppar är så massiva som gravitationskraften har icke-försumbara värden inom astronomi och kosmologi.
Om man känner till jordens radie \displaystyle R (närmare 640 mil) kan man undvika \displaystyle G och \displaystyle M.
En partikel med massan \displaystyle m på jordytan har en gravitationskraft på den lika med
\displaystyle G=\frac{Mm}{r^2}. Detta är förstås samma sak som partikelns tyngd \displaystyle mg.
Vi får \displaystyle G\frac{Mm}{r^2}=mg eller \displaystyle GMm=mgR^2 så att \displaystyle F=\frac{mgR^2}{r^2}.
Slutligen kan vi tillämpa kraftekvationen.
Gravitationskraften på satelliten är lika med satellitens massa gånger dess centripetalacceleration.
\displaystyle F=G\frac{Mm}{r^2}=m\frac{v^2}{r}
Eller
\displaystyle \frac{mgR^2}{r^2}=m\frac{v^2}{r}=m\omega ^2r
Harmonisk svängningsrörelse
Enligt teorin för harmonisk svängningsrörelse gäller att \displaystyle a=-\omega ^2y.
Enligt kraftekvationen \displaystyle F=ma, där \displaystyle F är kraften på en liten kropp (partikel) med massan \displaystyle m.
\displaystyle \Rightarrow En kraft \displaystyle F=-m\omega ^2y ger upphov till harmonisk svängningsrörelse.
Obs. Kraften är inte konstant. Den är maximal vid rörelsens utkant \displaystyle (y=±amplituden) och är noll vid rörelsens mittpunkt.
Man kan åstadkomma harmonisk svängningsrörelse med en fjäder.
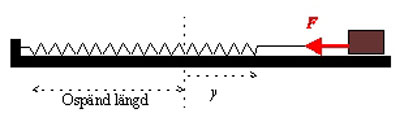
En liten kropp ligger på ett horisontellt glatt bord. Den är kopplad med en fjäder till en fast punkt. Vi låter \displaystyle y vara fjäderns förlängning. Det betyder att om \displaystyle y=0, är fjädern ospänd och om \displaystyle y < 0 är fjädern ihoptryckt.
En experimentell lag säger att fjäderns kraft på partikeln är \displaystyle F=ky, där \displaystyle k kallas fjäderkonstanten och förstås är positiv och beroende av fjädern. \displaystyle F verkar i den negativa \displaystyle y-riktningen. Vi får \displaystyle -ky=ma=>a=-\frac{k}{m}y som är en harmonisk svängningsekvation med \displaystyle \omega ^2=\frac{k}{m}
Råd för inläsning
Lästips
- För dig som behöver en längre förklaring eller vill fördjupa sig ytterligare vill vi tipsa om:
- HEUREKA! Fysik kurs B, kapitel 6: avsnitt 1-4.
Länktips
- Klicka på länken ovan och sedan på 7.1.2 i mitten högst upp. Försök att resonera fram svaret själv utan att titta på lösningen. Experimentet illustrerar att när en partikel rör sig i en cirkel, måste en kraft verka på partikeln som är riktad mot cirkelns centrum.
- Nedan finns en länk till en applet om svängningsrörelse för en fjäder,men tyvärr har de vänt på fjädern, så att det finns risk att du kan blanda ihop förlängning och förkortning, om du inte ser detta. Annars är övningen bra.
- Experimentera och lär dig mera om hur krafterna i en fjäderpendel fungerar=====länk fungerar inte=====
- Experimentera och lär dig mer om hur elongation, hastighet, tangentiell acceleration, kraft och energi varierar när en plan pendel rör sig =====länk fungerar inte=====