Lösning 3.3:3
FörberedandeFysik
(Skillnad mellan versioner)
| Rad 6: | Rad 6: | ||
[[Bild:losning_3_3_3.2.jpg]] | [[Bild:losning_3_3_3.2.jpg]] | ||
| + | |||
| + | Kraftsumman på lådan nedför planet är <math>Mg\cos60^\circ</math> | ||
| + | |||
| + | Om <math>a</math> är lådans acceleration, får vi enligt kraftekvationen | ||
| + | |||
| + | <math>Mg\cos60^\circ=Ma \Rightarrow g\cos60^\circ =a \Rightarrow a=5m/s^2</math><br\> | ||
| + | |||
| + | <math>s=v_0t+\frac{1}{2}at^2 \Rightarrow s=(4m/s)(3s)+ \frac{1}{2}(5m/s^2)(3s)^2=34,5s</math> | ||
Versionen från 11 januari 2010 kl. 10.43
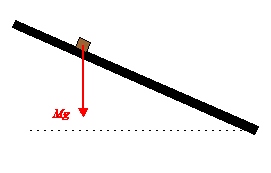
Låt massan vara M. Det betyder att tyngdkraften är \displaystyle Mg.
Vi är endast intresserade av tyngdkraftens påverkan längs planet.
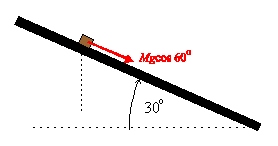
Kraftsumman på lådan nedför planet är \displaystyle Mg\cos60^\circ
Om \displaystyle a är lådans acceleration, får vi enligt kraftekvationen
\displaystyle Mg\cos60^\circ=Ma \Rightarrow g\cos60^\circ =a \Rightarrow a=5m/s^2
\displaystyle s=v_0t+\frac{1}{2}at^2 \Rightarrow s=(4m/s)(3s)+ \frac{1}{2}(5m/s^2)(3s)^2=34,5s