Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösning 3.6:2

FörberedandeFysik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
(Ny sida: a) Om nollnivån sätts vid utgångsläget eftersom utgångshastigheten då är noll, är den totala energin noll. Vid lägsta läget har kulan den totala energin 21mv2Àmg(40cm) där m ...)
Rad 1: Rad 1:
a) Om nollnivån sätts vid utgångsläget eftersom utgångshastigheten då är noll, är den totala energin noll.
a) Om nollnivån sätts vid utgångsläget eftersom utgångshastigheten då är noll, är den totala energin noll.
-
Vid lägsta läget har kulan den totala energin 21mv2Àmg(40cm) där m är kulans massa.
+
Vid lägsta läget har kulan den totala energin <math>\frac{1}{2}mv^2 - mg(40 cm)</math> där <math>m</math> är kulans massa.
-
)21mv2Àmg(40cm=0)v2=2g(40cm)=8(m/s)2)v=2p2m/s=2;83m/s
+
<math>\Rightarrow \frac{1}{2}mv^2 - mg(40cm) = 0 \Rightarrow v^2 = 2g(40cm)=8(m/s)^2 \Rightarrow v=2\sqrt{2}m/s = 2,83 m/s</math>
-
b) Centripetalaccelerationen är v2radie=40cm8(m/s)2=20m=s2
+
b) Centripetalaccelerationen är <math>\frac{v^2}{radie} = \frac{8(m/s)^2}{40cm} = 20 m/s^2</math>
-
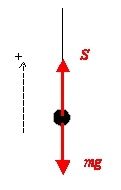
c) Kraftsumman med positiv uppåt är SÀmg .
+
c) Kraftsumman med positiv uppåt är <math>S - mg</math>.
-
Kraftekvationen med positiv uppåt ger SÀmg=m(20m=s2))S=150N
+
Kraftekvationen med positiv uppåt ger <math>S - mg = m(20m/s^2) \Rightarrow S = 150N</math>
[[Bild:losning_3_6_2.jpg]]
[[Bild:losning_3_6_2.jpg]]

Versionen från 15 januari 2010 kl. 11.52

a) Om nollnivån sätts vid utgångsläget eftersom utgångshastigheten då är noll, är den totala energin noll.

Vid lägsta läget har kulan den totala energin 21mv2−mg(40cm) där m är kulans massa.

21mv2−mg(40cm)=0v2=2g(40cm)=8(ms)2v=22ms=283ms 


b) Centripetalaccelerationen är v2radie=40cm8(ms)2=20ms2


c) Kraftsumman med positiv uppåt är S−mg.

Kraftekvationen med positiv uppåt ger S−mg=m(20ms2)S=150N

Bild:losning_3_6_2.jpg

Den här artikeln är hämtad från http://wiki.math.se/wikis/forberedandefysik/index.php/L%C3%B6sning_3.6:2