5.4 Atomen
FörberedandeFysik
| Rad 60: | Rad 60: | ||
# Integralen av elektronens rörelsemängd <math>p</math> runt elektronbanan är en heltalsmultipel av <math> h</math>. <math>\oint p\, ds = n\, h</math> | # Integralen av elektronens rörelsemängd <math>p</math> runt elektronbanan är en heltalsmultipel av <math> h</math>. <math>\oint p\, ds = n\, h</math> | ||
| - | Eftersom elektronerna rör sig med konstant hastighet i en cirkulär bana < | + | Eftersom elektronerna rör sig med konstant hastighet i en cirkulär bana <math>s</math> |
| - | med konstant avstånd < | + | med konstant avstånd <math>r</math> till kärnan kommer rörelsemomentet <math>p</math> i postulat 3 ovan att vara oberoende av banan. Vi får för VL |
| - | < | + | <math>\oint p ds = p \oint ds = pr \int\limits_0^{2\pi}d\theta = pr\cdot 2\pi</math> |
| - | Då < | + | Då <math>p = mv</math> kan vi nu skriva postulat 3 som |
| - | < | + | <math>mv \cdot 2\pi = nh \iff v =\displaystyle \frac{n h}{2\pi m r}</math> |
| - | där < | + | där <math>n</math> är ett positivt heltal, <math>h</math> Plancks konstant, <math>r</math> avståndet mellan |
| - | elektronen och kärnan, < | + | elektronen och kärnan, <math>v</math> elektronens hastighet och <math>m</math> elektronens massa. |
| Rad 77: | Rad 77: | ||
En elektron i en omloppsbana kring en atomkärna påverkas av två krafter, | En elektron i en omloppsbana kring en atomkärna påverkas av två krafter, | ||
| - | coulombkraften och centipetalkraften. Dessa är lika stora. I < | + | coulombkraften och centipetalkraften. Dessa är lika stora. I <math>r</math>-led har vi alltså |
| - | med laddningen < | + | med laddningen <math>q = e</math> följande |
| - | < | + | <math>\displaystyle\frac{e^2}{4\pi \epsilon_0 r^2} = \displaystyle\frac{m v^2}{r}</math> |
| - | där < | + | där <math>\epsilon_0</math> är kapacitiviteten i rymden, |
| - | < | + | <math>\epsilon_0 \approx 8,854 \cdot 10^{-12} \,\mbox{F/m}</math> |
| - | Om vi kombinerar de båda senaste sambanden får vi < | + | Om vi kombinerar de båda senaste sambanden får vi <math>r</math> som en funktion av <math>n</math> |
enligt | enligt | ||
| - | < | + | <math> |
\displaystyle\frac{e^2}{4 \pi\epsilon_0 r^2} | \displaystyle\frac{e^2}{4 \pi\epsilon_0 r^2} | ||
= \displaystyle\frac{m}{r} \cdot \bigg(\displaystyle\frac{nh}{2 \pi m r}\bigg)^2 | = \displaystyle\frac{m}{r} \cdot \bigg(\displaystyle\frac{nh}{2 \pi m r}\bigg)^2 | ||
\Rightarrow r_n = \displaystyle\frac{ \epsilon_0 h^2}{m e^2 \pi}\cdot n^2 | \Rightarrow r_n = \displaystyle\frac{ \epsilon_0 h^2}{m e^2 \pi}\cdot n^2 | ||
| - | = a_0\cdot n^2</ | + | = a_0\cdot n^2</math> |
| - | där < | + | där <math>a_0</math> är Bohrradien, <math>a_0= 0{,}0529 \,\mbox{nm}</math> |
| - | Elektronens energi, < | + | Elektronens energi, <math>E</math>, utan hänsyn tagen till viloenergin, är summan av |
den kinetiska och den potentiella energin. | den kinetiska och den potentiella energin. | ||
| - | < | + | <math>E = \displaystyle\frac{1}{2} m v^2 - \displaystyle\frac{e^2}{4 \pi \epsilon_0 r} |
= \displaystyle\frac{1}{2}m \,v^2 - m \,v^2 = - \frac{1}{2} m\,v^2 | = \displaystyle\frac{1}{2}m \,v^2 - m \,v^2 = - \frac{1}{2} m\,v^2 | ||
| - | = - \displaystyle\frac{e^2}{8 \pi \epsilon_0 r}</ | + | = - \displaystyle\frac{e^2}{8 \pi \epsilon_0 r}</math> |
Energin är negativ eftersom elektronen är bunden till kärnan. | Energin är negativ eftersom elektronen är bunden till kärnan. | ||
| Rad 112: | Rad 112: | ||
| - | Om vi sätter in vårt uttryck för < | + | Om vi sätter in vårt uttryck för <math>r</math> i detta får vi <math>E</math> som en funktion |
| - | av < | + | av <math>n</math> |
| - | < | + | <math>E_n = - \displaystyle\frac{e^2}{8 \pi \epsilon_0} \cdot \frac{m e^2 \pi}{n^2 \epsilon_0 |
h^2} | h^2} | ||
= - \displaystyle\frac{m e^4}{8 h^2 \epsilon_0^2} \cdot \displaystyle\frac{1}{n^2} | = - \displaystyle\frac{m e^4}{8 h^2 \epsilon_0^2} \cdot \displaystyle\frac{1}{n^2} | ||
| - | = E_0 \cdot \frac{1}{n^2}</ | + | = E_0 \cdot \frac{1}{n^2}</math> |
| - | där < | + | där <math>E_0</math> är vätets joniseringsenergi, den energi som måste tillföras för att en atom i viloläge ska frigöra en elektron helt. Med numeriska värden för <math>m</math>, <math>e</math>, <math>h</math> och <math>\epsilon_0</math> får vi <math>E_0 = -13{,}61 \,\mbox{eV}</math>. |
Vi har alltså för en elektron i omloppsbana energisambandet | Vi har alltså för en elektron i omloppsbana energisambandet | ||
| - | < | + | <math>E_n = E_0\cdot \displaystyle \frac{1}{n^2} = -13{,}61\cdot \displaystyle\frac{1}{n^2} \,\mbox{eV}</math> |
| - | där < | + | där <math>n</math> är huvudkvanttalet och kan anta värdena <math>1,2,3,\dots</math> |
''Mer material kommer'' | ''Mer material kommer'' | ||
Versionen från 5 december 2017 kl. 15.06
| Teori | Övningar |
Mål och innehåll
Innehåll:
- Atomen
- Bohrs tre postulat
- Energinivåer
- Laser
- Stimulerad emission
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Definiera Balmervåglängderna (Rydbergs formel för väte).
- Redogöra för Bohrs tre postulat energinivåernas kvantisering.
- Förklara hur en laser fungerar.
- Ställa upp och beräkna våglängden vid atomövergångar.
FÖRFATTARE: Göran Tranströmer & Lars-Erik Berg, KTH Fysik
Atomen
Spektroskopin gav att varje grundämne har ett karakteristiskt spektrum. För vissa ämnen (väte, vissa alkalimetaller) var spektrallinjerna regelbundna, lätt igenkännliga serier. Balmer fann för de synliga våglängderna i vätets spektrum att
\displaystyle \lambda_n = konst \cdot \displaystyle \frac{n^2}{n^2 - 2^2}
där \displaystyle n är det skal som elektronen exciteras till, \displaystyle n = 3,4,5... Längre fram i teorin visar vi hur vi kommer fram till detta samband.
- Balmerserien hos atomärt väte.
Bohrs teori för väteatomen
Uppmuntrad av Plancks framgång med kvantisering kom Bohrs teori för väteatomen (1913). Den innebar att i ett bundet (atomärt) system är energin kvantiserad. Systemets möjliga energitillstånd kan åskådliggöras med ett energinivådiagram, där (i den enklaste modellen) varje nivå tilldelas ett kvanttal \displaystyle n. Genom absorption av elektromagnetisk strålning eller genom kollisioner med omgivande atomer överförs kinetisk energi till elektronen, som exciteras; den motsatta deexcitationsprocessen sker under fotonemission.
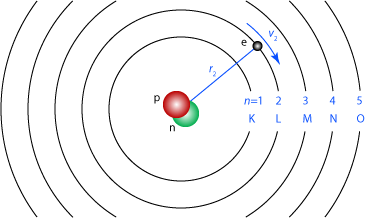
Runt en proton med laddningen \displaystyle \mathrm{e^+} kretsar en elektron med motsatt laddning. Protonens massa är 1836 gånger tyngre än elektronens, så i den enklaste beskrivningen rör sig elektronen i en cirkulär bana runt den stillaliggande (oändligt tunga) protonen.
Banorna kallas skal, och betecknas med bokstäver i alfabetisk ordning inifrån och ut, där det innerska skalet betecknas K. Ett sätt att beteckna hopp mellan skal är att använda det grekiska alfabetet. K\displaystyle _\alpha betecknar ett hopp som hoppar över noll andra skal, så det är detsamma som ett hopp från L-skalet till K-skalet. \displaystyle \beta betecknar hopp som hoppar över ett skal, så K\displaystyle _\beta betecknar ett hopp från M-skalet till K-skalet. L\displaystyle _\beta betecknar ett hopp från N-skalet till L-skalet.
På samma sätt betecknar \displaystyle \gamma ett hopp som hoppar över två skal, och så vidare.
Bohrs tre postulat
- Elektronen kretsar i stabila banor utan att stråla ut energi.
- Då elektronen övergår från en stabil bana till en annan stabil bana absorberar eller emitterar den energin \displaystyle E_i - \,E_f = hf_{if}
- Integralen av elektronens rörelsemängd \displaystyle p runt elektronbanan är en heltalsmultipel av \displaystyle h. \displaystyle \oint p\, ds = n\, h
Eftersom elektronerna rör sig med konstant hastighet i en cirkulär bana \displaystyle s med konstant avstånd \displaystyle r till kärnan kommer rörelsemomentet \displaystyle p i postulat 3 ovan att vara oberoende av banan. Vi får för VL
\displaystyle \oint p ds = p \oint ds = pr \int\limits_0^{2\pi}d\theta = pr\cdot 2\pi
Då \displaystyle p = mv kan vi nu skriva postulat 3 som
\displaystyle mv \cdot 2\pi = nh \iff v =\displaystyle \frac{n h}{2\pi m r}
där \displaystyle n är ett positivt heltal, \displaystyle h Plancks konstant, \displaystyle r avståndet mellan elektronen och kärnan, \displaystyle v elektronens hastighet och \displaystyle m elektronens massa.
En elektron i en omloppsbana kring en atomkärna påverkas av två krafter,
coulombkraften och centipetalkraften. Dessa är lika stora. I \displaystyle r-led har vi alltså
med laddningen \displaystyle q = e följande
\displaystyle \displaystyle\frac{e^2}{4\pi \epsilon_0 r^2} = \displaystyle\frac{m v^2}{r}
där \displaystyle \epsilon_0 är kapacitiviteten i rymden,
\displaystyle \epsilon_0 \approx 8,854 \cdot 10^{-12} \,\mbox{F/m}
Om vi kombinerar de båda senaste sambanden får vi \displaystyle r som en funktion av \displaystyle n enligt
\displaystyle \displaystyle\frac{e^2}{4 \pi\epsilon_0 r^2} = \displaystyle\frac{m}{r} \cdot \bigg(\displaystyle\frac{nh}{2 \pi m r}\bigg)^2 \Rightarrow r_n = \displaystyle\frac{ \epsilon_0 h^2}{m e^2 \pi}\cdot n^2 = a_0\cdot n^2
där \displaystyle a_0 är Bohrradien, \displaystyle a_0= 0{,}0529 \,\mbox{nm}
Elektronens energi, \displaystyle E, utan hänsyn tagen till viloenergin, är summan av
den kinetiska och den potentiella energin.
\displaystyle E = \displaystyle\frac{1}{2} m v^2 - \displaystyle\frac{e^2}{4 \pi \epsilon_0 r}
= \displaystyle\frac{1}{2}m \,v^2 - m \,v^2 = - \frac{1}{2} m\,v^2
= - \displaystyle\frac{e^2}{8 \pi \epsilon_0 r}
Energin är negativ eftersom elektronen är bunden till kärnan.
Om vi sätter in vårt uttryck för \displaystyle r i detta får vi \displaystyle E som en funktion
av \displaystyle n
\displaystyle E_n = - \displaystyle\frac{e^2}{8 \pi \epsilon_0} \cdot \frac{m e^2 \pi}{n^2 \epsilon_0 h^2}
= - \displaystyle\frac{m e^4}{8 h^2 \epsilon_0^2} \cdot \displaystyle\frac{1}{n^2}
= E_0 \cdot \frac{1}{n^2}
där \displaystyle E_0 är vätets joniseringsenergi, den energi som måste tillföras för att en atom i viloläge ska frigöra en elektron helt. Med numeriska värden för \displaystyle m, \displaystyle e, \displaystyle h och \displaystyle \epsilon_0 får vi \displaystyle E_0 = -13{,}61 \,\mbox{eV}.
Vi har alltså för en elektron i omloppsbana energisambandet
\displaystyle E_n = E_0\cdot \displaystyle \frac{1}{n^2} = -13{,}61\cdot \displaystyle\frac{1}{n^2} \,\mbox{eV}
där \displaystyle n är huvudkvanttalet och kan anta värdena \displaystyle 1,2,3,\dots
Mer material kommer