5.5 Kärnan
FörberedandeFysik
| Rad 226: | Rad 226: | ||
Det radioaktiva strålningen som upptäcktes av Becquerel (1896) kan innehålla tre olika komponenter | Det radioaktiva strålningen som upptäcktes av Becquerel (1896) kan innehålla tre olika komponenter | ||
| - | * < | + | * <math>\alpha</math>-partiklar (som är heliumkärnor) |
| - | * < | + | * <math>\beta</math>-partiklar (som är elektroner eller positroner) |
| - | * < | + | * <math>\gamma</math>-partiklar (som är fotoner) |
I sällsynta fall kan också neutroner och stora kärnfragment förekomma. | I sällsynta fall kan också neutroner och stora kärnfragment förekomma. | ||
| - | Antalet sönderfall från ett radioaktivt ämne avtar exponentiellt. Sannolikheten att en kärna skall sönderfalla på tiden < | + | Antalet sönderfall från ett radioaktivt ämne avtar exponentiellt. Sannolikheten att en kärna skall sönderfalla på tiden <math>dt</math> (<math>dt</math> är så liten att <math>dt \ll 1</math>) är <math>dt</math>. Om det finns <math>N</math> radioaktiva kärnor vid tiden <math>t</math>, så sönderfaller antalet kärnor (därav minustecknet) |
| - | < | + | <math> -\,\displaystyle\frac{dN}{dt} = N</math> |
med lösningen | med lösningen | ||
| - | < | + | <math>N = N_0 e^{-\lambda t}</math> |
| - | < | + | <math>N_0</math> är antalet kärnor vid tiden <math>t=0</math> och <math>\lambda</math> är sönderfallskonstanten som är olika för olika nuklider, Den beror av växelverkan mellan kärnan och de innersta elektronerna i atomen och är därför oberoende av om atomerna bildar en gas, vätska eller en fast kropp. |
| - | Om man känner halveringstiden, den tid det tar för < | + | Om man känner halveringstiden, den tid det tar för <math>N</math> att halveras, kan man enkelt plocka fram konstanten <math>\lambda</math>. |
| - | < | + | <math>N_{T/2} = \displaystyle\frac{N_0}{2}</math> |
| - | < | + | <math>N_{T/2} = N_0e^{-\lambda T_{1/2}} </math> |
Sätts dessa lika finner man | Sätts dessa lika finner man | ||
| - | < | + | <math>T_{1/2}=\displaystyle\frac{\ln 2}{\lambda}</math> |
| - | Aktiviteten (decay rate) < | + | Aktiviteten (decay rate) <math>R</math>, definieras som antalet sönderfall/tidsenhet och kan skrivas |
| - | < | + | <math> R = -\,\displaystyle\frac{dN}{dt} = -\,\displaystyle\frac{d}{dt} N_0 e^{-\lambda t} = +\lambda N_0 e^{-\lambda t} = R_0 e^{-\lambda t} </math> |
vilket också kan skrivas | vilket också kan skrivas | ||
| - | < | + | <math> R = \lambda N </math> |
| - | Aktiviteten mäts i enheten < | + | Aktiviteten mäts i enheten <math>1 \mbox{ Bq}</math> (Becquerel) = 1 sönderfall/s. |
| - | Tidigare användes enheten < | + | Tidigare användes enheten <math>1 \mbox{ Cu}</math> (Curie) <math> = 3,7\cdot10^7\:\mbox{Bq}</math>. |
==Hur tar man reda på antalet kärnor i ett prov?== | ==Hur tar man reda på antalet kärnor i ett prov?== | ||
Avogadros tal <math>N_A = 6,022 \cdot 10^{23}</math> talar om hur många kärnor vi har per mol, där en mol är så många gram som formelvikten anger. Antag att man har ett prov med 1,0 gram <math>^{232}</math>Th. Provet innehåller då <math>6,022 \cdot 10^{23} \cdot 1,0/232</math> st kärnor = <math>2,6 \cdot 10^{21}</math> kärnor. | Avogadros tal <math>N_A = 6,022 \cdot 10^{23}</math> talar om hur många kärnor vi har per mol, där en mol är så många gram som formelvikten anger. Antag att man har ett prov med 1,0 gram <math>^{232}</math>Th. Provet innehåller då <math>6,022 \cdot 10^{23} \cdot 1,0/232</math> st kärnor = <math>2,6 \cdot 10^{21}</math> kärnor. | ||
| + | |||
| + | =<pp:latex>\alpha</pp:latex>-sönderfallet= | ||
''Mer material kommer'' | ''Mer material kommer'' | ||
Versionen från 6 december 2017 kl. 15.40
| Teori | Övningar |
Mål och innehåll
Innehåll:
- Kärnans beståndsdelar
- Kärnans storlek (Vid spridning av \displaystyle \:\alpha\:-partiklar …)
- Kärnans bindningsenergi (Massa som kan mätas …)
- Fission och fusion
- Solens fusionsprocess
- Naturlig radioaktivitet
- \displaystyle \:\alpha\:-sönderfallet
- \displaystyle \:\beta\:-sönderfallet
- \displaystyle \:\gamma\:-sönderfallet
- Kol 14-metoden
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Redogöra för kärnans beståndsdelar.
- Beräkna kärnans storlek.
- Beräkna en given kärnas bindningsenergi.
- Redogöra för fissionsprocessen.
- Redogöra för fusionsprocessen.
- Förklara hur fusionen i vår sol fungerar.
- Förklara vad som menas med naturlig radioaktivitet.
- Redogöra för \displaystyle \:\alpha\:-sönderfallet.
- Redogöra för \displaystyle \:\beta\:-sönderfallet.
- Redogöra för \displaystyle \:\gamma\:-sönderfallet.
- Redogöra för \displaystyle \:^{14}C-metoden
FÖRFATTARE: Göran Tranströmer & Lars-Erik Berg, KTH Fysik
Kärnan
Thomson upptäcker elektronen 1897 (men dess massa var ännu okänd) och har en modell för hur atomen var sammansatt.
Rutherford (Geiger, Marsden) undersöker hans ”plumpudding-modell” och finner att atomens positiva laddning (och därmed dess massa) är koncentrerad till ett mycket litet område, en kärna, med en utsträckning som är 1/10000 av atomens. Eftersom man förväntade sig mycket små spridningsvinklar (”A bullet through a sack of snowballs”) så blev resultatet av experimentet oerhört förvånande. Med Rutherfords egna ord
"It was quite the most incredible event that ever happened to me in my life. It was almost as incredible as if you had fired a 15-inch shell at a piece of tissue paper and it came back and hit you".
Rutherford föreslår (1920) p+ och e- för att bilda neutral partikel i kärnan, som behövs eftersom massan av antalet protoner är mindre än totala massan/2.
Denna lösning duger ej (enligt Heisenbergs osäkerhetsrelationer) Neutronen postuleras därför (1928) och hittas 1932 av Chadwick.
Kärnan består av protoner och neutroner, (som med ett gemensamt namn kallas för nukleoner) och deras totala antal är masstalet \displaystyle A
- Antalet protoner i kärnan anges av atomnumret \displaystyle Z
- Antalet neutroner i kärnan anges av \displaystyle N
- \displaystyle A = Z + N
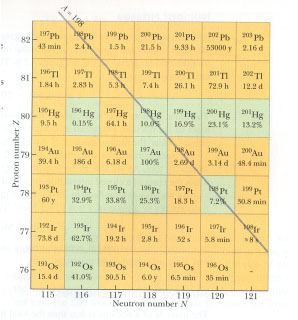
Kemiskt identiska ämnen men med olika massor, sänder ut olika radioaktiv strålning. Dessa ämnen med samma kemiska egenskaper kallas isotoper. De har olika atommassor (olika \displaystyle A) men samma atomnummer (samma antal protoner \displaystyle Z).
Nuklider med samma \displaystyle N, men olika \displaystyle Z, kallas isotoner medan nuklider med samma \displaystyle A kallas isobarer. Detta är icke att förväxla med värmelärans isobar som innebär samma tryck!
Av de ca 2000 kända nukliderna är bara 280 stabila, resten är radioaktiva, d.v.s. sönderfaller spontant. I naturen förekommer ett fåtal naturligt radioaktiva resten är framställda och kallas inducerat radioaktiva.
Vid spridning av \displaystyle \alpha -partiklar mot kärnor får man en avvikelse från Rutherfords teori för höga energier på a-partikeln (och lätta kärnor). Detta ger en möjlighet att bestämma kärnradien. Motsvarande försök har gjorts med elektroner (men det skedde senare eftersom det krävs hög energi för att ge elektronen en de Broglie-våglängd av en samma storlekordning som en kärnas diameter. Resultaten blev att kärnan kan (i en första approximation) betraktas som sfärisk med en radie \displaystyle R, som beror av masstalet \displaystyle A enligt
\displaystyle R = R_0A^{1/3}
där \displaystyle R_0 = 1{,}1\cdot10^{-15} \dots 1{,}4\cdot10^{-15}\, \textrm{m} och det lägre värdet är från elektronspridning och den högre från \displaystyle \alpha-partikelspridning.
Kärnans massa, som kan mätas med hög precision anges i atomic mass units som definieras som massan av \displaystyle 1/12\,\,^{12}\mathrm{C}-atom och har värdet
\displaystyle 1 \textrm{u} = 1,66056\cdot 10^{-27}\, \textrm{kg}
Det kan vara värt att lägga märke till att:
\displaystyle \textrm{u}\,c^2 =\displaystyle\frac{m_\mathrm{u}\,c^2}{e} =\displaystyle\frac{1{,}66056\cdot10^{-27}\:\mathrm{kg}\cdot(299792458\:\mathrm{ m/s})^2}{1{,}60217646\cdot10^{-19}\:\textrm{C}} = 931{,}494 \:\textrm{MeV}
och på samma sätt fås:
\displaystyle m_p\,c^2= 938{,}3 \textrm{ MeV}
\displaystyle m_n\,c^2= 939{,}6 \textrm{ MeV}
\displaystyle m_e\,c^2= 0{,}511 \textrm{ MeV}
Kärnans massa, \displaystyle M, är mindre än summan än de ingående protonernas och neutronernas sammanlagda massor. Denna massdefekt \displaystyle \Delta m svarar mot en energi \displaystyle E_{be} (>0), kärnans bindningsenergi.
\displaystyle E_{be}= \Sigma(m\,c^2)\, –\, M\,c^2 = \Delta m\,c^2
Om man tillför denna energi till kärnan kan man splittra den i dess beståndsdelar.
Om elektronernas bindningsenergier i atomen kan försummas kan \displaystyle E_{be} för en kärna med \displaystyle Z protoner och elektroner, och \displaystyle (A-Z) neutroner skrivas
\displaystyle E_{be} = Z m_p c^2 + (A-Z)m_n\,c^2 – (M - Z m_e)c^2
där \displaystyle M är atommassan (dvs kärna plus elektroner), \displaystyle m_p protonens massa, och \displaystyle m_e elektronens massa. Vi får alltså bindningsenergin som
\displaystyle E_{be} = Zm_p\,c^2 + (A-Z)m_n\,c^2 + Z m_e c^2 – M\,c^2
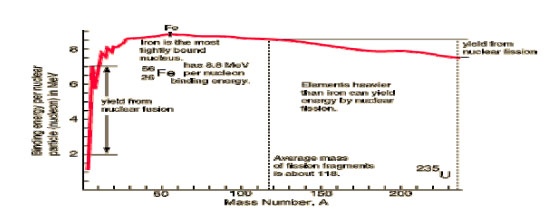
Bindningsenergin/nukleon blir då
\displaystyle \epsilon = \displaystyle\frac{E_{be}}{A}
där \displaystyle \varepsilon beror av A enligt figuren nedan.
Fission
En tung kärna kan splittras i två lättare kärnor, denna process kallas fission.
Om en kärna med masstalet \displaystyle A och atomnumret \displaystyle Z sönderfaller i två lika delar (ett möjligt sönderfall, men inte det vanligaste) ges viloenergin före av:
\displaystyle ZM_Hc^2 + (A-Z)m_nc^2 – A\varepsilon_A
och viloenergin efter av:
\displaystyle 2 \cdot \bigg( \displaystyle \frac{ZM_Hc^2}{2} + \displaystyle\frac{(A-Z)m_nc^2}{2} – \displaystyle\frac{A\varepsilon_{A/2}}{2} \bigg)
Förändringen i viloenergi är då
\displaystyle A\varepsilon_{A/2} - A\varepsilon_A > 0
Exempel
Hur stor blir då förändringen i viloenergi i ett konkret fall?
Antag \displaystyle A = 238 nukleoner, \displaystyle \epsilon_{A/2} = 8{,}5 \mbox{ MeV/nukleon} och \displaystyle \epsilon_{A} = 7{,}6 \mbox{ MeV/nukleon}.
Förändringen i viloenergi per kärna ges då enligt sambandet ovan av
\displaystyle A\epsilon_{A/2} - A\epsilon_A = 238\cdot8{,}5 - 238\cdot 7{,}6 \:\mathrm{ MeV/kärna} = 214{,}2 \:\mathrm{ MeV/kärna}.
Fusion
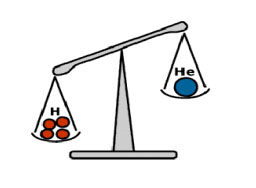
Vi har redan tidigare konstaterat att man kan utvinna energi genom att i en fusion slå samman två lätta kärnor till en tyngre. Solens fusionsreaktion grundar sig på nedanstående figur.
Därvid måste den repulsiva Coulombbarriären övervinnas för att kärnorna skall komma varandra så nära att den attraktiva kärnkraften som verkar på mycket korta avstånd skall ta överhanden. Man kan enkelt uppskatta hur stor Coulombbariären är för två kolliderande vätekärnor.
Exempel
Vilken (genomsnittlig) kinetisk energi måste vardera protonen ha om de skall övervinna repulsiva Coulombbarriären så att två protoner kan åstadkomma en fusion?
Lösning
Den kinetiska energin hos protonerna måste vara minst lika stor som den potentiella energin som måste överkommas
Potentiella energin mellan två laddningar \displaystyle q_1 och \displaystyle q_2 ges av
\displaystyle \displaystyle E = \frac{q_1 q_2}{4 \pi \varepsilon_0 r}
där \displaystyle r är avståndet melan laddningarna. Protonerna krockar när avståndet mellan dem är ungefär en femtometer, dvs \displaystyle 10^{-15} meter. Protonen har laddningen \displaystyle e, elementarladdningen (\displaystyle e \approx 1.60 \cdot 10^{-19} \text{ C}).
Vi får alltså att den potentiella energin mellan protonerna när de krockar är
\displaystyle \displaystyle E = \frac{q_1 q_2}{4 \pi \varepsilon_0 r} = \frac{e^2}{4 \pi \varepsilon_0 r} = \frac{(1.60 \cdot 10^{-19} \text{ C})^2}{4 \pi \cdot 8.85 \cdot 10^{-12} \text{ F/m} \cdot 10^{-15} \text{ m}} \approx 2.31 \cdot 10^{-13} \text{ J} \approx 1.44 \text{ MeV}.
Det här är den totala kinetiska energi som måste finnas i systemet av de två protonerna, så de måste vardera ha en kinetisk energi på 1.44/2 = 0.72 MeV = 720 keV.
Solen utstrålar (isotropt) energin \displaystyle 3{,}9 \cdot 10^{26}\,\textrm{J/s}. Fusionen i solens inre är en flerstegsprocess som innebär att väte omvandlas till helium. I det första steget kolliderar två vätekärnor (protoner) och bildar deuterium under utsändandet av en positron och en (elektron)neutrino enligt (Q-värdet är frigjort energi)
\displaystyle ^1\mbox{H}^{+} +\, ^{1}\mbox{H}^+ \longrightarrow \,^{2}\mbox{H}^{+} + e^+ + \nu_e (Q = 0,42 MeV)
(Därefter annihilerar förstås positronen med en elektron \displaystyle e^+ + e^- \longrightarrow \gamma + \gamma (Q = 1,02 MeV)) Detta är en sällsynt process, vanligen studsar bara protonerna (elastiskt) mot varandra, men en gång på \displaystyle 10^{26} kollisioner så bildas deuterium. Det är denna "flaskhals" som gör att solen brinner "långsamt" (men det bildas ändå deuterium i takten \displaystyle 10^{12}\,\textrm{kg/s} beroende på det stora antalet tillgängliga protoner).
När väl en deuteriumkärna har bildats så bildas snabbt en \displaystyle ^3\mbox{He}-kärna enligt
\displaystyle ^2\mbox{H}^+ +\, ^1\mbox{H}^+ \longrightarrow \,^3\mbox{He}^{2+} + \gamma (Q = 5,49 MeV)
Under i medeltal \displaystyle 10^5 år (Vad gör att processen tar så lång tid?) bildar två \displaystyle ^3\mbox{He}-kärnor en \displaystyle ^4\mbox{He}-kärna och två vätekärnor enligt
\displaystyle ^{3}\mbox{He}^{2+} +\, ^{3}\mbox{He}^{2+} \longrightarrow\, ^{4}\mbox{He}^{2+} +\, ^{1}\mbox{H}^{+} +\, ^{1}\mbox{H}^{+} (Q = 12,86 MeV)
och man kan summera solens totala p-p-cykel till
\displaystyle 2( \,^{1}\mbox{H}^{+} + \,^1\mbox{H}^+) \longrightarrow \,^4\mbox{He}^{2+} + 2(e^+ + n_e) + 2 \gamma och lägger man till fyra elektronmassor på vardera sidan kan man använda atommassorna och beräkna processens Q-värde,
\displaystyle Q = \Delta mc^2 = 4(1,007825)\mbox{u}c^2 – 4,002603 \mbox{u}c^2 = 0,028697 \mbox{u}c^2 = 26,7\,\textrm{MeV}
De båda neutrinopartiklarna bär iväg ungefär \displaystyle 0,5 \mbox{MeV} av denna energi från solen. När mängden väte har förbrunnit i solen (om ungefär \displaystyle 5\cdot 10^9 år) så räcker solens massa inte till för att starta en heliumcykel, utan solen slutar sin karriär som stjärna såsom en röd jätte. Andra massivare stjärnor kan fortsätta fusionsreaktionerna, dock kan man inte bilda fusionselement tyngre än \displaystyle ^{56}\mbox{Fe}. Element med masstal större än 56 tros dock bildas i supernovaexplosioner.
Den eleganta fusionsreaktionen i solen har man försökt kopiera på jorden men det faller på att reaktionen är för "långsam".
Lockande alternativa fusionsreaktioner som skulle kunna fungera är
\displaystyle ^2\mbox{H}^+ + \,^2\mbox{H}^+ \longrightarrow \,^3\mbox{He}^{2+} + n (Q = 3,27 MeV) \displaystyle ^2\mbox{H}^+ + \,^2\mbox{H}^+ \longrightarrow \,^3\mbox{H}^+ + \,^1\mbox{H}^+ (Q = 4,03 MeV) \displaystyle ^2\mbox{H}^+ + \,^3\mbox{H}^+ \longrightarrow \,^4\mbox{He}^{2+} + n (Q = 17,59 MeV)
Det finns tre kriterier som måste vara uppfyllda för att en framgångsrik (jordbaserad) fusionsreaktor skall fungera väl.
- Hög partikeltäthet (ett neutralt plasma) n
- Hög plasmatemperatur T<
- Lång inneslutningstid (t) av plasmat
Man kan visa att en fusionsreaktor som använder deuterium-tritium reaktionen måste uppfylla Lawsons kriterium att fusionens värme är större än förlusterna.
\displaystyle n\cdot \tau \ge 1,5 \cdot 10^{20} \textrm{s/m}^3
där \displaystyle \tau är kvoten mellan energiinnehållet och effektförlusten och \displaystyle n är densiteten.
Det finns olika sätt att försöka uppfylla Lawsonkriteriet. Ett annat sätt att skjuta med en kraftfull laser på tritium pellets för att erhålla fusion. Magnetisk inneslutning i en så kallad Tokamak där ITER är namnet på den senaste forskningsanläggningen som beräknas vara färdigbyggd år 2021.
Naturlig radioaktivitet
Det radioaktiva strålningen som upptäcktes av Becquerel (1896) kan innehålla tre olika komponenter
- \displaystyle \alpha-partiklar (som är heliumkärnor)
- \displaystyle \beta-partiklar (som är elektroner eller positroner)
- \displaystyle \gamma-partiklar (som är fotoner)
I sällsynta fall kan också neutroner och stora kärnfragment förekomma.
Antalet sönderfall från ett radioaktivt ämne avtar exponentiellt. Sannolikheten att en kärna skall sönderfalla på tiden \displaystyle dt (\displaystyle dt är så liten att \displaystyle dt \ll 1) är \displaystyle dt. Om det finns \displaystyle N radioaktiva kärnor vid tiden \displaystyle t, så sönderfaller antalet kärnor (därav minustecknet)
\displaystyle -\,\displaystyle\frac{dN}{dt} = N
med lösningen
\displaystyle N = N_0 e^{-\lambda t}
\displaystyle N_0 är antalet kärnor vid tiden \displaystyle t=0 och \displaystyle \lambda är sönderfallskonstanten som är olika för olika nuklider, Den beror av växelverkan mellan kärnan och de innersta elektronerna i atomen och är därför oberoende av om atomerna bildar en gas, vätska eller en fast kropp.
Om man känner halveringstiden, den tid det tar för \displaystyle N att halveras, kan man enkelt plocka fram konstanten \displaystyle \lambda.
\displaystyle N_{T/2} = \displaystyle\frac{N_0}{2}
\displaystyle N_{T/2} = N_0e^{-\lambda T_{1/2}}
Sätts dessa lika finner man
\displaystyle T_{1/2}=\displaystyle\frac{\ln 2}{\lambda}
Aktiviteten (decay rate) \displaystyle R, definieras som antalet sönderfall/tidsenhet och kan skrivas
\displaystyle R = -\,\displaystyle\frac{dN}{dt} = -\,\displaystyle\frac{d}{dt} N_0 e^{-\lambda t} = +\lambda N_0 e^{-\lambda t} = R_0 e^{-\lambda t}
vilket också kan skrivas
\displaystyle R = \lambda N
Aktiviteten mäts i enheten \displaystyle 1 \mbox{ Bq} (Becquerel) = 1 sönderfall/s. Tidigare användes enheten \displaystyle 1 \mbox{ Cu} (Curie) \displaystyle = 3,7\cdot10^7\:\mbox{Bq}.
Hur tar man reda på antalet kärnor i ett prov?
Avogadros tal \displaystyle N_A = 6,022 \cdot 10^{23} talar om hur många kärnor vi har per mol, där en mol är så många gram som formelvikten anger. Antag att man har ett prov med 1,0 gram \displaystyle ^{232}Th. Provet innehåller då \displaystyle 6,022 \cdot 10^{23} \cdot 1,0/232 st kärnor = \displaystyle 2,6 \cdot 10^{21} kärnor.
<pp:latex>\alpha</pp:latex>-sönderfallet
Mer material kommer