Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösning 5.2:1

FörberedandeFysik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
(Ny sida: Om <math>\pi^0</math>-partikeln har den totala energin E och rörelsemängden <math>p</math> och de båda fotonernas energier är <math>E_1</math> och <math>E_2</math> med rörelsemängde...)
Nuvarande version (13 december 2017 kl. 11.58) (redigera) (ogör)
 
Rad 1: Rad 1:
Om <math>\pi^0</math>-partikeln har den totala energin E och rörelsemängden
Om <math>\pi^0</math>-partikeln har den totala energin E och rörelsemängden
<math>p</math>
<math>p</math>
-
och de båda fotonernas energier är <math>E_1</math> och <math>E_2</math> med rörelsemängder <math>\mathbf{p_1}</math> och <math>\mathbf{p_2}</math> respektive, ger lagarna om energi och rörelsemängdens bevarande att
+
och de båda fotonernas energier är <math>E_1</math> och <math>E_2</math> med rörelsemängder <math>\mathbf{p_1}</math> och <math>\mathbf{p_2}</math> respektive, ger lagarna om energi och rörelsemängdens bevarande att
<math>E= E_1 + E_2</math>
<math>E= E_1 + E_2</math>

Nuvarande version

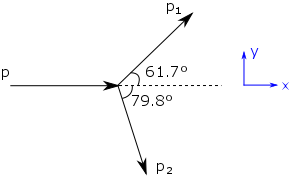
Om 0-partikeln har den totala energin E och rörelsemängden p och de båda fotonernas energier är E1 och E2 med rörelsemängder p1 och p2 respektive, ger lagarna om energi och rörelsemängdens bevarande att

E=E1+E2

p1sin617=p2sin798

p=p1cos617+p2cos798.

Bild:Ovn521SH012N.png

Rörelsemängden måse bevaras i både x- och y-led.

Vi har givet att E1=95MeV och eftersom fotoner är masslösa gäller att E1=cp1, vilket leder till att p1=95MeV/c. Med hjälp av E2=cp2 och p1sin617=p2sin798 får vi då att E2=85MeV och vi kan lätt räkna ut E och p från formlerna ovan. Vi får

E2=850MeV

E=1800MeV

p=601MeV/c

som slutligen med energitriangeln ger

E0=E2−p2c2=1697MeV 

Den här artikeln är hämtad från http://wiki.math.se/wikis/forberedandefysik/index.php/L%C3%B6sning_5.2:1