FörberedandeFysik

Versionen från 9 januari 2018 kl. 16.19 (redigera) Louwah (Diskussion | bidrag) ← Gå till föregående ändring		Versionen från 9 januari 2018 kl. 16.25 (redigera) (ogör) Louwah (Diskussion | bidrag) Gå till nästa ändring →
Rad 131:		Rad 131:
-	=Cirkulär rörelse med konstant hastighet=	+	=Cirkulär rörelse med konstant fart=
-	Här behandlas en partikel som rör sig i en cirkelbana med konstant hastighet:	+	Här behandlas en partikel som rör sig i en cirkelbana med konstant fart:
	[[Bild:cirkelbana.jpg|center]]		[[Bild:cirkelbana.jpg|center]]
-	Partikeln har en konstant hastighet <math>v</math>.<br\>	+	Partikeln har en konstant fart <math>v</math>.<br\>
	Cirkeln har en radie <math>r</math>.<br\>		Cirkeln har en radie <math>r</math>.<br\>
	Som baslinje väljer vi radien då tiden <math>t=0</math>.<br\>		Som baslinje väljer vi radien då tiden <math>t=0</math>.<br\>
Rad 148:		Rad 148:
-	Pga konstant hastighet är partikelns hastighet <math>v=\frac{s}{t}</math>.	+	Pga konstant fart är partikelns fart <math>v=\frac{s}{t}</math>.

---

Versionen från 9 januari 2018 kl. 16.25

Teori

Övningar

FÖRFATTARE: Ian Cohen, KTH Mekanik

Rörelsebeskrivning i koordinatsystem

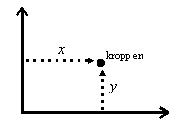
När en kropp betraktas som en partikel som inte rör sig längs en bana, utan i ett plan, räcker det inte med en koordinat, t.ex. \displaystyle s som anger kroppens läge vid en viss tid \displaystyle t. Man behöver två koordinater då ett plan har två dimensioner: Man kan beskriva kroppens läge t.ex. med hjälp av kartesiska koordinater \displaystyle x och \displaystyle y som på bilden nedan. Det är även möjligt att välja andra koordinatsystem vars behandling dock ligger utanför kursens ramar.

För beskrivningen av kroppens rörelse är det fördelaktigt att använda vektorer, se avsnitt 2.2 om Elementär vektoralgebra.

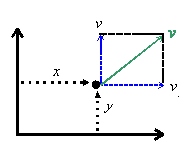
Antag att kroppen har en hastighet \displaystyle v i ett visst ögonblick. Då kan man dela upp denna hastighet i två delar som kallas komposanter: En \displaystyle v_x pekar längs \displaystyle x-riktningen och en \displaystyle v_y pekar längs \displaystyle y-riktningen. \displaystyle v_x kallas hastighetens \displaystyle x-komponent och \displaystyle v_y kallas hastighetens \displaystyle y-komponent. De kan vara positiva såväl som negativa (Varför?).

Om hastigheten är konstant och kroppen startar sin rörelse från origo vid \displaystyle t=0, erhålls:

\displaystyle x=v_xt
\displaystyle y=v_yt

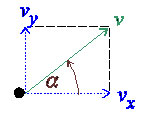
Om \displaystyle \alpha är hastighetens vinkel mot \displaystyle x-riktningen:

erhålls

\displaystyle v_x=v\cos\alpha
\displaystyle v_y=v\sin\alpha

Kaströrelse

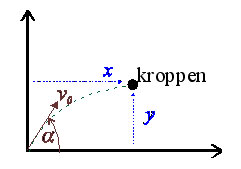
En viktig tillämpning av teorin om tvådimensionell rörelse är kaströrelse. En kropp som kan betraktas som en partikel kastas från en punkt med starthastigheten \displaystyle v_0. Välj startpunkten som origo och mät tiden från \displaystyle 0. Välj \displaystyle y-axeln positiva riktning uppåt och \displaystyle x-axeln i samma riktning som \displaystyle x-komponenten av hastigheten. Låt \displaystyle \alpha vara starthastighetens vinkel med \displaystyle x-axeln. Då får vi följande figur:

Då vi bortser från luftmotståndet har kroppen en acceleration \displaystyle g i den negativa \displaystyle y-riktningen. I \displaystyle x-riktningen är accelerationen lika med noll.

I \displaystyle x-riktningen är hastigheten \displaystyle v_x=v_{0x} och konstant.
Förflyttningen i \displaystyle x-riktningen är \displaystyle x=v_{0x}t.
Här är \displaystyle v_0x=v_0\cos\alpha

I \displaystyle y-riktningen kan vi tillämpa teorin för konstant acceleration där accelerationen är \displaystyle -g.

Således: \displaystyle v_y=v_{0y}-gt
\displaystyle y=v_{0y}t-\frac{1}{2}gt^2
Här är \displaystyle v_{0y}=v_0\sin\alpha

Om vi använder sambanden \displaystyle x=v_{0x}t och \displaystyle y=v_{0y}t-\frac{1}{2}gt^2 som vi härledde ovan och eliminerar tidsvariabeln \displaystyle t, får vi en relation mellan \displaystyle x och \displaystyle y för kroppens bana som visar sig vara en parabel.

Kroklinjig rörelse

Alla exempel vi behandlat hittills har haft konstant acceleration som betyder att såväl storleken som riktningen av accelerationen är konstant. En bil t.ex. som kör med konstant fart men längs en kurvig väg har inte en konstant acceleration då riktningen är variabel.

För att undersöka fallet då accelerationen inte är konstant är man tvungen att behandla rörelsebeskrivningen mer matematiskt.

Längs en bestämd bana med förflyttningen \displaystyle s gäller för hastigheten \displaystyle v och accelerationen \displaystyle a enligt avsnitt 3.1 om Linjebunden rörelse:

\displaystyle v=\frac{ds}{dt}

\displaystyle a=\frac{dv}{dt}

För rörelse i planet då vi använder \displaystyle x- och \displaystyle y-koordinater följer av det följande definitioner:

Hastighet i \displaystyle x-riktning \displaystyle v_x=\frac{dx}{dt}

Hastighet i \displaystyle y-riktning \displaystyle v_y=\frac{dy}{dt}

Acceleration i \displaystyle x-riktning \displaystyle a_x=\frac{dv_x}{dt}

Acceleration i \displaystyle y-riktning \displaystyle a_y=\frac{dv_y}{dt}

Både hastighet och acceleration är vektorer med komponenter \displaystyle \frac{dx}{dt} och \displaystyle \frac{dy}{dt} respektive
\displaystyle \frac{dv_x}{dt} och \displaystyle \frac{dv_y}{dt}

Anmärkningar:

1. Att hastighet och acceleration är vektorer innebär att de kan ha komponenter i vilken riktning som helst. T.ex. är komponenten av hastigheten \displaystyle v i en riktning som bildar en vinkel \displaystyle \alpha mot hastigheten, alltid \displaystyle v\cos\alpha.

2. För att bestämma hastigheten utifrån accelerationen brukar det krävas integration eller lösning av en differentialekvation, vilket dock inte ingår i denna kurs.

Cirkulär rörelse med konstant fart

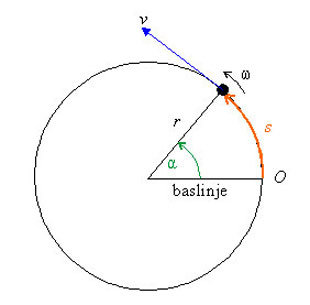
Här behandlas en partikel som rör sig i en cirkelbana med konstant fart:

Partikeln har en konstant fart \displaystyle v.
Cirkeln har en radie \displaystyle r.
Som baslinje väljer vi radien då tiden \displaystyle t=0.
I figuren antar vi att en tid \displaystyle t har gått sedan partikeln passerat eller startat vid origo \displaystyle O.
Radien bildar en vinkel \displaystyle \alpha med baslinjen.
Partikeln har förflyttat sig med \displaystyle s från origo.

I geometrin bevisar man att \displaystyle s=\alpha \cdot r.
T.ex. blir vid ett helt varv \displaystyle s = cirkelns omkrets \displaystyle = 2\pi \cdot r.

Pga konstant fart är partikelns fart \displaystyle v=\frac{s}{t}.

Vinkelhastighet, period och frekvens

En annan sak än partikelns hastighet är vinkelhastigheten \displaystyle \omega som definieras som vinkeln \displaystyle \alpha:s ändring med tiden dvs:

\displaystyle \omega =\frac{vinkeländring}{tidsintervall}=\frac{\alpha}{t}.

Vid variabel hastighet, är vinkelhastigheten \displaystyle \omega =\frac{d\alpha}{dt} vilket inte behandlas i denna kurs.

De tre sambanden \displaystyle s=\alpha \cdot r , \displaystyle v=\frac{s}{t} och \displaystyle \omega =\frac{\alpha}{t} ger \displaystyle v=\omega \cdot r.

Partikelns acceleration är en vektor och är inte konstant. I varje ögonblick är partikelns acceleration i hastighetens riktning noll eftersom hastigheten är konstant. Men det kan visas att partikeln har en acceleration i riktning mot cirkelns centrum vinkelrät mot hastigheten. Denna acceleration kallas centripetalacceleration och har värdet \displaystyle \frac{v^2}{r}.

Eftersom centripetalaccelerationen alltid är riktad mot cirkelns centrum fast den har en konstant storlek, ändras riktningen hela tiden varför accelerationsvektorn, inte är konstant.

Det är lätt att se att centripetalacceleration också kan skrivas som \displaystyle \omega ^2r eftersom \displaystyle \frac{v^2}{r}=\omega ^2r.

Tiden det tar för partikeln att fullborda ett varv kallas perioden \displaystyle T.

Eftersom cirkelns omkrets är \displaystyle 2\pi r gäller \displaystyle T=\frac{2\pi r}{v}=\frac{2\pi r}{\omega r}=\frac{2\pi}{\omega}

Frekvensen \displaystyle f anger hur många varv partikeln tillryggalägger per sekund.

Eftersom \displaystyle f=1/T gäller \displaystyle f=\frac{\omega}{2\pi}.

Att \displaystyle f=1/T är lätt att inse om vi betraktar exemplet \displaystyle T=1/3 sekunder vilket innebär att partikeln hinner med tre varv under en sekund.

Harmonisk svängningsrörelse

En partikel som svänger fram och tillbaka utför en svängningsrörelse. Den viktigaste svängningsrörelsen är harmonisk svängningsrörelse vars teori bildar grunden för många andra svängningsrörelser i fysiken.

Det enklaste sättet att presentera harmonisk svängningsrörelse är att tillämpa det som sades ovan om cirkulär rörelse med konstant hastighet.

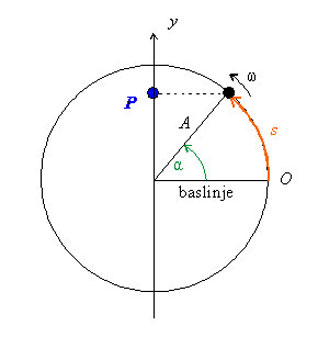
Vi inför i förra bilden en \displaystyle y-axel vinkelrät mot baslinjen. En punkt \displaystyle P som har samma \displaystyle y-koordinat som den roterande partikeln på cirkeln, kallas partikelns projektion på \displaystyle y-axeln. Denna punkt \displaystyle P utför en harmonisk svängningsrörelse. Cirkelns radie betecknas nu med bokstaven \displaystyle A:

Viktigast är att inse att punkten \displaystyle P rör sig fram och tillbaka längs \displaystyle y-axel kring cirkelns centrum.

Man brukar kalla cirkelns radie för svängningens amplitud \displaystyle A.

Svängningens period och frekvens är samma som förut.

Elementär trigonometri ger \displaystyle y=A\sin a=A\sin\omega t.

Man kan visa att \displaystyle P:s acceleration \displaystyle a är \displaystyle a=-\omega ^2y.

För mer teori hänvisas till HEUREKA! Fysik kurs B, första delen av kapitel 6, avsnitt 4.