Lösning 3.6:2
FörberedandeFysik
| Rad 1: | Rad 1: | ||
a) Om nollnivån sätts vid utgångsläget eftersom utgångshastigheten då är noll, är den totala energin noll. | a) Om nollnivån sätts vid utgångsläget eftersom utgångshastigheten då är noll, är den totala energin noll. | ||
| - | Vid lägsta läget har kulan den totala energin <math>\frac{1}{2}mv^2 - mg(40 cm)</math> där <math>m</math> är kulans massa. | + | Vid lägsta läget har kulan den totala energin <math>\frac{1}{2}mv^2 - mg(40 \,\mathrm{cm})</math> där <math>m</math> är kulans massa. |
| - | <math>\Rightarrow \frac{1}{2}mv^2 - mg( | + | <math>\Rightarrow \frac{1}{2}mv^2 - mg(40 \,\mathrm{cm}) = 0 \Rightarrow v^2 = 2g(40 \,\mathrm{cm})=8(\,\mathrm{m/s})^2 \Rightarrow v=2\sqrt{2} \,\mathrm{m/s} = 2,83 \,\mathrm{m/s}</math> |
| - | b) Centripetalaccelerationen är <math>\frac{v^2}{radie} = \frac{8(m/s)^2}{ | + | b) Centripetalaccelerationen är <math>\frac{v^2}{radie} = \frac{8(\,\mathrm{m/s})^2}{40 \,\mathrm{cm}} = 20 \,\mathrm{m/s}^2</math> |
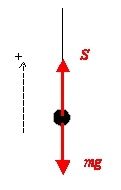
c) Kraftsumman med positiv uppåt är <math>S - mg</math>. | c) Kraftsumman med positiv uppåt är <math>S - mg</math>. | ||
| - | Kraftekvationen med positiv uppåt ger <math>S - mg = m( | + | Kraftekvationen med positiv uppåt ger <math>S - mg = m(20 \,\mathrm{m/s}^2) \Rightarrow S = 150 \,\mathrm{N}</math> |
[[Bild:losning_3_6_2.jpg]] | [[Bild:losning_3_6_2.jpg]] | ||
Nuvarande version
a) Om nollnivån sätts vid utgångsläget eftersom utgångshastigheten då är noll, är den totala energin noll.
Vid lägsta läget har kulan den totala energin \displaystyle \frac{1}{2}mv^2 - mg(40 \,\mathrm{cm}) där \displaystyle m är kulans massa.
\displaystyle \Rightarrow \frac{1}{2}mv^2 - mg(40 \,\mathrm{cm}) = 0 \Rightarrow v^2 = 2g(40 \,\mathrm{cm})=8(\,\mathrm{m/s})^2 \Rightarrow v=2\sqrt{2} \,\mathrm{m/s} = 2,83 \,\mathrm{m/s}
b) Centripetalaccelerationen är \displaystyle \frac{v^2}{radie} = \frac{8(\,\mathrm{m/s})^2}{40 \,\mathrm{cm}} = 20 \,\mathrm{m/s}^2
c) Kraftsumman med positiv uppåt är \displaystyle S - mg.
Kraftekvationen med positiv uppåt ger \displaystyle S - mg = m(20 \,\mathrm{m/s}^2) \Rightarrow S = 150 \,\mathrm{N}