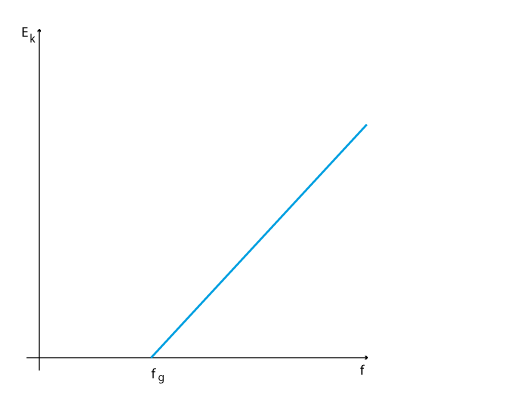FörberedandeFysik

Teori

Övningar

FÖRFATTARE: Göran Tranströmer & Lars-Erik Berg, KTH Fysik. EDITERARE: Johan Laine, Johanna Skarpman Munter

Ljusets partikelegenskaper

I slutet av 1800-talet dominerade uppfattningen att ljus är vågor. Att ljus har diffraktionsegenskaper var känt sedan länge, så när Maxwell visade att ljus är vågor som har sitt ursprung från elektromagnetisk strålning var det ingen som tvivlade på ljusets vågegenskaper. (Diffraktion är en vågegenskap som handlar om vågors egenskaper att sprida sig och böja sig runt hörn. Se exempelvis avsnitt 4.5 eller Wikipedia.)

Många fysiker avfärdade därför Max Planck när han försökte argumentera för att ljus bara kan avges och tas upp i vissa bestämda mängder, så kallade kvanta, i ett försök att förklara svartkroppsstrålning. Han fann att den energi som finns i ljus alltid är en multipel av en lägsta möjlig energikvanta som ges av

\displaystyle E=hf

där \displaystyle f är vågens frekvens. Konstanten som binder samman frekvensen med energin kallas för Plancks konstant och har värdet

\displaystyle h=6,626069\cdot 10^{-34} \textrm{ Js} \approx 4,136\cdot10^{-15} \textrm{ eV s} \,.

Idag är det ingen som tvivlar på att modellen stämmer, men tanken var väldigt kontroversiell och hårt motarbetad under 1900-talets början. Dessa ljuskvanta är de partiklar som vi nu kallar fotoner.

Vi har sambandet \displaystyle f=c/\lambda där \displaystyle \lambda är våglängden, \displaystyle f är frekvensen och \displaystyle c är ljusets hastighet. Det innebär att vi kan skriva om Plancks formel som

\displaystyle E=\displaystyle\frac{hc}{\lambda}.

Relationen \displaystyle hc dyker upp så ofta i dessa beräkningar att värdet kan vara bra att notera

\displaystyle hc \approx 1,986445\cdot 10^{-25} \textrm{ Jm} \approx 1240 \textrm{ eV nm}.

En annan konstant som ofta dyker upp i dessa sammanhang är \displaystyle \displaystyle\frac{h}{2\pi}. Den brukar kallas Diracs konstant eller bara "h-streck".

\displaystyle \hbar=\displaystyle\frac{h}{2\pi} \approx 1,054572 \cdot 10^{-34} \textrm{ Js} \approx 6,58 \cdot 10^{-16} \textrm{ eV s}.

Om vi kombinerar Plancks formel med Einsteins resultat att även ljus har rörelsemängd som beskrivs av \displaystyle p=E/c får vi att

\displaystyle p=\displaystyle\frac{h}{\lambda}=\displaystyle\frac{hf}{c} \,.

de Broglies hypoteser

Att ljus har diffraktionsegenskaper kan bara förklaras med vågteori. Men fenomen som fotoelektriska effekten och Comptoneffekten går däremot bara att beskriva om ljus består av partiklar. Denna dualism var svårsmält för många under början av 1920-talet, även om fler och fler av fysikerna började acceptera detta. Knappt hade chocken lagt sig när en man vid namn de Broglie 1924 i sin doktorsavhandling presenterade sitt förslag om att all materia har vågegenskaper förutom de självklara partikelegenskaperna. Denna våg-partikeldualism för materia med massa var ett avgörande genombrott för kvantfysiken. Han tog fram två hypoteser som 1927 bekräftades experimentellt av Davisson-Germers och George Thomsons respektive experiment. Oberoende av varandra bevisade de att även elektroner ger diffraktionsmönster och alltså måste bestå av vågrörelser.

Einstein hade föreslagit att man kan associera rörelsemängd till ljus enligt \displaystyle p=h/\lambda. de Broglie föreslår att också det omvända gäller: att man till varje materiell partikel med rörelsemängden \displaystyle p kan associera en våglängd enligt

\displaystyle \lambda=\displaystyle\frac{h}{p}

där \displaystyle h är Plancks konstant. Denna våglängd brukar kallas för de Broglie-våglängd. Det innebär att alla föremål, från bilar till elektroner har vågegenskaper! Dock är våglängden för de flesta föremål så liten att det är omöjligt att detektera några sådana egenskaper hos vardagliga föremål. Man brukar säga att föremål uppfattas som en våg då våglängden är i samma storleksordning som observatören.

de Broglies hypotes om materievågor har bekräftats experimentellt. Bland annat genom det berömda dubbelspalt-experimentet där det visades att elektroner både uppför sig som en våg och som en partikel, beroende på hur man mäter.

Vidare föreslog de Broglie nedanstående samband som kopplade samman den kinetiska energin med frekvensen

\displaystyle f=\displaystyle\frac{E_k}{h}

där \displaystyle f är frekvensen på materievågen och \displaystyle E_k är partikelns kinetiska energi.

Notera nu att sambandet \displaystyle f\lambda=v återigen ger \displaystyle E=vp, men \displaystyle v är i regel inte partikelns hastighet, utan våghastigheten, som alltså inte är samma sak som partikelns hastighet.

Braggs lag

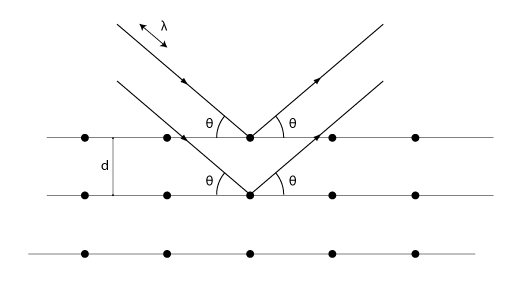
Om man låter röntgenstrålar träffa en kristallstruktur kommer några vågor träffa atomkärnorna och därmed reflekteras. Eftersom våglängden för röntgenstrålar är i samma storleksordning som avståndet mellan atomkärnorna hos kristaller kommer vi lätt kunna uppfatta strålarnas vågegenskaper. En typisk vågegenskap är interferens (se avsnitt 4.5). Då vi skickar strålarna mot kristallen kommer olika strålar reflekteras av olika lager i kristallstrukturen. Bilden nedan illustrerar detta. Vid vissa infallsvinklar och våglängder kommer vi få en reflekterad våg som har betydligt högre intensitet än den vi skickar in på grund av konstruktiv interferens.

När Bragg-villkoret

\displaystyle 2d\sin{\theta}=m\lambda

är uppfyllt kommer vi få konstruktiv interferens. Det innebär att vägskillnaden (\displaystyle 2dsin{\theta}) mellan strålarna ska vara ett heltal gånger våglängden för att ge konstruktiv interferens. Här är \displaystyle d avståndet mellan atomlagren, \displaystyle \lambda är strålningens våglängd och \displaystyle m är de olika maxima man får. Det första maximumet får vi då \displaystyle m=1, det andra vid \displaystyle m=2 och så vidare. Kom ihåg att infallsvinkeln alltid är lika med reflexionsvinkeln vid reflexion!

Förutsatt att man känner till våglängden kan man på detta sätt bestämma avståndet mellan atomlagren. Braggs lag är därför ett viktigt hjälpmedel inom den del av fysiken som undersöker vad olika kristallina material har för inre struktur.

Röntgenstrålning

Elektromagnetiska vågor med våglängd runt \displaystyle 0,01-10 \textrm{ nm} kallas för röntgenstrålning. Wilhelm Röntgen laborerade med dessa strålar och fann att mänsklig vävnad i stort sett var genomskinlig för dessa våglängder. Genom att detektera hur mycket strålning som går igenom vävnaden kan man därför få en mycket bra bild av kroppens insida.

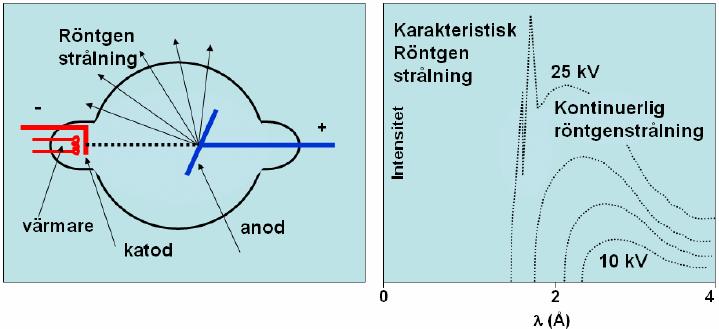
Vi kan skapa röntgenstrålar med hjälp av ett så kallat röntgenrör (se figur nedan till vänster). Där genereras elektroner vid en katod (negativ elektrod) som sedan accelereras mot en anod (positiv elektrod) med hjälp av en spänning. Elektronerna får den kinetiska energin \displaystyle E_k = eU, där \displaystyle e är elementarladdningen och \displaystyle U är spänningen. Då elektronerna träffar anoden avges fotoner.

Strålningsspektrat ovan till höger är genererat för spänningar mellan \displaystyle 10 och \displaystyle 25 \textrm{ keV}, där de olika kurvorna motsvarar olika spänningar. Spektrat visar intensiteten som funktion av våglängden på röntgenstrålningen. I grafen för den högsta spänningen ser vi strålning som har uppkommit på två olika sätt. De två spetsiga topparna i spektrat i den första kurvan står för den så kallade karakteristiska strålningen eftersom den är olika om man har olika metaller i anoden. Den uppkommer då elektroner krockar med atomer i anoden så att atomerna exciteras. Det betyder att elektroner i anodatomen flyttas till en högre energinivå. När den exciterade elektronen sedan återvänder till den ursprungliga energinivån skickas en foton ut. Excitation från de två energinivåer som är närmast kärnan är de energihopp som kan ge upphov till röntgenstrålning och det är därför vi ser två toppar. Olika ämnen skickar ut olika energirika fotoner då den exciterade elektronen återvänder till sin ursprungliga energinivå, därför kommer topparna vara placerade vid olika våglängder för olika ämnen. Anledningen till att vi bara ser detta fenomen för den högsta spänningen i figuren är för att energin måste vara tillräckligt hög för att atomernas ska exciteras.

Vid alla olika spänningar ser vi däremot ett kontinuerligt spektrum. Då laddade partiklar bromsas kraftigt skapas högenergetisk strålning. Strålningen som vi ser i det kontinuerliga spektrat kallas därför bromsstrålning. Den är helt oberoende av vilken metall anoden består av. Däremot varierar den beroende på vilken spänning elektronerna accelereras med.

Röntgenstrålningen med den högsta energin uppkommer då all kinetisk energi från en elektron överförs till en foton. Denna högsta energi motsvaras av den kortaste våglängden \displaystyle \lambda_{min} (se Plancks formel).

Exempel - kortaste våglängden

Vi kan beräkna den kortaste våglängden för till exempel \displaystyle 25 \textrm{ kV}-spektrat. Genom att sätta den kinetiska energin för elektronen \displaystyle E_{elektron} = eU = 25 \textrm{ keV} lika med energin för en foton \displaystyle E_{foton} = \displaystyle\frac{hc}{\lambda} kan vi finna denna minsta våglängd \displaystyle \lambda_{min}.

\displaystyle \lambda_{min} = \displaystyle\frac{hc}{25 \textrm{ keV}} \approx 0,050 \textrm{ nm}

Att denna minsta våglängd existerar innebär att elektroner inte kan kombinera sina energier för att skicka iväg fotoner med ännu högre energi än den maximala kinetiska energin hos en elektron. Detta är en första bekräftelse av många som vi kommer se framöver på att hypotesen om det kvantiserade ljuset stämmer.

Fotoelektriska effekten

När vissa material belyses med elektromagnetisk strålning avger materialet elektroner. Detta kan sägas vara motsatsen till vad som händer då röntgenstrålning skapas. Effekten kallas fotoelektrisk effekt. Många fysiker på 1800-talet noterade att hade man för lång våglängd avgav materialet inga elektroner alls, oavsett hur hög intensitet man hade på ljuset. Om man däremot gick under ett visst tröskelvärde på våglängden började materialet avge elektroner. Det märkliga var att elektronerna inte fick högre energi om man höjde ljusets intensitet, det var bara våglängden som påverkade elektronernas kinetiska energi. Detta stred mot den då rådande synen att ljus bara hade vågegenskaper och det hela sågs som en oförklarad paradox inom fysiken.

Lösningen kom 1905 med Einsteins banbrytande arbete "On a Heuristic Viewpoint Concerning the Production and Transformation of Light" som sedermera gav Einstein Nobelpriset i fysik 1921 (inte relativitetsteorin!). Einstein tog till sig Plancks idé att ljus enbart uppträder i vissa strålningskvanta i form av fotoner. Fotonen rör sig med ljushastigheten \displaystyle c och absorberas i sin helhet av en elektron i en metallyta som därigenom får en kinetisk energi \displaystyle E_k.

Formeln som beskriver fotoelektriska effekten är

\displaystyle hf=\Phi+E_k

där \displaystyle f är ljusvågens frekvens, \displaystyle \Phi är utträdesarbetet (arbetet som krävs för att tvinga iväg en elektron) som är en materialkonstant och \displaystyle E_k är den kinetiska energi som elektronen får om \displaystyle hf \ge \Phi. Om fotonens energi \displaystyle hf är lägre än utträdesarbetet \displaystyle \Phi avges ingen elektron alls. I annat fall går fotonens energi åt till att frigöra elektronen och \displaystyle hf-\Phi blir elektronens kinetiska energi.

Teorin mötte hårt motstånd eftersom detta stred mot Maxwells lagar om elektromagnetism och uppfattningen att energi kan anta hur små värden som helst, så kallad oändlig delbarhet. 1914 visade R.A. Millikan med sin försöksuppställning med en fotodetektor att Einstein hade rätt. Teorin förutspår att man vid en viss gränsfrekvens \displaystyle f_g ska kunna detektera fria elektroner och att energin sedan stiger linjärt med ökande frekvens enligt detta linjära samband där lutningen är Plancks konstant.

\displaystyle E_k=hf-\Phi

Diagrammet nedan visar hur resultaten från ett sådant experiment kan se ut.

Trots att teorin bekräftades i och med Millikans experiment fortsatte kritiken mot Einstein eftersom det ansågs motsäga ljusets vågegenskaper som ju också var experimentellt bekräftade.

Comptoneffekten

Arthur H Compton utförde 1923 ett experiment där han lät en röntgenstråle träffa kolatomer i olika infallsvinklar. Hans experiment påvisade den fotoelektriska effekten och visade på fotonernas dubbelnatur som både partiklar och vågrörelser.

Comptons spridningslag

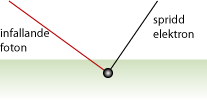
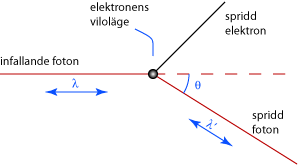
När en foton med tillräckligt hög energi träffar en bunden elektron kommer den att stöta loss elektronen och själv fortsätta med en annan våglängd i en ny riktning (se bilden nedan). Detta visar tydligt att fotonen i detta fall beter sig som en partikel. Beskrivningen av denna effekt gav Compton och hans kollega C.T.R. Wilson Nobelpriset i fysik 1927.

Comptons spridningslag lyder

\displaystyle \lambda' - \lambda = \displaystyle\frac{h}{m_e c} ( 1 - \cos \theta )

där \displaystyle \theta är fotonens spridningsvinkel, \displaystyle \lambda är våglängden hos den infallande fotonen och \displaystyle \lambda ' är våglängden hos den utgående fotonen. Relationen \displaystyle \displaystyle\frac{h}{m_e c} är konstant och brukar kallas Comptonvåglängden \displaystyle \lambda_c,

\displaystyle \lambda_c = \displaystyle\frac{h}{m_e c} \approx 0,00243 \textrm{ nm}.

Parbildning

Parbildning är ytterligare ett exempel på när en foton växelverkar med materia som en partikel.

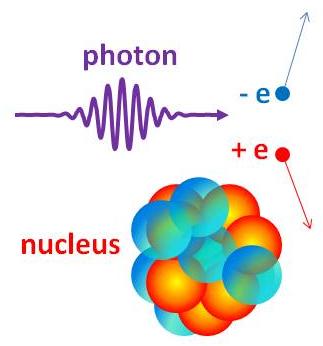
En energirik foton kan sönderfalla i ett elektron-positronpar (en positron är elektronens antipartikel och har istället positiv laddning) under parbildning i närheten av en tung kärna.

Fotonen har energin \displaystyle E_\gamma och rörelsemängden \displaystyle p_\gamma. Principen om energin och rörelsemängdens bevarande ger sambanden

\displaystyle E_\gamma = E_{e-} + E_{e+} = \{\textrm{energitriangeln ger}\} = \sqrt{(p_{e-}\, c)^2 + (m_e\, c^2)^2} + \sqrt{(p_{e+}\, c)^2 + (m_e\, c^2)^2 }

\displaystyle p_\gamma = p_{e-} + p_{e+}

där \displaystyle E och \displaystyle p står för energi respektive rörelsemängd. Indexen \displaystyle \gamma, \displaystyle e- och \displaystyle e+ står i sin tur för fotonen, elektronen och positronen.

Vi multiplicerar vänsterledet i ekvatonen för rörelsemängdens bevarande med \displaystyle c. Detta ger (i fotonens rörelseriktning)

\displaystyle p_\gamma\, c = E_\gamma

men enligt ekvationen för energins bevarande ovan gäller

\displaystyle E_\gamma = \sqrt{(p_{e-}\, c)^2 + (m_e\, c^2)^2} + \sqrt{(p_{e+}\, c)^2 + (m_e\, c^2)^2 } \,> \, p_{e-} c + p_{e+} c

Denna strikta olikhet gäller alltid (den intresserade läsaren kan läsa om triangelolikheten på Wikipedia). Vi kan därmed dra slutsatsen att det inte går att uppfylla villkoren om energin och rörelsemängens bevarande utan att en fjärde part medverkar i processen. Denna fjärde part kan bestå av en tung kärna som genom sin närvaro kan överta den överflödiga rörelsemängden. Om kärnan är tung så övertar den en mycket liten del av energin i processen.

Exempel

Vi tittar på en foton som i närhet av en kärna sönderfaller i en elektron och en positron genom parbildning.

Låt den infallande fotonen ha energin \displaystyle 3,0\textrm{ MeV}. Motsvarande rörelsemängd blir då \displaystyle 3,0 \textrm{ MeV/c}. Elektron-positronenergierna kan anta godtyckliga värden (de måste förstås vara minst elektronens viloenergi \displaystyle E_0 = 0,511 \textrm{ MeV}) så länge som totala energin är bevarad. Låt till exempel \displaystyle E_{e-} = 1,80 \textrm{ MeV}. Enligt principen om energins bevarande måste då \displaystyle E_{e+} = 1,20 \textrm{ MeV}. Vi löser ut motsvarande rörelsemängder från energitriangeln (\displaystyle E^2 = p^2 c^2 + E^2_0)

\displaystyle p_{e-} = \sqrt{\displaystyle\frac{E^2_{e-}}{c^2}-\displaystyle\frac{E^2_0}{c^2}} = \sqrt{\displaystyle\frac{(1,80 \textrm{ MeV})^2}{c^2}-\displaystyle\frac{(0,511 \textrm{ MeV})^2}{c^2}} \approx 1,73 \textrm{ MeV/c}

och på samma sätt för positronen

\displaystyle p_{e+} = \sqrt{\displaystyle\frac{(1,20 \textrm{ MeV})^2}{c^2}-\displaystyle\frac{(0,511 \textrm{ MeV})^2}{c^2}} \approx 1,09 \textrm{ MeV/c}.

Rörelsemängden som måste tas upp av kärnan blir därför enligt principen om rörelsemängdens bevarande

\displaystyle p_\gamma - p_{e-} - p_{e+} = 3,0 \textrm{ MeV/c} -\, 1,73 \textrm{ MeV/c} -\, 1,09 \textrm{ MeV/c} = 0,18 \textrm{ MeV/c}.

Eftersom kärnan är tung och troligtvis inte får så hög hastighet så antar vi att vi kan räkna orelativistiskt (men det måste vi förstås kontrollera på slutet). Rörelseenergin \displaystyle E_k för kärnan blir då

\displaystyle E_k = \displaystyle\frac{p^2}{2m} = \displaystyle\frac{(0,18 \textrm{ (MeV/c)})^2 }{2m} = 0,0324 \textrm{ (MeV)}^2\, /2mc^2

där \displaystyle m är den tunga kärnans massa. För att få en uppfattning om \displaystyle E_k låter vi kärnan vara den lättaste tänkbara det vill säga en proton med \displaystyle mc^2 = 938,3 \textrm{ MeV}. Då blir \displaystyle E_k = 0.000\, 017 \textrm{ MeV} = 17 \textrm{ eV}, vilket vi lätt kan försumma och vårt antagande ovan var riktigt. Kärnan övertar alltså inte någon betydande del av processens energi.

Mer material kommer