FörberedandeFysik

Teori

Övningar

Växelström

Det finns ett antal sätt att överföra elektisk energi på. Vanligast är att föra över den i form av en- eller trefas växelström.

I vårt dagliga liv använder vi oss av utrustning som drivs med växelström. Med några få undantag överförs energi på långa avstånd med hjälp av växelström eller trefas växelström.

För ca 100 år sedan var det vanligt med likströmsöverföring. Överföring av högspänd likström görs fortfarande på kablar som är långa och ligger på havsbotten (exempelvis kablar till Gotland och till Polen). Ända in på 1950-talet fanns det områden i Stockholm som endast försågs med likström.

Nackdelen med likströmsnät är att hela nätet måste ha samma spänning. Det går att komma runt problemet genom att låta likströmmen få driva en motor som i sin tur driver en generator som genererar en annan likspänning. På användarsidan om kabeln kan man ha en så kallad växelriktare som omvandlar likström till växelström. Arrangemanget är dyrt, skrymmande och har relativt sett låg verkningsgrad jämfört med "rent" växelströmssystem där det går att transformera växelströmmen till en praktiskt taget godtycklig spänning utan några större förluster.

Överföring av växelström över långa avstånd fordrar en teknik som minimerar de elektriska förlusterna.

Värmen som utvecklas i ledningarna är lika med strömmen i kvadrat gånger ledningarnas resistans. Höjer man spänningen på det elektriska nätet så minskar strömmen i motsvarande grad för en given överföringseffekt. Är ledningarna grova blir resistansen låg och därmed även förlusterna låga. Med grova ledningar blir det också möjligt att överföra stora effekter. För överföring på långa sträckor används 400 kV spänning.

För att få det 400/230 V system vi har på "förbrukarnivå", d.v.s. i hemmen, på företag och för andra "slutanvändare" behöver den höga spänningen transformeras till en lägre spänning. Förr hade vi 380/220 V trefas medan man nu har den internationellt överenskomna spänningen 400/230 V. Nedtransformeringen av spänningen sker vanligtvis i många steg på vägen till "förbrukaren" (kunden).

Jordade elsystem

När man har höga spänningar behövs ett så kallat jordat elsystem.

Idén är att man på elektriska apparater med elektriskt ledande höljen lägger potentialen (spänningen) på höjet på samma nivå som exempelvis värmeelement, vattenkranar, diskbänkar m.m. Idén är att ha punkter eller föremål som har samma potential. Kommer dessa föremål i kontakt med varandra så får vi ingen ström att gå mellan föremålen. Vi har med andra ord fått ett säkert elektriskt system.

Trefas växelström'

Skulle man välja att överföra ström med exempelvis tre separata jordade system så behövs sammanlagt nio (eller minst 6) ledare. Fördelen med ett sådant system kan vara att det inte fordras någon "synkronisering" eller något inbördes förhållande mellan växelspänningarna.

Ett effektivare överföringssystem är det vi kallar trefas växelström.

De tre faserna kan ha en gemensam ledare (återledare) om faserna är synkroniserade (d.v.s. står i ett fixt förhållande till varandra). Vid så kallad symetrisk belastning, lika belastning för faserna, kommer strömmen i återledaren att bli noll.

Med ett trefassystem kan man överföra samma effekt och lika säkert med fem ledare i stället för nio (eller 6) med ett system med tre "osynkroniserade" spänningar.

Fördelen med systemet är också att trefasmotorer blir mycket enkla till sin konstruktion, motorer får lång livslängd eftersom inga förslitningsdelar behöver ingå (förutom lager till axeln) och dessa apparater får hög verkningsgrad. För trefasmotorer är livslängden endast beroende av lagrens hållbarhet och att motorn inte överbelastas så mycket att den ökande värmeutvecklingen i motorn förstör ledningarnas isolering.

I ett 400/230 V system har man 230 V mellan fas och "nollan" (den gemensamma återledaren) och 400 V mellan faserna. Dessa spänningar är effektivvärden.

230 V är den spänning man vanligtvis har i väggkontakter, medan mer effektkrävande utrustning kopplas till till trefas 400/230 V system.

Faserna i ett trefassystem kallas L1,L2 och L3 eller L1,L2 och L\displaystyle _3. Till detta kommer återledaren, N, som det idealt sett aldrig går någon ström i.

Dessa faser ligger 120° fasförskjutna i förhållande till varandra.

Induktans och kapacitans

Induktans är en egenskap hos elektriska komponenter som innebär att elektrisk energi lagras upp i komponenten i form av ett magnetfält. Induktans har med tiden blivit en alltmer använd benämning på den typ av komponent som tidigare kallades induktor. I dagligt tal brukar dessa komponenter kallas spolar.

Induktans mäts i enheten Henry (H). Då 1 H är en mycket stor induktans använder man sig oftast av milliHenry, mH.

Enkelt uttryckt kan man säga att en induktans strävar efter att förhindra att strömmen genom den ändras. Det innebär att höga frekvenser dämpas mera än låga frekvenser. Induktanser används därför ofta i elektriska filter.

Stora induktanser är tunga och utrymmeskrävande på grund av att de lindas runt järnkärnor. Det är också svårt att producera induktanser med god noggrannhet. Därför har man i modern elektronik ofta ersatt induktanserna med kapacitivt återkopplade operationsförstärkare, vilka ger kretsen ungefär samma egenskaper.

Exempel på andra elektriska komponenter som har stor induktans är motorer och transformatorer (som ju båda innehåller spolar runt järnkärnor).

Kapacitans är förmågan att lagra elektrisk laddning, den utmärkande egenskapen för en elektrisk kondensator. Ordet kapacitans används även ibland istället för ordet kondensator. Kapacitans mäts i enheten farad som är en coulomb (amperesekund) per volt.

Växelspänningseffekt och impedans

Frekvens

Frekvensen \displaystyle f beskriver hur många gånger per tidsenhet som en ström växlar polaritet, normalt mäter vi i enheten \displaystyle 1 Hz = 1 s^{-1}.

Vid energiöverföring har man fasta frekvenser där alla elverk som är hopkopplade jobbar synkront med exakt samma frekvens. Det finns en internationell standard som förespråkar \displaystyle f = 50 Hz. Det är vad vi har i Europa. I vissa fall som t.ex. för svensk järnvägstrafik, väljer man att omforma den till 1632 Hz.

I Amerika har man valt en annan frekvens, \displaystyle f = 60 Hz, för energiöverföring. Där är också i de allra flesta fallen systemspänningen vid enfas 110-120 V. Trefas är inget man kopplar in till hushållen där.

Slutligen används olika frekvenser för informationsöverföring, man pratar bland annat om bärvåg som är den frekvensen som informationen är in närheten av. Exempel på bärvågar är 92,40 MHz (P1), 900 MHz för mobiltelefoni, 100 MHz för datakommunikation mm.

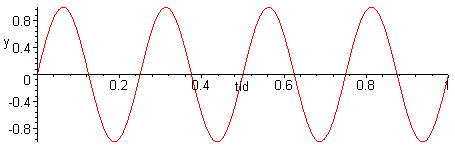
I grafen ovan syns en växelspänning med frekvensen 4 Hz. På 1 sekund hinner vi med fyra hela svängningar. Så låga frekvenser används i princip aldrig.

Vinkelfrekvens \displaystyle \omega

Inom elläran har det visat sig praktiskt att istället räkna med hur många radianer per sekund strömmen ändrar sig. Eftersom det på ett varv går \displaystyle 2\pi radianer får vi sambandet mellan antalet radianer per sekund \displaystyle \omega och frekvens \displaystyle f som

\displaystyle \omega = 2\pi \cdot f

Impedans

Ohms lag gäller egentligen för det totala motståndet, \displaystyle Z. Vi kallar det impedans. I likspänningsfallet är \displaystyle Z alltid lika med \displaystyle R, så är det inte när vi har växelspänning!

Ohms lag lyder alltså från och med nu \displaystyle U = Z\cdot I

Resistans Motstånd har en resistans \displaystyle R\Omega, resistansen beskriver hur mycket ström som kan strömma genom motståndet.

På motsvarande sätt har även spolar och kondensatorer motstånd fast dessa beror på vilken frekvens strömmen genom dem har.

För en spole betecknar vi detta motsånd med \displaystyle X_L, och den beror av frekvensen enligt följande.

\displaystyle X_L = \omega L, enhet \displaystyle 1\Omega

För en kondensator finner vi på samma sätt för \displaystyle X_C sambandet

\displaystyle X_C = \frac{1}{\omega C}, enhet \displaystyle 1\Omega

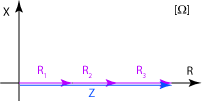
Impedans hos seriekopplade komponenter - Visardiagram

En modell för att räkna ut den sammansatta impedansen är att använda visardiagram i Z-planet med en R- och en X-axel. Impedanskomponenterna ovan har då följande riktningar

\displaystyle R - riktat positivt i R-led
\displaystyle X_L - riktat positivt i X-led
\displaystyle X_C - riktat negativt i X-led

Exempel 1

Vi tittar på tre resistorer och söker den sammanlagda impedansen.

Vi ritar in komponenternas impedanser i visardigrammet som ett polygontåg. Resultanten Z är den totala impedansen som i detta fall även är en resistans eftersom den inte har någon vinkel mot R-axeln.

Vi finner att \displaystyle R = R_1 + R_2 + R_3, i detta fall var det onödigt att använda visardiagrammet! Impedansen visade sig vara rent resistiv.

Exempel 2

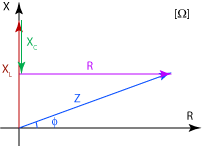
Vi tittar på en spole, en resistor och en kondensator och söker den sammanlagda impedansen.

Vi ritar in komponenternas impedanser i vårt visardiagram nedan, denna gång går inte alla åt samma håll.

Vi inser att vi med hjälp av Pythagoras sats enkelt får summan som

\displaystyle Z = \sqrt{((X_L - X_C)^2 + R^2}

Enheten är \displaystyle 1 \Omega.

Fasvinkel \displaystyle \phi

Från andra exemplet ovan inser vi att \displaystyle Z inte alltid är riktat i R-riktningen. Vi brukar kalla vinkeln mellan \displaystyle Z och R-axeln för fasvinkel. Fasvinkeln betecknas ofta med \displaystyle \phi.

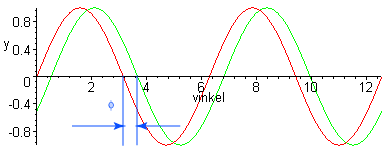
I en växelströmskrets kan det vara så att ström och spänning ligger i ofas, strömmens toppar kommer fram innan spänningens toppar eller tvärt om. I bilden nedan är det egentligen ström respektive spänning på y-axeln. X-axeln är graderad i radianer.