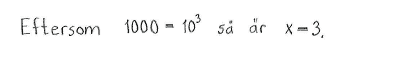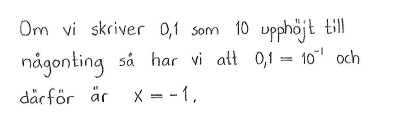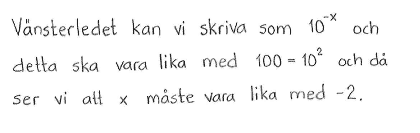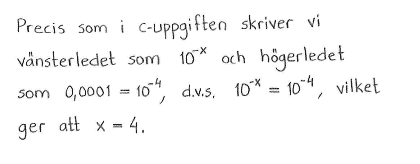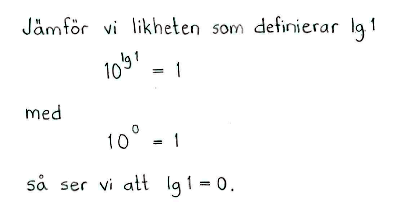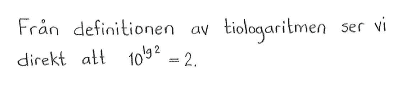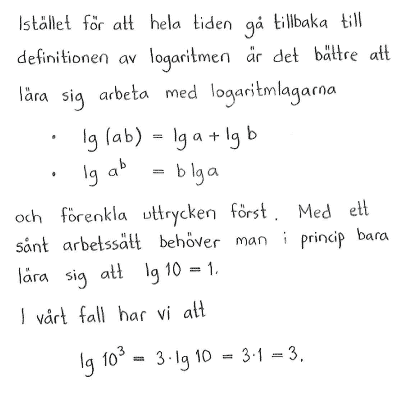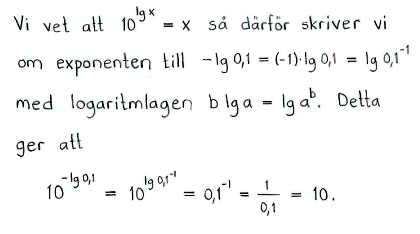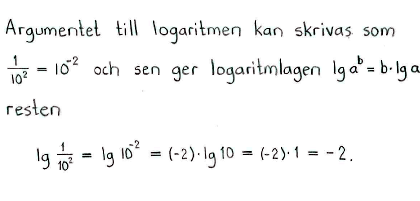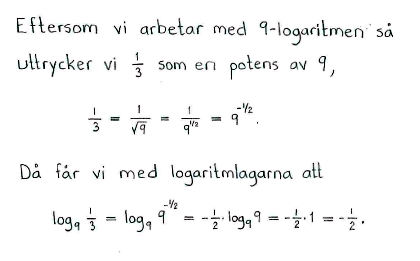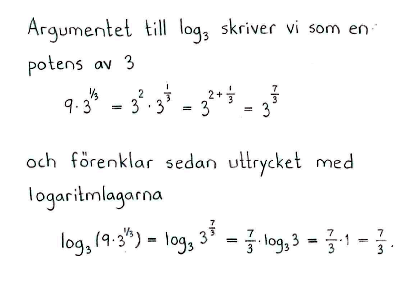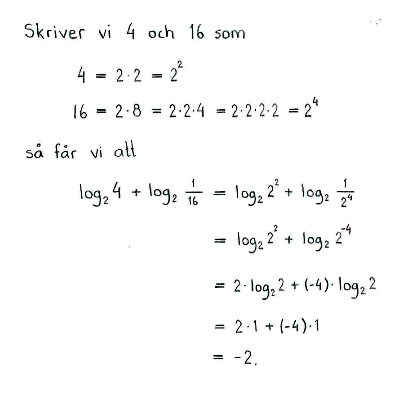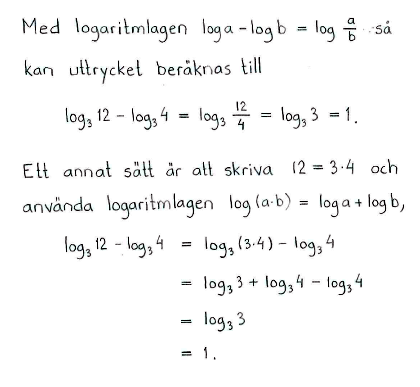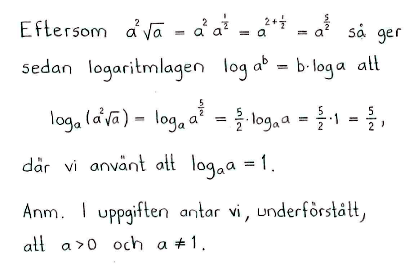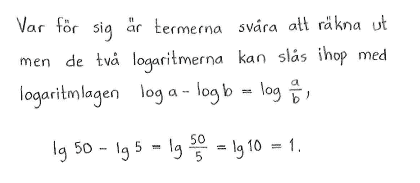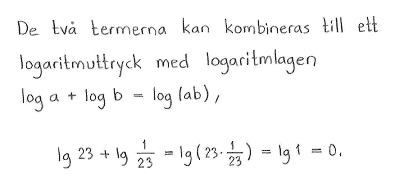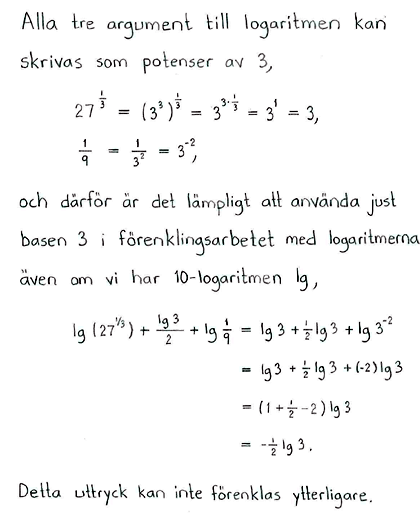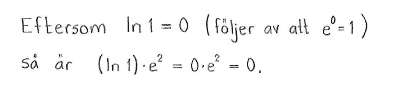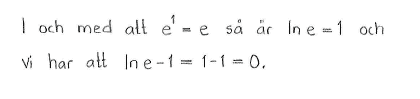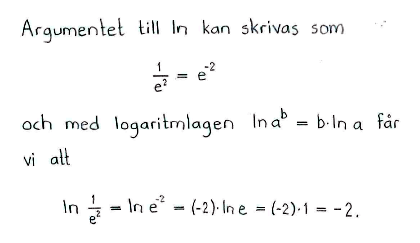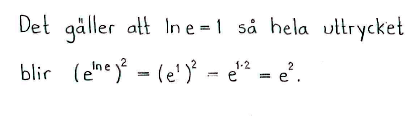3.3 Övningar
Sommarmatte 1
Innehåll |
[redigera] Övning 3.3:1
Bestäm $\,x\,$ om
| a) | $10^x=1\,000$ | b) | $10^x=0{,}1$ |
| c) | $\displaystyle \frac{1}{10^x}=100$ | d) | $\displaystyle \frac{1}{10^x}=0{,}000\,1$ |
Facit till alla delfrågor
| a) | $x=3$ | b) | $x=-1$ |
| c) | $x=-2$ | d) | $x=4$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
[redigera] Övning 3.3:2
Beräkna
| a) | $\lg{ 0{,}1}$ | b) | $\lg{ 10\,000}$ | c) | $\lg {0{,}001}$ | d) | $\lg {1}$ |
| e) | $10^{\lg{2}}$ | f) | $\lg{10^3}$ | g) | $10^{-\lg{0{,}1}}$ | h) | $\lg{\displaystyle \frac{1}{10^2}}$ |
Facit till alla delfrågor
| a) | $-1$ | b) | $4$ | c) | $-3$ | d) | $0$ |
| e) | $2$ | f) | $3$ | g) | $10$ | h) | $-2$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
Lösning till delfråga g)
|
|
Lösning till delfråga h)
|
|
[redigera] Övning 3.3:3
Beräkna
| a) | $\log_2{8}$ | b) | $\log_9{\displaystyle \frac{1}{3}}$ | c) | $\log_2{0{,}125}$ |
| d) | $\log_3{\left(9\cdot3^{1/3}\right)}$ | e) | $2^{\log_{\scriptstyle2}{4}}$ | f) | $\log_2{4}+\log_2{\displaystyle \frac{1}{16}}$ |
| g) | $\log_3{12}-\log_3{4}$ | h) | $\log_a{\bigl(a^2\sqrt{a}\,\bigr)}$ | ||
Facit till alla delfrågor
| a) | $3$ | b) | $-\displaystyle \frac{1}{2}$ | c) | $-3$ |
| d) | $\displaystyle \frac{7}{3}$ | e) | $4$ | f) | $-2$ |
| g) | $1$ | h) | $\displaystyle \frac{5}{2}$ | ||
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
Lösning till delfråga g)
|
|
Lösning till delfråga h)
|
|
[redigera] Övning 3.3:4
Förenkla
| a) | $\lg{50}-\lg{5}$ | b) | $\lg{23}+\lg{\displaystyle \frac{1}{23}}$ | c) | $\lg{27^{1/3}}+\displaystyle \frac{\lg{3}}{2}+\lg{\displaystyle \frac{1}{9}}$ |
Facit till alla delfrågor
| a) | $1$ | b) | $0$ | c) | $-\displaystyle \frac{1}{2}\lg{3}$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
[redigera] Övning 3.3:5
Förenkla
| a) | $\ln{e^3}+\ln{e^2}$ | b) | $\ln{8}-\ln{4}-\ln{2}$ | c) | $(\ln{1})\cdot e^2$ |
| d) | $\ln{e}-1$ | e) | $\ln{\displaystyle \frac{1}{e^2}}$ | f) | $\left(e^{\ln{e}}\right)^2$ |
Facit till alla delfrågor
| a) | $5$ | b) | $0$ | c) | $0$ |
| d) | $0$ | e) | $-2$ | f) | $e^2$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
[redigera] Övning 3.3:6
Använd miniräknaren till höger för att beräkna med tre decimaler (Knappen LN betecknar den naturliga logaritmen i basen e):
| a) | $\log_3{4}$ |
| b) | $\lg{46}$ |
| c) | $\log_3{\log_2{(3^{118})}}$ |
Facit till alla delfrågor
| a) | $1{,}262$ |
| b) | $1{,}663$ |
| c) | $4{,}762$ |
Lösning till delfråga a)
|
|
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
|
|
