2.2 Linjära uttryck
Sommarmatte 1
| Versionen från 16 maj 2007 kl. 07.29 (redigera) Tek (Diskussion | bidrag) (Lagt in text om grund- och slutprov) ← Gå till föregående ändring |
Versionen från 21 maj 2007 kl. 13.45 (redigera) (ogör) Lina (Diskussion | bidrag) m (→Förstagradsekvationer) Gå till nästa ändring → |
||
| Rad 48: | Rad 48: | ||
| :$x+3-3=7-3$. <br> | :$x+3-3=7-3$. <br> | ||
| Vänsterledet förenklas då till $x$ och vi får att <br> | Vänsterledet förenklas då till $x$ och vi får att <br> | ||
| - | :$x=7-3=4.$ <br><br> | + | :$x=7-3=4$. <br><br> |
| <li>Lös ekvationen $3x=6$. <br><br> | <li>Lös ekvationen $3x=6$. <br><br> | ||
| Dividera båda led med $3$ <br> | Dividera båda led med $3$ <br> | ||
| Rad 139: | Rad 139: | ||
| </div> | </div> | ||
| - | |||
| ==Räta linjer== | ==Räta linjer== | ||
Versionen från 21 maj 2007 kl. 13.45
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|
TeoriFörstagradsekvationerFör att lösa förstagradsekvationer (även kallade linjära ekvationer) utför vi räkneoperationer på båda leden samtidigt, som successivt förenklar ekvationen och till slut gör att vi får $x$ ensamt i ena ledet. Exempel 1
En förstagradsekvation kan skrivas på normalformen $\,ax=b$. Lösningen är då helt enkelt $x=b/a$ (man måste anta att $a\not=0$). De eventuella svårigheter som kan uppstå när man läser en förstagradsekvation gäller alltså inte själva lösningsformeln utan snarare de förenklingar som kan behövas för att komma till normalformen. Här nedan visas några exempel som har det gemensamt att en ekvation förenklas till linjär normalform och därmed får en unik lösning.
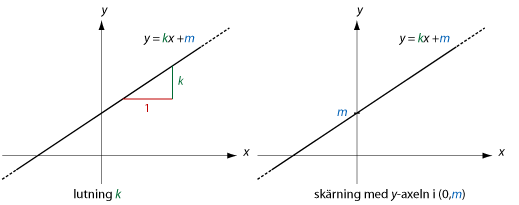
Exempel 2 Lös ekvationen $\,2x-3=5x+7$. Exempel 3 Lös ut $x$ från ekvationen $ax+7=3x-b$. Det är inte alltid uppenbart att man har att göra med en förstagradsekvation. I följande två exempel förvandlas den ursprungliga ekvationen genom förenklingar till en förstagradsekvation. Exempel 4 Lös ekvationen $\ (x-3)^2+3x^2=(2x+7)^2$. Exempel 5 Lös ekvationen $\displaystyle\ \frac{x+2}{x^2+x}=\displaystyle \frac{3}{2+3x}$. Flytta över båda termerna i ena ledet $$\displaystyle \frac{x+2}{x^2+x}-\frac{3}{2+3x}= 0\; \mbox{.}$$ Förläng termerna så att de får samma nämnare $$\displaystyle \frac{(x+2)(2+3x)}{(x^2+x)(2+3x)}-\frac{3(x^2+x)}{(2+3x)(x^2+x)}= 0$$ och förenkla täljaren $$\displaystyle \frac{(x+2)(2+3x)-3(x^2+x)}{(x^2+x)(2+3x)} = 0,$$ $$\displaystyle \frac{3x^2+8x+4-(3x^2+3x)}{(x^2+x)(2+3x)} = 0,$$ $$\displaystyle \frac{5x +4}{(x^2+x)(2+3x)} = 0.$$ Denna ekvation är uppfylld bara när täljaren är lika med noll (samtidigt som nämnaren inte är lika med noll), $$5x+4=0$$ vilket ger att $\,x=-\displaystyle \frac{5}{4}$. Räta linjerFunktioner av typen $$y=2x+1$$ $$y=-x+3$$ $$y=\displaystyle \frac{1}{2} x -5 $$ är exempel på linjära funktioner och de kan allmänt skrivas i formen $$y=kx+m$$ där $k$ och $m$ är konstanter. Grafen till en linjär funktion är alltid en rät linje och konstanten $k$ anger linjens lutning mot $x$-axeln och $m$ anger $y$-koordinaten för den punkt där linjen skär $y$-axeln. Konstanten $k$ kallas för linjens riktningskoefficient och innebär att en enhetsförändring i positiv $x$-led på linjen ger $k$ enheters förändring i positiv $y$-led. Det gäller därmed att om
För en horisontell linje (parallell med $x$-axeln) är $\,k=0\,$ medan en vertikal linje (parallell med $y$-axeln) inte har något $k$-värde (en sådan linje kan inte skrivas i formen $y=kx+m$).
Exempel 6
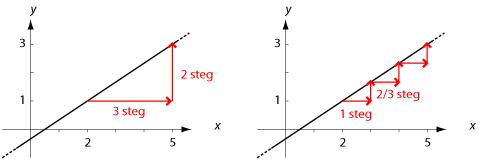
Exempel 7 Vilken riktningskoefficient har den räta linje som går genom punkterna $(2,1)$ och $(5,3)$?
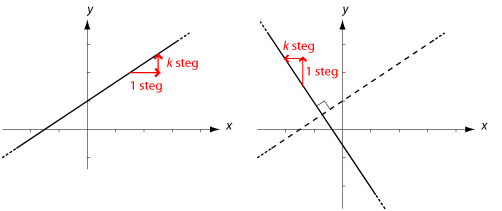
Två räta linjer som är parallella har uppenbarligen samma riktningskoefficient. Det går också att se (t.ex i figuren nedan) att två linjer som är vinkelräta har riktningskoefficienter $k_1$ respektive $k_2$ som uppfyller $k_2 = -\frac{1}{k_1}$ , vilket också kan skrivas som $k_1 k_2 = -1$. Bildtext: Den räta linjen i figuren till vänster har riktningskoefficient $k$, d.v.s. $1$ steg i $x$-led motsvaras av $k$ steg i $y$-led. Om linjen vrids $90^\circ$ motsols får vi linjen i figuren till höger, och den linjen har riktningskoefficient $-\frac{1}{k}$ eftersom nu motsvaras $-k$ steg i $x$-led av $1$ steg i $y$-led. Exempel 8
Alla räta linjer (även den vertikala linjen) kan skrivas i den allmänna formen $$ax+by=c$$ där $a$, $b$ och $c$ är konstanter.
Exempel 9
Här kan du se hur linjens ekvation kan skrivas utifrån att man vet koordinaterna för två punkter på linjen. Här kan du ändra på k och m och se hur detta påverkar linjens egenskaper.
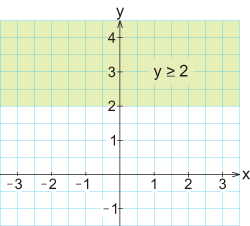
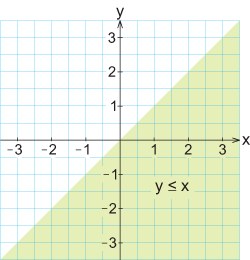
Områden i koordinatsystemGenom att tolka olikheter geometriskt kan de användas för att beskriva områden i planet. Exempel 10
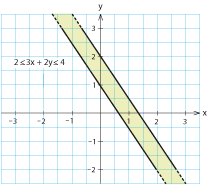
Exempel 11 Skissera området i $x,y$-planet som uppfyller $2 \le 3x+2y\le 4$.
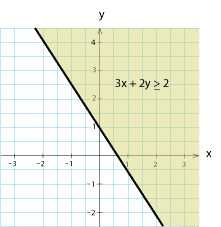
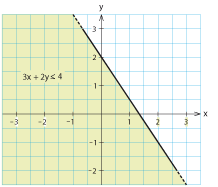
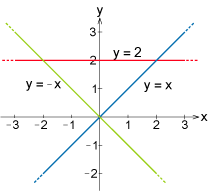
$$3x+2y \ge 2 \quad \mbox{och} \quad 3x+2y\le4 \;\mbox{.}$$ Flyttar vi över $x$-termerna till högerledet och delar båda led med $2$ får vi $$y \ge 1-\frac{3}{2}x \quad \mbox{och} \quad y\le 2-\frac{3}{2}x \;\mbox{.}$$ De punkter som uppfyller den första olikheten ligger på och ovanför linjen $\,y \ge 1-\frac{3}{2}x\,$ medan de punkter som uppfyller den andra olikheten ligger på eller under linjen $y\le 2-\frac{3}{2}x$. Punkter som uppfyller båda olikheterna tillhör det bandformade område som de gråa områdena ovan har gemensamt. Exempel 12 Om vi ritar upp linjerna $\,y=x$, $\,y=-x\,$ och $\,y=2\,$ så begränsar dessa linjer en triangel, i koordinatsystemet.
Vi ser att dess $y$-koordinat måste vara mindre än $2$. Samtidigt ser vi att triangeln nedåt begränas av $ y=0$. $y$-koordinaten måste således ligga i intervallet $ 0\le y\le2$. För $x$-koordinaten blir det lite mer komplicerat. Vi ser att $x$-koordinaten måste ligga ovanför linjerna $y=-x \mbox{ och } y=x$. Vi ser att detta är uppfyllt då $-y\le x\le y$. Eftersom vi redan har begränsningar för $y$-koordinaten så ser vi att $x$ inte kan vara större än $2$ och mindre än $-2$ automatiskt. Vi ser att basen i triangeln blir $4$ längdenheter och höjden $2$ längdenheter. Arean av denna triangel blir alltså $ 4\cdot 2/2=4$areaenheter. Råd för inläsning Grund- och slutprov Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge.
Rita egna figurer när du löser geometriska problem och att vara noggrann när du ritar! En bra figur kan vara halva lösningen, men en dålig figur kan lura en.
för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om: Läs mer om räta linjens ekvation i Bruno Kevius matematiska ordlista
|
|