4.1 Vinklar och cirklar
Sommarmatte 1
| Versionen från 24 april 2007 kl. 10.52 (redigera) Lina (Diskussion | bidrag) (→Cirklar) ← Gå till föregående ändring |
Versionen från 24 april 2007 kl. 10.53 (redigera) (ogör) Lina (Diskussion | bidrag) (→Cirklar) Gå till nästa ändring → |
||
| Rad 130: | Rad 130: | ||
| Bild:figur 3.2.8 | Bild:figur 3.2.8 | ||
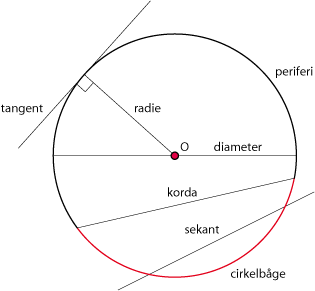
| - | Avståndet $r$ kallan för cirkelns radie och punkten $(a,b)$ för cirkelns medelpunkt. Figuren nedan visar andra cirkelbegrepp. | + | Avståndet $r$ kallan för cirkelns radie och punkten $(a,b)$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp. |
| [[Bild:3_2_10.gif]] | [[Bild:3_2_10.gif]] | ||
Versionen från 24 april 2007 kl. 10.53
4.1 Vinklar och cirklarInnehåll:
Läromål: Efter detta avsnitt ska du ha lärt dig att:
|
||
TeoriVinkelmåttDet finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer.
Bild: figur 3.2.1
Bild: figurer 3.2.2 och figurer 3.2.3
Exempel 1
I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än $360^\circ$. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv. Bild: Figur 3.2.4 Exempel 2 Exempeltext, använd nedanstående numrering
AvståndsformlenPythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $a$ och $b$ , och hypotenusa $c$ gäller att $$c^2 = a^2 + b^2 \; \mbox{.}$$ Bild: figur 3.2.5 Exempel 3 Bild: figur 3.2.6 I triangel till höger är $$c^2= 3^2 + 4^2 = 9 +16 = 25$$ och därför är hypotenusan $c$ lika med $$c=\sqrt{25} = 5 \; \mbox{.}$$
Avståndsformeln: Avståndet $d$ mellan två puntker med koordinater $(x, y)$ och $(a, b)$ är $$d = \sqrt{(x – a)^2 + (y – b)^2} $$ Denna formel kallas för avståndsformeln. Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna. Bild: figur 3.2.7 Kateternas längd är lika med beloppet av skillnaden i $x$- och $y$-led mellan punkterna, d.v.s. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln. Exempel 4
Interaktivt experiment: Här kan du experimentera med avståndsformeln och Pythagoras sats CirklarEn cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $r$ från en punkt $(a,b)$. Bild:figur 3.2.8 Avståndet $r$ kallan för cirkelns radie och punkten $(a,b)$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp. Exempel 5 En cirkelsektor är given i figuren till höger. Bild: figur 3.2.10
<img src="ppStdFiles2261/774115.gif" hspace='0' vspace='0' /> Cirkelsektorer och båglängder<img src="object49972/bilder/3_2/3_2_04.gif" align="right">Om vi har öppningsvinkeln $\alpha$ för en cirkelsektor kan vi beräkna cirkelsektorns area A och cirkelbågens båglängd b, genom att betrakta dem som en andel av en hel cirkel. Eftersom en hel cirkel har omkretsen $2\pi r$ och arean $\pi r^2$, får vi bågens längd utefter cirkelsektorn $= b = \displaystyle\frac{\alpha}{2\pi} 2\pi r = \alpha r$ arean $= A = \displaystyle\frac{\alpha}{2\pi} \pi r^2 = \displaystyle\frac{\alpha r^2}{2}$ Observera att vinkeln $\alpha$ måste anges i radianer för att formlerna skall bli så snygga.
Definition av en cirkel<img src="object49972/bilder/3_2/3_2_08.gif" align="right"> En cirkel kan definieras som mängden av alla punkter (x, y) som ligger på ett visst avstånd r från en given punkt (a, b). Avståndet r blir då cirkels radie, och punkten (a, b) blir cirkelns medelpunkt. Detta ger med hjälp av avståndsformeln villkoret
$r = \sqrt{(x – a)^2 + (y – b)^2}$.
Detta villkor brukar genom kvadrering skrivas
$(x – a)^2 + (y – b)^2 = r^2$
och kallas för cirkelns ekvation. Cirkeln är alltså mängden av alla punkter $(x, y)$ som uppfyller ekvationen $(x – a)^2 + (y – b)^2 = r^2$ och ligger på avståndet r från punkten $(a, b)$. Om man sätter r = 1 och $(a,b) = (0,0)$ får man en cirkel med radien 1 och medelpunkten i origo. Denna cirkel kallas enhetscirkeln. Enhetscirkeln är ett viktigt hjälpmedel i många sammanhang, t.ex. när man arbetar med trigonometriska funktioner.
Några fakta om cirklar
Några viktiga begrepp
Det är inte alltid helt enkelt att känna igen ekvationen för en cirkel. Med hjälp av kvadratkomplettering (tidigare presenterat i avsnitt 2.3) kan man skriva ekvationen på så kallad standardform, där går det direkt att avläsa cirkelns radie och medelpunkt.
Exempel 1 Skissera cirkeln $ x^2 + y^2 = 4$ Lösning: Vi jämför den aktuella cirkeln med cirkelns ekvation.
$(x-x_0)^2+(y-y_0)^2=r^2$
Vi ser att i vårt fall är
$x_0=0$ och $y_0=0$
Detta betyder alltså att cirkeln har sin medelpunkt i $(0,0)$ dvs i origo.
Radien på cirkeln går att avläsa ur högerledet:
$r = \sqrt {r^2} = \sqrt 4 = 2$
Med denna information kan vi skissera cirkeln enligt nedan.<p align="center"><img src="ppStdFiles2261/766791.gif" hspace='0' vspace='0' />
Exempel 2 Bestäm medelpunkten för den cirkel vars ekvation är $x^2 + y^2 – 2x + 4y + 1 = 0$.
Lösning: Vi försöker skriva om på normalformen av cirkelns ekvation, $(x-x_0)^2+(y-y_0)^2=r^2$, där $(x_0,y_0)$ är centrum och $r$ är radien.
Vi utgår från de termer som innehåller $x\;$, nämligen $\; x^2-2x$
och skriver om den m.h.a. andra kvadreringsregeln,
$ a^2-2ab+b^2=(a-b)^2 $
Vi identifierar $ a=x $ och $ b=1 $ vilket ger $ b^2=1 $, vi har då
$ x^2-2x=(x-1)^2-1 $
På samma sätt får vi för termerna $ y^2 + 4y $
$ y^2+4y=(y+2)^2-4 $
Vår ursprungliga ekvation $ x^2+y^2-2x+4y+1=0 $ kan då skrivas som
$ (x-1)^2-1+(y+2)^2-4+1=0 $
vilket förenklas till
$ (x-1)^2 + (y+2)^2 = 4 $
Vi jämför med cirkelns ekvation på normalform och identifierar medelpunkten $ (x_0,y_0)=(1,-2) $ samt radien $ \sqrt{4}=2 $ .
Denna information behövs om du vill rita figuren, utgå då från medelpunkt och radie enligt ovan.<p align="center"><img src="ppStdFiles2261/766790.gif" hspace='0' vspace='0' />
Råd för inläsning Tänk på att: Lär dig att använda enhetscirkeln som ett verktyg i det trigonometriska arbetet. Avläsningar i enhetscirkeln ger dig viktiga upplysningar om diverse samband.
för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om: Sammanfattning av Geometri B ur Theducations gymnasielexikon Läs mer om Pythagoras sats på svenska Wikipedia Läs mer i Mathworld om cirkeln
Experimentera med Randvinkelsatsen
|
|