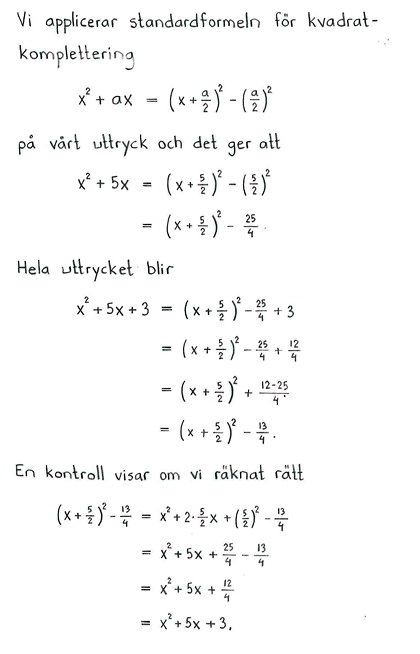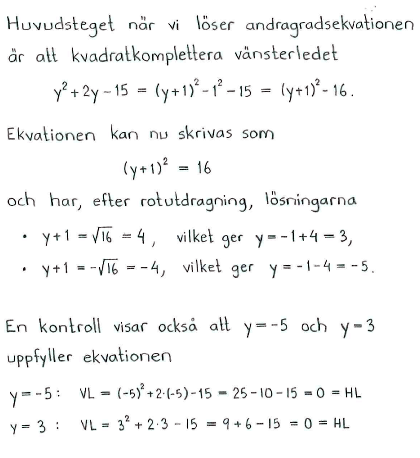2.3 Övningar
Sommarmatte 1
(Skillnad mellan versioner)
| Versionen från 28 april 2007 kl. 18.39 (redigera) Ossiang (Diskussion | bidrag) (→Övning 2.3:2) ← Gå till föregående ändring |
Versionen från 28 april 2007 kl. 18.40 (redigera) (ogör) Ossiang (Diskussion | bidrag) (→Övning 2.3:2) Gå till nästa ändring → |
||
| Rad 161: | Rad 161: | ||
| </div> | </div> | ||
| </div> | </div> | ||
| + | |||
| + | ==Övning 2.3:3== | ||
Versionen från 28 april 2007 kl. 18.40
Övning 2.3:1
Kvadratkomplettera följande uttryck
| a) | $x^2-2x$ | b) | $x^2+2x-1$ | c) | $5+2x-x^2$ | d) | $x^2+5x+3$ |
Facit
Facit till alla delfrågorna
| a) | $(x-1)^2-1$ | b) | $(x+1)^2-2$ | c) | $-(x-1)^2+6$ | d) | $\left(x+\displaystyle \frac{5}{2}\right)^2-\displaystyle \frac{13}{4}$ |
Övning 2.3:2
Lös följande andragradsekvationer med kvadratkomplettering
| a) | $x^2-4x+3=0$ | b) | $y^2+2y-15=0$ | c) | $y^2+3y+4=0$ |
| d) | $4x^2-28x+13=0$ | e) | $5x^2+2x-3=0$ | f) | $3x^2-10x+8=0$ |
Facit
Facit till alla delfrågorna
| a) | $\left\{ \matrix{ x_1 = 1 \cr x_2 = 3 }\right. $ | b) | $ \left\{ \matrix{ y_1 = -5 \cr y_2 = 3 }\right. $ | c) | saknar lösning* |
| d) | $ \left\{ \matrix{ x_1 = \frac{1}{2} \cr x_2 = \frac{13}{2} }\right. $ | e) | $\left\{ \matrix{ x_1 = -1 \cr x_2 = \frac{3}{5} }\right. $ | f) | $ \left\{ \matrix{ x_1 = \frac{4}{3} \cr x_2 = 2 }\right. $ |
- ) ekvationen saknar reella lösningar