2. Algebra
Sommarmatte 1
| Versionen från 10 maj 2007 kl. 15.44 (redigera) Lina (Diskussion | bidrag) ← Gå till föregående ändring |
Nuvarande version (12 januari 2008 kl. 11.05) (redigera) (ogör) KTH.SE:u1m1gion (Diskussion | bidrag) m |
||
| (5 mellanliggande versioner visas inte.) | |||
| Rad 19: | Rad 19: | ||
| + | Algebra är den gren av matematiken som behandlar räkning med symboliska uttryck och variabler och inte bara räkning med tal. | ||
| + | Algebra behövs i många situationer, t.ex. kan algebra användas till att beskriva matematiska problem och till att lösa ekvationer. Det går bland annat att beskriva geometriska fakta med hjälp av algebraiska påståenden, och många problem går att lösa med hjälp av algebraiska operationer. | ||
| - | Algebra är den gren av matematiken som behandlar räkning med symboliska uttryck och variabler och inte bara räkning med tal. | ||
| - | |||
| - | Algebra behövs i många situationer, t.ex. kan algebra användas till att beskriva matematiska problem och till att lösa ekvationer. Det går bland annat att beskriva geometriska fakta med hjälp av algebraiska påståenden, och många problem går att lösa med hjälp av algebraiska operationer. | ||
| - | I en del fall kan man inte räkna ut värdet av ett uttryck till ett numeriskt värde. Anledningen kan vara att uttrycket innehåller obekanta parametrar eller variabler. | + | I en del fall kan man inte räkna ut värdet av ett uttryck till ett numeriskt värde. Anledningen kan vara att uttrycket innehåller obekanta parametrar eller variabler. Det kan också vara så att det är viktigt att ett tal är exakt, t.ex. att en viss cirkel har en omkrets som är exakt $4\pi$, eller hypotenusans längd för en triangel är $\sqrt{3}$, eller varför inte att värdet på en konstant är $\displaystyle\frac{1-\ln 2}{3}$. |
| - | Det kan också vara så att det är viktigt att ett tal är exakt, t.ex. att en viss cirkel har en omkrets som är exakt $4\pi$, eller hypotenusans längd för en triangel är $\sqrt{3}$, eller varför inte att värdet på en konstant är $\displaystyle\frac{1-\ln 2}{3}$. | ||
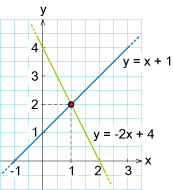
| + | [[Bild:772682.gif|thumb|250px|En linjär ekvation med två obekanta kan ses som en linje i ett koordinatsystem. Den gemensamma lösningen ( x, y ) till dessa ekvationer motsvaras då av den gemensamma punkten för dessa linjer, dvs. skärningspunkten.]] | ||
| Då kan det vara enklast att i uträkningarna kalla talet för exempelvis $a$. Som svar kan man också acceptera att man inte kommer fram till ett numeriskt värde, utan istället får ett uttryck som innehåller $a$. | Då kan det vara enklast att i uträkningarna kalla talet för exempelvis $a$. Som svar kan man också acceptera att man inte kommer fram till ett numeriskt värde, utan istället får ett uttryck som innehåller $a$. | ||
| En vanlig situation där man kan behöva algebra är förenkling. Det är ofta mycket viktigt att förenkla ett uttryck, t.ex. innan man skall derivera, eller när man löser en ekvation. | En vanlig situation där man kan behöva algebra är förenkling. Det är ofta mycket viktigt att förenkla ett uttryck, t.ex. innan man skall derivera, eller när man löser en ekvation. | ||
| + | |||
| Genom att förenkla minskar man risken för slarvfel och man slipper onödigt arbete. Att förenkla innebär att skriva om ett uttryck från en form till en annan. Vilken form som betraktas som ”enkel” är ibland uppenbart, men det kan också bero på vad man vill göra med uttrycket. | Genom att förenkla minskar man risken för slarvfel och man slipper onödigt arbete. Att förenkla innebär att skriva om ett uttryck från en form till en annan. Vilken form som betraktas som ”enkel” är ibland uppenbart, men det kan också bero på vad man vill göra med uttrycket. | ||
| + | |||
| När man deriverar kan det vara fördelaktigt att formulera uttrycket som en summa av ett antal termer. När man löser en ekvation kan det vara fördelaktigt att formulera det som en produkt av ett antal faktorer. Därför behöver man kunna omvandla uttryck mellan olika former. | När man deriverar kan det vara fördelaktigt att formulera uttrycket som en summa av ett antal termer. När man löser en ekvation kan det vara fördelaktigt att formulera det som en produkt av ett antal faktorer. Därför behöver man kunna omvandla uttryck mellan olika former. | ||
| - | '''Observera att materialet i denna kursdel---liksom i övriga delar av kursen---är utformat för att man ska arbeta med det utan hjälp av miniräknare.''' | + | '''Observera att materialet i denna kursdel – liksom i övriga delar av kursen – är utformat för att man ska arbeta med det utan hjälp av miniräknare.''' |
| - | ’’När du kommer till högskolan kommer du nämligen inte’’att få använda miniräknare på dina "tentor", åtminstone inte på grundkurserna. | + | ''När du kommer till högskolan kommer du nämligen inte att få använda miniräknare på dina "tentor", åtminstone inte på grundkurserna.'' |
| Rad 57: | Rad 58: | ||
| </div> | </div> | ||
| - | |||
| - | |||
| - | <div class="teori"> | ||
| - | |||
| - | © Copyright 2007, math.se | ||
| - | |||
| - | Materialet ovan ingår i kursen '''Förberedande kurs i matematik 1''' som ges som preparandutbildning av ett flertal universitet och högskolor inom samarbetet [http://math.se math.se]. Kursen ger högskolepoäng och berättigar till csn-bidrag. Förutom detta material ingår mentorstöd, examination via nätet samt tillgång till diskussionsforum. Kursstart sker löpande. | ||
| - | |||
| - | Sök kursen '''Förberedande kurs i matematik 1''' via [http://math.se math.se] | ||
| - | |||
| - | </div> | ||
| - | |||
| - | |||
Nuvarande version
Varför räknar vi med bokstäver och vem kom på detta?
Då kan det vara enklast att i uträkningarna kalla talet för exempelvis $a$. Som svar kan man också acceptera att man inte kommer fram till ett numeriskt värde, utan istället får ett uttryck som innehåller $a$. En vanlig situation där man kan behöva algebra är förenkling. Det är ofta mycket viktigt att förenkla ett uttryck, t.ex. innan man skall derivera, eller när man löser en ekvation.
När du kommer till högskolan kommer du nämligen inte att få använda miniräknare på dina "tentor", åtminstone inte på grundkurserna.
Så här lyckas du med Algebran
PS. Tycker du att innehållet i ett avsnitt känns väldigt bekant, så kan du testa att gå direkt till grundprovet och slutprovet. Du måste få alla rätt på ett prov, men kan göra om proven flera gånger, om du inte lyckas på första försöket. Det är ditt senaste resultat som visas i statistiken.
|
|