4.1 Vinklar och cirklar
Sommarmatte 1
| Versionen från 14 maj 2007 kl. 08.34 (redigera) Lina (Diskussion | bidrag) (→Avståndsformeln) ← Gå till föregående ändring |
Nuvarande version (25 maj 2007 kl. 15.18) (redigera) (ogör) Mikael (Diskussion | bidrag) (→Vinkelmått) |
||
| (20 mellanliggande versioner visas inte.) | |||
| Rad 42: | Rad 42: | ||
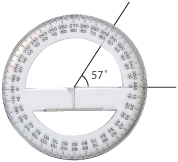
| *'''Grader.''' Om ett helt varv delas in i 360 delar, så kallas varje del 1 grad. Beteckningen för grader är $ ^\circ$. | *'''Grader.''' Om ett helt varv delas in i 360 delar, så kallas varje del 1 grad. Beteckningen för grader är $ ^\circ$. | ||
| - | [[Bild:3_2_1.gif]] | + | [[Bild:3_2_1.gif||center]] |
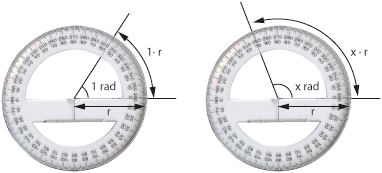
| *'''Radianer.''' Ett annat sätt att mäta vinklar är att använda längden av vinkelns cirkelbåge i förhållande till radien som mått på vinkeln. Detta vinkelmått kallas för radian. Ett varv är alltså $\,2\pi\,$ radianer eftersom cirkelns omkrets är $\,2\pi r\,$, där $\,r\,$ är cirkelns radie. | *'''Radianer.''' Ett annat sätt att mäta vinklar är att använda längden av vinkelns cirkelbåge i förhållande till radien som mått på vinkeln. Detta vinkelmått kallas för radian. Ett varv är alltså $\,2\pi\,$ radianer eftersom cirkelns omkrets är $\,2\pi r\,$, där $\,r\,$ är cirkelns radie. | ||
| - | [[Bild:3_2_2.gif]] | + | [[Bild:3_2_2.gif||center]] |
| Rad 65: | Rad 65: | ||
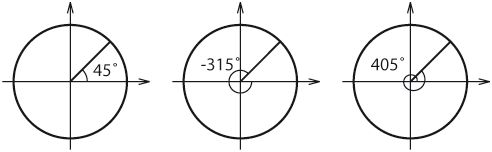
| I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än 360°. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv. | I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än 360°. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv. | ||
| - | [[Bild:3_2_4.gif]] | + | [[Bild:t_3_2_4.gif|center]] |
| <div class="exempel"> | <div class="exempel"> | ||
| Rad 84: | Rad 84: | ||
| ==Avståndsformeln== | ==Avståndsformeln== | ||
| - | [[Bild:3_2_5.gif|right]] | ||
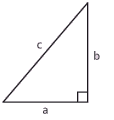
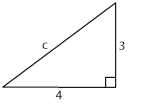
| Pythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $\,a\,$ och $\,b\,$, och hypotenusa $\,c\,$ gäller att | Pythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $\,a\,$ och $\,b\,$, och hypotenusa $\,c\,$ gäller att | ||
| - | |||
| <div class="regel"> | <div class="regel"> | ||
| + | [[Bild:T_3_2_5.gif|right]] | ||
| '''Pythagoras sats:''' | '''Pythagoras sats:''' | ||
| $$c^2 = a^2 + b^2\,\mbox{.}$$ | $$c^2 = a^2 + b^2\,\mbox{.}$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| </div> | </div> | ||
| Rad 116: | Rad 121: | ||
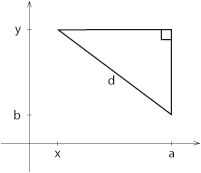
| Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna. | Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna. | ||
| - | [[Bild:3_2_7.gif]] | + | [[Bild:3_2_7.gif|center]] |
| Kateternas längd är lika med beloppet av skillnaden i ''x''- och ''y''-led mellan punkterna, dvs. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln. | Kateternas längd är lika med beloppet av skillnaden i ''x''- och ''y''-led mellan punkterna, dvs. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln. | ||
| Rad 136: | Rad 141: | ||
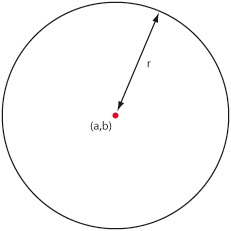
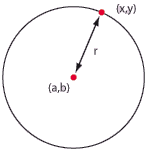
| En cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $\,r\,$ från en punkt $\,(a,b)\,$. | En cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $\,r\,$ från en punkt $\,(a,b)\,$. | ||
| - | Bild:figur 3.2.8 | + | [[Bild:3_2_8.gif|center]] |
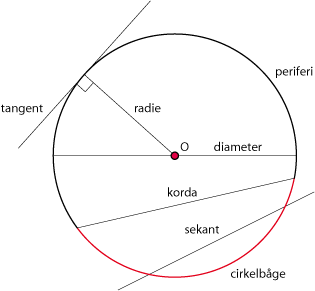
| Avståndet $\,r\,$ kallas för cirkelns radie och punkten $\,(a,b)\,$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp. | Avståndet $\,r\,$ kallas för cirkelns radie och punkten $\,(a,b)\,$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp. | ||
| - | [[Bild:3_2_10.gif||center]] | + | [[Bild:3_2_10.gif|center]] |
| Rad 146: | Rad 151: | ||
| '''Exempel 5''' | '''Exempel 5''' | ||
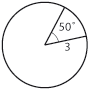
| - | En cirkelsektor är given i figuren till höger. Bild: figur 3.2.10 | + | En cirkelsektor är given i figuren till höger. [[Bild:t_3_2_9.gif|right]] |
| <ol type="a"> | <ol type="a"> | ||
| <li>Bestäm cirkelbågens längd. <br><br> | <li>Bestäm cirkelbågens längd. <br><br> | ||
| Rad 160: | Rad 165: | ||
| </div> | </div> | ||
| - | Bild:3.2.11 | + | |
| En punkt $\,(x,y)\,$ ligger på cirkeln som har medelpunkt i $\,(a,b)\,$ och radie $\,r\,$ om dess avstånd till medelpunkten är lika med $\,r\,$. Detta villkor kan formuleras med avståndsformeln som | En punkt $\,(x,y)\,$ ligger på cirkeln som har medelpunkt i $\,(a,b)\,$ och radie $\,r\,$ om dess avstånd till medelpunkten är lika med $\,r\,$. Detta villkor kan formuleras med avståndsformeln som | ||
| <div class="regel"> | <div class="regel"> | ||
| + | [[Bild:T_3_2_11.gif|right]] | ||
| '''Cirkelns ekvation:''' | '''Cirkelns ekvation:''' | ||
| $$(x – a)^2 + (y – b)^2 = r^2\,\mbox{.}$$ | $$(x – a)^2 + (y – b)^2 = r^2\,\mbox{.}$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| </div> | </div> | ||
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 6''' | '''Exempel 6''' | ||
| - | + | {| | |
| + | |- | ||
| + | | width=50% valign=top | | ||
| <ol type="a"> | <ol type="a"> | ||
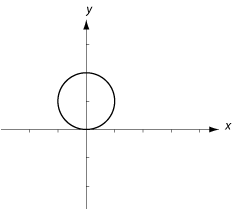
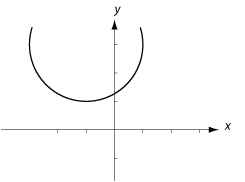
| <li>$(x-1)^2 + (y-2)^2 = 9\quad$ är ekvationen för en cirkel med medelpunkt i $\,(1,2)\,$ och radie $\,\sqrt{9} = 3\,$.<br><br> | <li>$(x-1)^2 + (y-2)^2 = 9\quad$ är ekvationen för en cirkel med medelpunkt i $\,(1,2)\,$ och radie $\,\sqrt{9} = 3\,$.<br><br> | ||
| + | </ol> | ||
| + | | width=45% valign=top | | ||
| + | [[Bild:t_3_2_12.gif|right]] | ||
| + | | width=5% valign=top | | ||
| + | |||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | width=50% valign=top | | ||
| + | <ol type="a" start=2> | ||
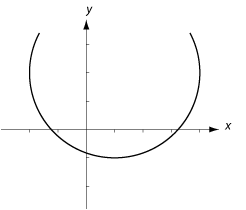
| <li>$x^2 + (y-1)^2 = 1\quad$ kan skrivas som $\,(x-0)^2 + (y-1)^2 = 1\,$ och är ekvationen för en cirkel med medelpunkt i $\,(0,1)\,$ och radie $\,\sqrt{1} = 1\,$.<br><br> | <li>$x^2 + (y-1)^2 = 1\quad$ kan skrivas som $\,(x-0)^2 + (y-1)^2 = 1\,$ och är ekvationen för en cirkel med medelpunkt i $\,(0,1)\,$ och radie $\,\sqrt{1} = 1\,$.<br><br> | ||
| - | <li>$(x+1)^2 + (y-3)^2 = 5\quad$ kan skrivas som $\,(x-(-1))^2 + (y-3)^2 = 5\,$ och är ekvationen för en cirkel med medelpunkt i $\,(-1,3)\,$ och radie $\,\sqrt{5} \approx 2{,}236\,$. | ||
| </ol> | </ol> | ||
| + | | width=45% valign=top | | ||
| + | [[Bild:t_3_2_13.gif|right]] | ||
| + | | width=5% valign=top | | ||
| - | Bild: figur 3.2-12-14 | + | |} |
| + | {| | ||
| + | |- | ||
| + | | width=60% valign=top | | ||
| + | <ol type="a" start=3> | ||
| + | <li>$(x+1)^2 + (y-3)^2 = 5\quad$ kan skrivas som $\,(x-(-1))^2 + (y-3)^2 = 5\,$ och är ekvationen för en cirkel med medelpunkt i $\,(-1,3)\,$ och radie $\,\sqrt{5} \approx 2{,}236\,$. | ||
| + | </ol> | ||
| + | | width=40% valign=top | | ||
| + | [[Bild:t_3_2_14.gif|right]] | ||
| + | |||
| + | |} | ||
| </div> | </div> | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 7''' | ||
| + | '''Exempel 7''' | ||
| + | {| | ||
| + | |- | ||
| + | | width=40% valign=top | | ||
| <ol type="a"> | <ol type="a"> | ||
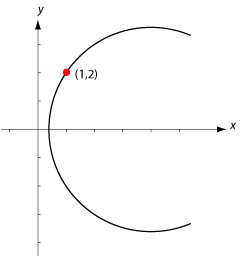
| <li>Ligger punkten $\,(1,2)\,$ på cirkeln $\,(x-4)^2 +y^2=13\,$?<br><br> | <li>Ligger punkten $\,(1,2)\,$ på cirkeln $\,(x-4)^2 +y^2=13\,$?<br><br> | ||
| - | Stoppar vi in punktens koordinater $\,x=1\,$ och $\,y=2\,$ i cirkelns ekvation har vi att | + | Stoppar vi in punktens koordinater $\,x=1\,$ och $\,y=2\,$ i cirkelns ekvation har vi att <br> |
| - | $$\mbox{VL }= (1-4)^2+2^2 =(-3)^2+2^2=9+4=13= \mbox{ HL}\,\mbox{.}$$ | + | $\mbox{VL }= (1-4)^2+2^2 = $ <br> |
| + | $=(-3)^2+2^2=9+4=13= \mbox{ HL}\,\mbox{.}$ <br> | ||
| Eftersom punkten uppfyller cirkelns ekvation ligger punken på cirkeln. <br><br> | Eftersom punkten uppfyller cirkelns ekvation ligger punken på cirkeln. <br><br> | ||
| + | </ol> | ||
| + | | width=60% valign=top | | ||
| + | [[Bild:t_3_2_15.gif|right]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | width=40% valign=top | | ||
| + | <ol type="a" start=2> | ||
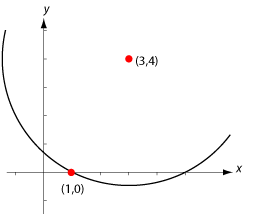
| <li>Bestäm ekvationen för cirkeln som har medelpunkt i $\,(3,4)\,$ och innehåller punkten $\,(1,0)\,$.<br><br> | <li>Bestäm ekvationen för cirkeln som har medelpunkt i $\,(3,4)\,$ och innehåller punkten $\,(1,0)\,$.<br><br> | ||
| Eftersom punkten $\,(1,0)\,$ ska ligga på cirkeln måste cirkelns radie vara lika med avståndet från $\,(1,0)\,$ till medelpunkten $\,(3,4)\,$. Avståndsformeln ger att detta avstånd är | Eftersom punkten $\,(1,0)\,$ ska ligga på cirkeln måste cirkelns radie vara lika med avståndet från $\,(1,0)\,$ till medelpunkten $\,(3,4)\,$. Avståndsformeln ger att detta avstånd är | ||
| Rad 195: | Rad 250: | ||
| $$(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}$$ | $$(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}$$ | ||
| </ol> | </ol> | ||
| - | + | | width=60% valign=top | | |
| - | Bild: 3.2.15 och 3.2.16 | + | [[Bild:t_3_2_16.gif|right]] |
| + | |} | ||
| </div> | </div> | ||
| + | |||
| <div class="exempel"> | <div class="exempel"> | ||
| Rad 235: | Rad 292: | ||
| '''Råd för inläsning''' | '''Råd för inläsning''' | ||
| - | '''Tänk på att:''' | + | '''Grund- och slutprov''' |
| + | Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge. | ||
| + | |||
| + | |||
| + | '''Tänk på att:''' | ||
| Rad 254: | Rad 315: | ||
| </div> | </div> | ||
| - | |||
| - | |||
| - | <small>© Copyright 2007, math.se</small> | ||
| - | |||
Nuvarande version
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|||||||||||||
[redigera] Teori[redigera] VinkelmåttDet finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer.
Exempel 1
I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än 360°. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv. Exempel 2
[redigera] AvståndsformelnPythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $\,a\,$ och $\,b\,$, och hypotenusa $\,c\,$ gäller att
Exempel 3 I triangeln till höger är $$c^2= 3^2 + 4^2 = 9 +16 = 25$$ och därför är hypotenusan $\,c\,$ lika med $$c=\sqrt{25} = 5\,\mbox{.}$$ Pythagoras sats kan användas för att beräkna avståndet mellan två punkter i ett koordinatsystem. Avståndsformeln: Avståndet $\,d\,$ mellan två punkter med koordinater $\,(x, y)\,$ och $\,(a, b)\,$ är $$d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}$$ Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna. Kateternas längd är lika med beloppet av skillnaden i x- och y-led mellan punkterna, dvs. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln. Exempel 4
[redigera] CirklarEn cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $\,r\,$ från en punkt $\,(a,b)\,$. Avståndet $\,r\,$ kallas för cirkelns radie och punkten $\,(a,b)\,$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp.
Exempel 5 En cirkelsektor är given i figuren till höger.
Exempel 6
Exempel 7
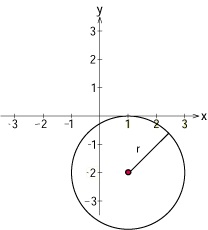
Exempel 8 Bestäm medelpunkt och radie för den cirkel vars ekvation är $\ x^2 + y^2 – 2x + 4y + 1 = 0\,$.
Börja med att kvadratkomplettera termerna som innehåller $\,x\,$ i vänsterledet $$ \underline{x^2-2x\vphantom{(}} + y^2+4y + 1 =\underline{(x-1)^2-1^2} + y^2+4y + 1$$ (de understrukna termerna visar kvadratkompletteringen). Kvadratkomplettera sedan termerna som innehåller $y$ $$ (x-1)^2-1^2 + \underline{y^2+4y} + 1= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}$$ Vänsterledet är alltså lika med $$ (x-1)^2 + (y+2)^2-4 $$ och flyttar vi över 4 till högerledet är cirkelns ekvation $$ (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}$$ Vi avläser att medelpunkten är $\,(1,-2)\,$ och radien är $\,\sqrt{4}= 2\,$.
Råd för inläsning Grund- och slutprov Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge.
för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om: Läs mer om Pythagoras sats på svenska Wikipedia Läs mer i Mathworld om cirkeln
Interaktivt experiment: sinus och cosinus i enehtscirkeln (Flash)
|
|