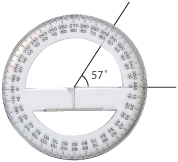
4.1 Vinklar och cirklar
Sommarmatte 1
| Versionen från 24 april 2007 kl. 09.34 (redigera) Lina (Diskussion | bidrag) ← Gå till föregående ändring |
Nuvarande version (25 maj 2007 kl. 15.18) (redigera) (ogör) Mikael (Diskussion | bidrag) (→Vinkelmått) |
||
| (66 mellanliggande versioner visas inte.) | |||
| Rad 1: | Rad 1: | ||
| + | __NOTOC__ | ||
| <table><tr><td width="600"> | <table><tr><td width="600"> | ||
| - | |||
| - | =4.1 Vinklar och cirklar= | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| '''Innehåll:''' | '''Innehåll:''' | ||
| - | *Vinkelmått | + | *Olika vinkelmått (grader, radianer och varv) |
| + | *Pythagoras sats | ||
| *Avståndsformeln i planet | *Avståndsformeln i planet | ||
| *Cirkelns ekvation | *Cirkelns ekvation | ||
| Rad 11: | Rad 11: | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| - | '''Läromål:''' | + | '''Lärandemål:''' |
| Efter detta avsnitt ska du ha lärt dig att: | Efter detta avsnitt ska du ha lärt dig att: | ||
| - | *Omvandla mellan grader, radianer och varv | + | *Omvandla mellan grader, radianer och varv. |
| - | *Beräkna arean och omkretsen av en cirkelsektor | + | *Beräkna arean och omkretsen av cirkelsektorer. |
| - | *Beräkna avståndet mellan två punkter i planet | + | *Känna till begreppen katet, hypotenusa och rätvinklig triangel. |
| - | *Skissera cirklar med hjälp av att kvadratkomplettera deras ekvationer | + | *Formulera och använda Pythagoras sats. |
| - | *Använda begreppen enhetscirkel, tangent, radie, diameter, pereferi, korda och cirkelbåge. | + | *Beräkna avståndet mellan två punkter i planet. |
| - | *Lösa geometriska problem som innehåller cirklar | + | *Skissera cirklar med hjälp av att kvadratkomplettera deras ekvationer. |
| + | *Känna till begreppen enhetscirkel, tangent, radie, diameter, periferi, korda och cirkelbåge. | ||
| + | *Lösa geometriska problem som innehåller cirklar. | ||
| </div> | </div> | ||
| Rad 35: | Rad 37: | ||
| =Teori= | =Teori= | ||
| - | ===Vinkelmått=== | + | ==Vinkelmått== |
| + | Det finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer. | ||
| + | *'''Grader.''' Om ett helt varv delas in i 360 delar, så kallas varje del 1 grad. Beteckningen för grader är $ ^\circ$. | ||
| - | För inte så länge sedan mätte man kortare sträckor i tum, och längre i fot eller meter. Dessa enheter är inte så lätta att översätta, men de användes för att de var praktiska i olika sammanhang. Av samma anledning finns det flera olika enheter för att mäta vinklar. | + | [[Bild:3_2_1.gif||center]] |
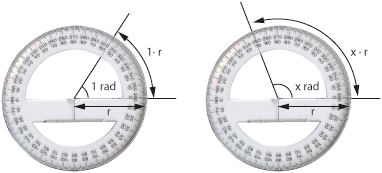
| + | *'''Radianer.''' Ett annat sätt att mäta vinklar är att använda längden av vinkelns cirkelbåge i förhållande till radien som mått på vinkeln. Detta vinkelmått kallas för radian. Ett varv är alltså $\,2\pi\,$ radianer eftersom cirkelns omkrets är $\,2\pi r\,$, där $\,r\,$ är cirkelns radie. | ||
| + | [[Bild:3_2_2.gif||center]] | ||
| - | Vinklar kan mätas på två principiellt olika sätt: | ||
| - | *Man kan dela in ett varv i delar. Om ett helt varv delas in i 360 delar, så kallas varje del en '''grad'''. Beteckningen för grader är $ ^\circ$. Om man delar in i 400 delar, kallas delen istället en '''gon''' eller en '''nygrad'''. Eftersom nygrader betecknas grad, måste man se upp så att man inte förväxlar dem med grader. Lantmätare behöver ibland bestämma vinklar med mycket hög noggrannhet. De kan använda vinkelenheterna c eller cc, vilka står för en hundradel av en gon, respektive en hundradel av en hundradel, dvs en tiotusendel. | + | Ett helt varv är $\,360^\circ\,$ eller $\,2\pi\,$ radianer och det gör att |
| - | *Man kan även använda en längdskala för att mäta vinklar, om man mäter sträckan över vinkeln längs periferin av en cirkel. Eftersom omkretsen av en cirkel är $2\pi r$, så är det praktiskt att välja cirkelns radie som längdenhet. Då blir ett varv alltid $2\pi$ längdenheter, oavsett hur stor cirkeln är. Detta vinkelmått kallas '''radianer'''. Ett varv är alltså $2\pi$ radianer. Radianer betecknas rad, eller skrivs helt utan beteckning. | + | $$\eqalign{&1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radianer } = \frac{\pi}{180}\ \mbox{ radianer,}\cr &1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ = \frac{180^\circ}{\pi}\,\mbox{.}}$$ |
| + | Dessa omvandlingsfaktorer kan användas för att konvertera mellan grader och radianer. | ||
| + | <div class="exempel"> | ||
| + | '''Exempel 1''' | ||
| + | <ol type="a"> | ||
| + | <li>$30^\circ = 30 \cdot 1^\circ = 30 \cdot \displaystyle \frac{\pi}{180}\ \mbox{ radianer } = \displaystyle \frac{\pi}{6}\ \mbox{ radianer }$ <br><br> | ||
| + | <li>$ \displaystyle \frac{\pi}{8}\ \mbox { radianer } = \displaystyle \frac{\pi}{8} \cdot (1 \; \mbox{radian}\,) = \displaystyle \frac{\pi}{8} \cdot \displaystyle \frac{180^\circ}{\pi} = 22{,}5^\circ$ | ||
| + | </ol> | ||
| - | <img src="object49972/bilder/3_2/3_2_01.gif"> | + | </div> |
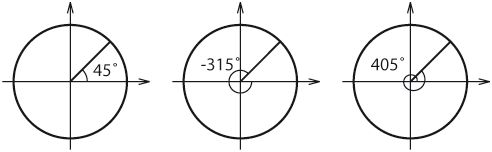
| + | I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än 360°. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv. | ||
| - | Eftersom längden på omkretsen av en cirkel är $2\pi \;$ multiplicerat med radiens längd så går det $2\pi \approx 6,28$ radianer på ett helt varv. | + | [[Bild:t_3_2_4.gif|center]] |
| + | <div class="exempel"> | ||
| + | '''Exempel 2''' | ||
| + | <ol type="a"> | ||
| + | <li>Vinklarna $\,-55^\circ\,$ och $\,665^\circ\,$ anger samma riktning eftersom | ||
| + | $$-55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}$$ | ||
| + | <li>Vinklarna $\,\displaystyle\frac{3\pi}{7}\,$ och $\,-\displaystyle\frac{11\pi}{7}\,$ anger samma riktning eftersom | ||
| + | $$\frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}$$ | ||
| - | I denna kurs kommer vi främst att använda vinkelmåtten grader och radianer. Grader används mest i vardagliga sammanhang och inom geometri, eftersom viktiga vinklar blir hela tal. Vinkeln $90^\circ$ är en rät vinkel. Vinklarna i den liksidiga triangeln är $60^\circ$. | + | <li> Vinklarna $\,36^\circ\,$ och $\,216^\circ\,$ anger inte samma riktning utan motsatta riktningar eftersom |
| + | $$36^\circ + 180^\circ = 216^\circ\,\mbox{.}$$ | ||
| + | </ol> | ||
| - | Nygrader kan vara praktiska att räkna med, eftersom de mest påminner om vårt vanliga talsystem där vi använder basen 10. En rät vinkel är 100 grad. Vinklarna i den liksidiga triangeln, som är $60^\circ$, blir däremot krångliga. De blir 200/3 grad = 66,6666... grad. För en lantmätare spelar detta ingen större roll. Lantmätaren har så gott som aldrig en vinkel som är exakt $60^\circ$. | + | </div> |
| - | Radianer används gärna inom matematik och fysik. De har fördelen att derivering och integrering av de trigonometriska funktionerna blir enkel. Derivatan av $\sin{x}$ blir $\cos{x}$ om man använder radianer som vinkelmått. Om man anger vinkeln ''x'' i grader får man istället att derivatan av $\sin{x}$ blir $\displaystyle\frac{\pi}{180}\cdot \cos {x}$. | + | ==Avståndsformeln== |
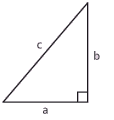
| + | Pythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $\,a\,$ och $\,b\,$, och hypotenusa $\,c\,$ gäller att | ||
| - | I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än $360^\circ$, t.ex. när vinkeln representerar en vridning till en viss riktning. Då kan man använda att man kan nå samma riktning genom flera olika vridningar, t.ex. genom att lägga till ett eller flera hela varv. Exempelvis anger vinklarna $–30^\circ, 330^\circ$ och $690^\circ$ samma riktning. | + | <div class="regel"> |
| - | <p align="center"><img src="ppStdFiles2261/820351.gif" hspace='0' vspace='0' /><br clear='all' /> | + | [[Bild:T_3_2_5.gif|right]] |
| + | '''Pythagoras sats:''' | ||
| + | $$c^2 = a^2 + b^2\,\mbox{.}$$ | ||
| Rad 71: | Rad 96: | ||
| - | Några viktiga vinklar som är bra att kunna översätta till utantill mellan grader och radianer.<p align="left"><img src="ppStdFiles2261/774115.gif" hspace='0' vspace='0' /><br clear='all' /> | + | </div> |
| - | [http://www.math.kth.se/online/images/sinus_och_cosinus_i_enhetscirkeln.swf Interaktivt experiment: sinus och cosinus i enehtscirkeln] (Flash) | + | |
| - | Omvandlingsfaktorn mellan radianer och grader kan man få ur sambanden | + | <div class="exempel"> |
| - | 1 varv = $360^\circ$ = $2\pi$ rad | + | '''Exempel 3''' |
| + | [[Bild:3_2_6.gif|right]] | ||
| + | I triangeln till höger är | ||
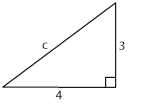
| + | $$c^2= 3^2 + 4^2 = 9 +16 = 25$$ | ||
| + | och därför är hypotenusan $\,c\,$ lika med | ||
| + | $$c=\sqrt{25} = 5\,\mbox{.}$$ | ||
| - | 1 rad = $\displaystyle\frac{360^\circ}{2\pi} = \displaystyle\frac{180^\circ}{\pi} \approx 57,295^\circ$ | + | </div> |
| + | Pythagoras sats kan användas för att beräkna avståndet mellan två punkter i ett koordinatsystem. | ||
| + | <div class="regel"> | ||
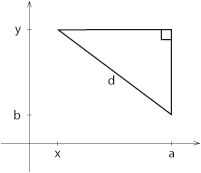
| + | '''Avståndsformeln:''' | ||
| + | Avståndet $\,d\,$ mellan två punkter med koordinater $\,(x, y)\,$ och $\,(a, b)\,$ är | ||
| + | $$d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}$$ | ||
| + | </div> | ||
| - | ===Cirkelsektorer och båglängder=== | + | Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna. |
| + | [[Bild:3_2_7.gif|center]] | ||
| - | <img src="object49972/bilder/3_2/3_2_04.gif" align="right">Om vi har öppningsvinkeln $\alpha$ för en cirkelsektor kan vi beräkna cirkelsektorns area ''A'' och cirkelbågens båglängd b, genom att betrakta dem som en andel av en hel cirkel. | + | Kateternas längd är lika med beloppet av skillnaden i ''x''- och ''y''-led mellan punkterna, dvs. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln. |
| - | Eftersom en hel cirkel har omkretsen $2\pi r$ och arean $\pi r^2$, får vi | + | <div class="exempel"> |
| + | '''Exempel 4''' | ||
| - | bågens längd utefter cirkelsektorn $= b = \displaystyle\frac{\alpha}{2\pi} 2\pi r = \alpha r$ | + | <ol type="a"> |
| + | <li>Avståndet mellan $\,(1,2)\,$ och $\,(3,1)\,$ är | ||
| + | $$d=\sqrt{ (1-3)^2 + (2-1)^2} = \sqrt{(-2)^2 + 1^2} = \sqrt{ 4+1} = \sqrt{5}\,\mbox{.}$$ | ||
| - | arean $= A = \displaystyle\frac{\alpha}{2\pi} \pi r^2 = \displaystyle\frac{\alpha r^2}{2}$ | + | <li>Avståndet mellan $\,(-1,0)\,$ och $\,(-2,-5)\,$ är |
| + | $$d=\sqrt{ (-1-(-2))^2 + (0-(-5))^2} = \sqrt{1^2 + 5^2} = \sqrt{1+25} = \sqrt{26}\,\mbox{.}$$ | ||
| + | </ol> | ||
| - | Observera att vinkeln $\alpha$ måste anges i radianer för att formlerna skall bli så snygga. | + | </div> |
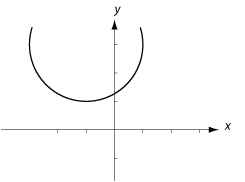
| + | ==Cirklar== | ||
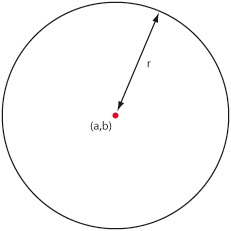
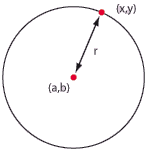
| + | En cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $\,r\,$ från en punkt $\,(a,b)\,$. | ||
| + | [[Bild:3_2_8.gif|center]] | ||
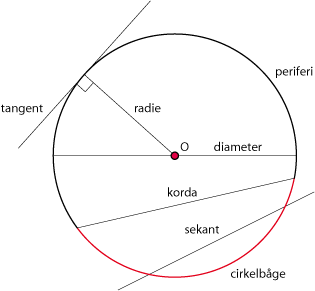
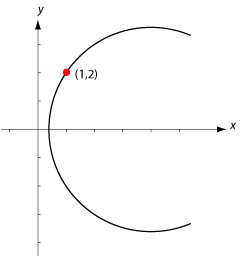
| - | ===Pythagoras sats, avståndsformeln och cirkels ekvation=== | + | Avståndet $\,r\,$ kallas för cirkelns radie och punkten $\,(a,b)\,$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp. |
| + | [[Bild:3_2_10.gif|center]] | ||
| - | <img src="object49972/bilder/3_2/3_2_05.gif" align="right">Pythagoras sats gäller för alla rätvinkliga trianglar. Satsen säger att summan av kateternas kvadrater är lika med kvadraten på hypotenusan, dvs $A^2 + B^2 = C^2$ | + | <div class="exempel"> |
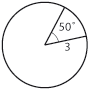
| + | '''Exempel 5''' | ||
| + | En cirkelsektor är given i figuren till höger. [[Bild:t_3_2_9.gif|right]] | ||
| + | <ol type="a"> | ||
| + | <li>Bestäm cirkelbågens längd. <br><br> | ||
| + | Medelpunktsvinkeln $\,50^\circ\,$ blir i radianer | ||
| + | $$50^\circ= 50 \cdot 1^\circ = 50 \cdot \frac{\pi}{180}\ \mbox{ radianer } = \frac{5\pi}{18}\ \mbox{ radianer. }$$ | ||
| + | På det sätt som radianer är definierat betyder detta att cirkelbågens längd är radien multiplicerat med vinkeln mätt i radianer, | ||
| + | $$3 \cdot \frac{5\pi}{18}\ \mbox{ l.e. } = \frac{5\pi}{6}\ \mbox{ l.e. }$$ | ||
| + | <li>Bestäm cirkelsektorns area. <br><br> | ||
| + | Cirkelsektorns andel av hela cirkeln är $$\frac{50^\circ}{360^\circ} = \frac{5}{36}$$ | ||
| + | och det betyder att dess area är $\,\frac{5}{36}\,$ delar av cirkelns area som är $\,\pi r^2 = \pi 3^2 = 9\pi\,$, dvs. | ||
| + | $$\frac{5}{36} \cdot 9\pi\ \mbox{ a.e. }= \frac{5\pi}{4}\ \mbox{ a.e. }$$ | ||
| + | </ol> | ||
| - | (Även omvändningen av satsen gäller, d.v.s. om $A^2 + B^2 = C^2$ så är triangeln rätvinklig.) | + | </div> |
| + | En punkt $\,(x,y)\,$ ligger på cirkeln som har medelpunkt i $\,(a,b)\,$ och radie $\,r\,$ om dess avstånd till medelpunkten är lika med $\,r\,$. Detta villkor kan formuleras med avståndsformeln som | ||
| + | <div class="regel"> | ||
| + | [[Bild:T_3_2_11.gif|right]] | ||
| + | '''Cirkelns ekvation:''' | ||
| + | $$(x – a)^2 + (y – b)^2 = r^2\,\mbox{.}$$ | ||
| Rad 114: | Rad 177: | ||
| - | <img src="object49972/bilder/3_2/3_2_06.gif" align="right">Pythagoras sats kan användas för att beräkna avståndet mellan två punkter i ett koordinatsystem. Om punkterna har koordinaterna ''(x, y)'' och ''(a, b)'' och vi kallar avståndet mellan punkterna för ''d'', så får vi den så kallade avståndsformeln | ||
| - | $d = \sqrt{(x – a)^2 + (y – b)^2} $. | ||
| - | [http://www.theducation.se/kurser/experiment/gyma/applets/ex24_avstand_pythagoras/index.html | + | </div> |
| - | Interaktivt experiment: Här kan du experimentera med avståndsformeln och Pythagoras sats | + | |
| - | ] | + | <div class="exempel"> |
| - | ---- | + | '''Exempel 6''' |
| + | {| | ||
| + | |- | ||
| + | | width=50% valign=top | | ||
| + | <ol type="a"> | ||
| + | <li>$(x-1)^2 + (y-2)^2 = 9\quad$ är ekvationen för en cirkel med medelpunkt i $\,(1,2)\,$ och radie $\,\sqrt{9} = 3\,$.<br><br> | ||
| + | </ol> | ||
| + | | width=45% valign=top | | ||
| + | [[Bild:t_3_2_12.gif|right]] | ||
| + | | width=5% valign=top | | ||
| + | |} | ||
| + | {| | ||
| + | |- | ||
| + | | width=50% valign=top | | ||
| + | <ol type="a" start=2> | ||
| + | <li>$x^2 + (y-1)^2 = 1\quad$ kan skrivas som $\,(x-0)^2 + (y-1)^2 = 1\,$ och är ekvationen för en cirkel med medelpunkt i $\,(0,1)\,$ och radie $\,\sqrt{1} = 1\,$.<br><br> | ||
| + | </ol> | ||
| + | | width=45% valign=top | | ||
| + | [[Bild:t_3_2_13.gif|right]] | ||
| + | | width=5% valign=top | | ||
| - | ===Definition av en cirkel=== | + | |} |
| - | <img src="object49972/bilder/3_2/3_2_08.gif" align="right"> | + | {| |
| + | |- | ||
| + | | width=60% valign=top | | ||
| + | <ol type="a" start=3> | ||
| + | <li>$(x+1)^2 + (y-3)^2 = 5\quad$ kan skrivas som $\,(x-(-1))^2 + (y-3)^2 = 5\,$ och är ekvationen för en cirkel med medelpunkt i $\,(-1,3)\,$ och radie $\,\sqrt{5} \approx 2{,}236\,$. | ||
| + | </ol> | ||
| + | | width=40% valign=top | | ||
| + | [[Bild:t_3_2_14.gif|right]] | ||
| - | En cirkel kan definieras som mängden av alla punkter ''(x, y)'' som ligger på ett visst avstånd ''r'' från en given punkt ''(a, b)''. Avståndet ''r'' blir då cirkels radie, och punkten ''(a, b)'' blir cirkelns medelpunkt. Detta ger med hjälp av avståndsformeln villkoret | + | |} |
| - | + | ||
| - | + | ||
| - | + | ||
| - | $r = \sqrt{(x – a)^2 + (y – b)^2}$. | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | Detta villkor brukar genom kvadrering skrivas | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | $(x – a)^2 + (y – b)^2 = r^2$ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | och kallas för '''cirkelns ekvation'''. | + | |
| - | Cirkeln är alltså mängden av alla punkter $(x, y)$ som uppfyller ekvationen | + | |
| - | $(x – a)^2 + (y – b)^2 = r^2$ och ligger på avståndet ''r'' från punkten $(a, b)$. | + | |
| - | Om man sätter ''r'' = 1 och $(a,b) = (0,0)$ får man en cirkel med radien 1 och medelpunkten i origo. Denna cirkel kallas enhetscirkeln. | + | |
| - | Enhetscirkeln är ett viktigt hjälpmedel i många sammanhang, t.ex. när man arbetar med trigonometriska funktioner. | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | <div class="tips"> | + | |
| - | '''Några fakta om cirklar''' | + | |
| - | + | ||
| - | *Arean av en cirkel med radie $r$ är $\pi r^2$. | + | |
| - | *Omkretsen av en cirkel med radie $r$'' är ''$2\pi r$. | + | |
| - | *Radien är avståndet från cirkelns medelpunkt till en punkt på periferin. | + | |
| - | *Några andra viktiga geometriska begrepp för cirkeln visas i figuren | + | |
| </div> | </div> | ||
| + | <div class="exempel"> | ||
| + | '''Exempel 7''' | ||
| + | {| | ||
| + | |- | ||
| + | | width=40% valign=top | | ||
| + | <ol type="a"> | ||
| + | <li>Ligger punkten $\,(1,2)\,$ på cirkeln $\,(x-4)^2 +y^2=13\,$?<br><br> | ||
| + | Stoppar vi in punktens koordinater $\,x=1\,$ och $\,y=2\,$ i cirkelns ekvation har vi att <br> | ||
| + | $\mbox{VL }= (1-4)^2+2^2 = $ <br> | ||
| + | $=(-3)^2+2^2=9+4=13= \mbox{ HL}\,\mbox{.}$ <br> | ||
| + | Eftersom punkten uppfyller cirkelns ekvation ligger punken på cirkeln. <br><br> | ||
| + | </ol> | ||
| + | | width=60% valign=top | | ||
| + | [[Bild:t_3_2_15.gif|right]] | ||
| + | |} | ||
| - | '''Några viktiga begrepp''' | ||
| + | {| | ||
| + | |- | ||
| + | | width=40% valign=top | | ||
| + | <ol type="a" start=2> | ||
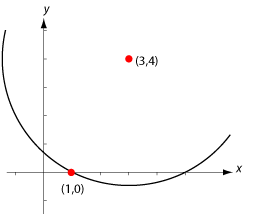
| + | <li>Bestäm ekvationen för cirkeln som har medelpunkt i $\,(3,4)\,$ och innehåller punkten $\,(1,0)\,$.<br><br> | ||
| + | Eftersom punkten $\,(1,0)\,$ ska ligga på cirkeln måste cirkelns radie vara lika med avståndet från $\,(1,0)\,$ till medelpunkten $\,(3,4)\,$. Avståndsformeln ger att detta avstånd är | ||
| + | $$c=\sqrt{(3-1)^2 + (4-0)^2 }= \sqrt{4 +16} = \sqrt{20} \, \mbox{.}$$ | ||
| + | Cirkelns ekvation är därför | ||
| + | $$(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}$$ | ||
| + | </ol> | ||
| + | | width=60% valign=top | | ||
| + | [[Bild:t_3_2_16.gif|right]] | ||
| + | |} | ||
| - | <img src="object49972/bilder/3_2/3_2_10.gif"> | ||
| - | |||
| - | Det är inte alltid helt enkelt att känna igen ekvationen för en cirkel. Med hjälp av kvadratkomplettering (tidigare presenterat i avsnitt 2.3) kan man skriva ekvationen på så kallad '''standardform''', där går det direkt att avläsa cirkelns radie och medelpunkt. | ||
| - | |||
| - | |||
| - | <div class="exempel"> | ||
| - | '''Exempel 1''' | ||
| - | |||
| - | Skissera cirkeln | ||
| - | $ x^2 + y^2 = 4$ | ||
| - | |||
| - | '''Lösning:''' | ||
| - | |||
| - | Vi jämför den aktuella cirkeln med '''cirkelns ekvation'''. | ||
| - | $(x-x_0)^2+(y-y_0)^2=r^2$ | ||
| - | Vi ser att i vårt fall är | ||
| - | $x_0=0$ och $y_0=0$ | ||
| - | Detta betyder alltså att cirkeln har sin medelpunkt i $(0,0)$ dvs i origo. | ||
| - | Radien på cirkeln går att avläsa ur högerledet: | ||
| - | $r = \sqrt {r^2} = \sqrt 4 = 2$ | ||
| - | Med denna information kan vi skissera cirkeln enligt nedan.<p align="center"><img src="ppStdFiles2261/766791.gif" hspace='0' vspace='0' /><br clear='all' /> | ||
| </div> | </div> | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 2''' | + | '''Exempel 8''' |
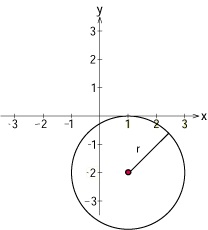
| - | Bestäm medelpunkten för den cirkel vars ekvation är $x^2 + y^2 – 2x + 4y + 1 = 0$. | + | Bestäm medelpunkt och radie för den cirkel vars ekvation är $\ x^2 + y^2 – 2x + 4y + 1 = 0\,$. |
| + | Vi ska försöka skriva om cirkelns ekvation på formen | ||
| + | $$(x – a)^2 + (y – b)^2 = r^2$$ | ||
| + | för då kan vi direkt avläsa att medelpunken är $\,(a,b)\,$ och radien är $\,r\,$. | ||
| - | '''Lösning:''' | + | Börja med att kvadratkomplettera termerna som innehåller $\,x\,$ i vänsterledet |
| + | $$ \underline{x^2-2x\vphantom{(}} + y^2+4y + 1 =\underline{(x-1)^2-1^2} + y^2+4y + 1$$ | ||
| + | (de understrukna termerna visar kvadratkompletteringen). | ||
| - | Vi försöker skriva om på normalformen av cirkelns ekvation, | + | Kvadratkomplettera sedan termerna som innehåller $y$ |
| - | $(x-x_0)^2+(y-y_0)^2=r^2$, där $(x_0,y_0)$ är centrum och $r$ är radien. | + | $$ (x-1)^2-1^2 + \underline{y^2+4y} + 1= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}$$ |
| + | Vänsterledet är alltså lika med | ||
| + | $$ (x-1)^2 + (y+2)^2-4 $$ | ||
| + | och flyttar vi över 4 till högerledet är cirkelns ekvation | ||
| + | $$ (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}$$ | ||
| - | Vi utgår från de termer som innehåller $x\;$, nämligen $\; x^2-2x$ | + | Vi avläser att medelpunkten är $\,(1,-2)\,$ och radien är $\,\sqrt{4}= 2\,$. |
| + | [[Bild:766790.gif||center]] | ||
| + | </div> | ||
| - | och skriver om den m.h.a. andra kvadreringsregeln, | + | [[4.1 Övningar|Övningar]] |
| + | <div class="inforuta"> | ||
| + | '''Råd för inläsning''' | ||
| - | $ a^2-2ab+b^2=(a-b)^2 $ | + | '''Grund- och slutprov''' |
| + | Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge. | ||
| - | |||
| - | Vi identifierar $ a=x $ och $ b=1 $ vilket ger $ b^2=1 $, vi har då | ||
| - | |||
| - | |||
| - | |||
| - | $ x^2-2x=(x-1)^2-1 $ | ||
| - | |||
| - | |||
| - | |||
| - | På samma sätt får vi för termerna $ y^2 + 4y $ | ||
| - | |||
| - | |||
| - | |||
| - | $ y^2+4y=(y+2)^2-4 $ | ||
| - | |||
| - | |||
| - | |||
| - | Vår ursprungliga ekvation $ x^2+y^2-2x+4y+1=0 $ kan då skrivas som | ||
| - | |||
| - | |||
| - | |||
| - | $ (x-1)^2-1+(y+2)^2-4+1=0 $ | ||
| - | |||
| - | |||
| - | |||
| - | vilket förenklas till | ||
| - | |||
| - | |||
| - | |||
| - | $ (x-1)^2 + (y+2)^2 = 4 $ | ||
| - | |||
| - | |||
| - | |||
| - | Vi jämför med cirkelns ekvation på normalform och identifierar medelpunkten $ (x_0,y_0)=(1,-2) $ samt radien $ \sqrt{4}=2 $ . | ||
| - | |||
| - | |||
| - | |||
| - | Denna information behövs om du vill rita figuren, utgå då från medelpunkt och radie enligt ovan.<p align="center"><img src="ppStdFiles2261/766790.gif" hspace='0' vspace='0' /><br clear='all' /> | ||
| - | |||
| - | |||
| - | '''Svar:''' medelpunkten är $ (1,-2) $ | ||
| - | |||
| - | </div> | ||
| - | |||
| - | |||
| - | <div class="inforuta"> | ||
| - | '''Råd för inläsning''' | ||
| '''Tänk på att:''' | '''Tänk på att:''' | ||
| - | |||
| - | Lär dig att använda enhetscirkeln som ett verktyg i det trigonometriska arbetet. Avläsningar i enhetscirkeln ger dig viktiga upplysningar om diverse samband. | ||
| Rad 277: | Rad 303: | ||
| för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om: | för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om: | ||
| - | |||
| - | [http://www.theducation.se/kurser/gymab/bgeometri_sam/bgeometri_sam.htm Sammanfattning av Geometri B ur Theducations gymnasielexikon] | ||
| [http://sv.wikipedia.org/wiki/Pythagoras_sats Läs mer om Pythagoras sats på svenska Wikipedia] | [http://sv.wikipedia.org/wiki/Pythagoras_sats Läs mer om Pythagoras sats på svenska Wikipedia] | ||
| Rad 287: | Rad 311: | ||
| '''Länktips''' | '''Länktips''' | ||
| - | [http://www.theducation.se/kurser/experiment/gyma/applets/ex31_randvinkelsatsen/index.html Experimentera med Randvinkelsatsen] | + | [http://www.math.kth.se/online/images/sinus_och_cosinus_i_enhetscirkeln.swf Interaktivt experiment: sinus och cosinus i enehtscirkeln] (Flash) |
| - | [http://www.theducation.se/kurser/experiment/gyma/applets/ex24_avstand_pythagoras/index.html Experimentera med Pythagoras sats] | ||
| - | |||
| - | [http://www.theducation.se/kurser/experiment/gyma/applets/ex38_fyrhorning/fyrhorning.html Experimentera med vinkelsumman i en fyrhörning] | ||
| </div> | </div> | ||
| - | |||
| - | |||
| - | '''© Copyright 2006, KTH Matematik''' | ||
| - | |||
Nuvarande version
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|||||||||||||
[redigera] Teori[redigera] VinkelmåttDet finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer.
Exempel 1
I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än 360°. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv. Exempel 2
[redigera] AvståndsformelnPythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $\,a\,$ och $\,b\,$, och hypotenusa $\,c\,$ gäller att
Exempel 3 I triangeln till höger är $$c^2= 3^2 + 4^2 = 9 +16 = 25$$ och därför är hypotenusan $\,c\,$ lika med $$c=\sqrt{25} = 5\,\mbox{.}$$ Pythagoras sats kan användas för att beräkna avståndet mellan två punkter i ett koordinatsystem. Avståndsformeln: Avståndet $\,d\,$ mellan två punkter med koordinater $\,(x, y)\,$ och $\,(a, b)\,$ är $$d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}$$ Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna. Kateternas längd är lika med beloppet av skillnaden i x- och y-led mellan punkterna, dvs. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln. Exempel 4
[redigera] CirklarEn cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $\,r\,$ från en punkt $\,(a,b)\,$. Avståndet $\,r\,$ kallas för cirkelns radie och punkten $\,(a,b)\,$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp.
Exempel 5 En cirkelsektor är given i figuren till höger.
Exempel 6
Exempel 7
Exempel 8 Bestäm medelpunkt och radie för den cirkel vars ekvation är $\ x^2 + y^2 – 2x + 4y + 1 = 0\,$.
Börja med att kvadratkomplettera termerna som innehåller $\,x\,$ i vänsterledet $$ \underline{x^2-2x\vphantom{(}} + y^2+4y + 1 =\underline{(x-1)^2-1^2} + y^2+4y + 1$$ (de understrukna termerna visar kvadratkompletteringen). Kvadratkomplettera sedan termerna som innehåller $y$ $$ (x-1)^2-1^2 + \underline{y^2+4y} + 1= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}$$ Vänsterledet är alltså lika med $$ (x-1)^2 + (y+2)^2-4 $$ och flyttar vi över 4 till högerledet är cirkelns ekvation $$ (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}$$ Vi avläser att medelpunkten är $\,(1,-2)\,$ och radien är $\,\sqrt{4}= 2\,$.
Råd för inläsning Grund- och slutprov Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge.
för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om: Läs mer om Pythagoras sats på svenska Wikipedia Läs mer i Mathworld om cirkeln
Interaktivt experiment: sinus och cosinus i enehtscirkeln (Flash)
|
|