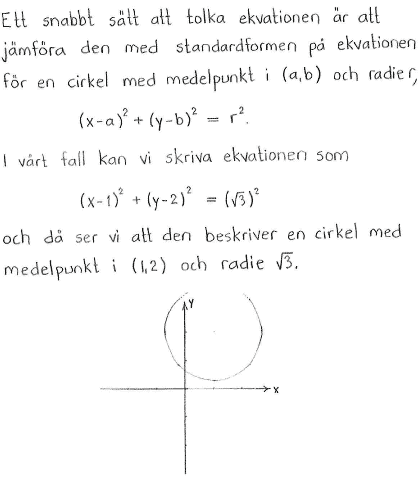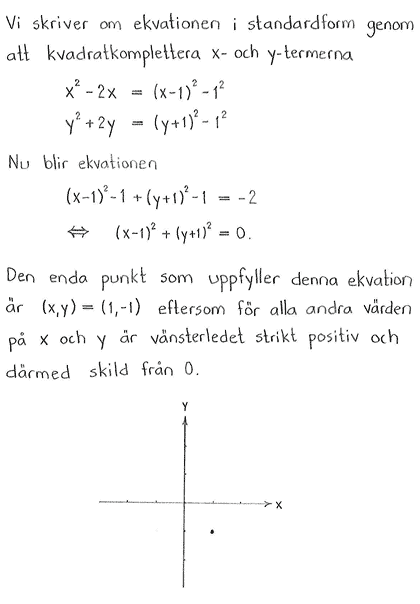4.1 Övningar
Sommarmatte 1
| Versionen från 29 april 2007 kl. 13.28 (redigera) Annagf (Diskussion | bidrag) (→Övning 4.1:8) ← Gå till föregående ändring |
Versionen från 29 april 2007 kl. 13.35 (redigera) (ogör) Annagf (Diskussion | bidrag) (→Övning 4.1:8) Gå till nästa ändring → |
||
| Rad 466: | Rad 466: | ||
| <div class=NavContent> | <div class=NavContent> | ||
| <br />[[Bild:4_1_8.gif]] | <br />[[Bild:4_1_8.gif]] | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | ==Övning 4.1:9== | ||
| + | <div class="ovning"> | ||
| + | På en klocka är sekundvisaren 8 cm lång. Hur stor area sveper den över på 10 sekunder? | ||
| + | </div> | ||
| + | |||
| + | <div class=NavFrame style="CLEAR: both"> | ||
| + | <div class=NavHead>Facit </div> | ||
| + | <div class=NavContent> | ||
| + | $\displaystyle \frac{32\pi}{3} \textrm{ cm}^2 \approx 33,5 \textrm{ cm}^2$ | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | <div class=NavFrame style="CLEAR: both"> | ||
| + | <div class=NavHead>Lösning </div> | ||
| + | <div class=NavContent> | ||
| + | <br />[[Bild:4_1_9.gif]] | ||
| </div> | </div> | ||
| </div> | </div> | ||
Versionen från 29 april 2007 kl. 13.35
Innehåll |
Övning 4.1:1
Skriv i grader och radianer
| $\textrm{a) }$ | $\displaystyle \frac{1}{4} \textrm{ varv} $ | $\textrm{b) }$ | $\displaystyle \frac{3}{8} \textrm{ varv}$ | $\textrm{c) }$ | $-\displaystyle \frac{2}{3}\textrm{ varv}$ | $\textrm{d) }$ | $\displaystyle \frac{97}{12} \textrm{ varv} $ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $90^\circ, \displaystyle \frac{\pi}{2} \textrm{ rad} $ | $\textrm{b) }$ | $135^\circ,\displaystyle \frac{3\pi}{4} \textrm{ rad}$ | $\textrm{c) }$ | $-240^\circ, \displaystyle \frac{-4\pi}{3} \textrm{ rad}$ | $\textrm{d) }$ | $2910^\circ, \displaystyle \frac{97\pi}{6} \textrm{ rad}$ |
Lösning till delfråga a
Bild:4 1 1a.gif
Lösning till delfråga b
Bild:4 1 1b.gif
Lösning till delfråga c
Bild:4 1 1c.gif
Lösning till delfråga d
Bild:4 1 1d.gif
Övning 4.1:2
Omvandla till radianer
| $\textrm{a) }$ | $45^\circ$ | $\textrm{b) }$ | $135^\circ$ | $\textrm{c) }$ | $-63^\circ$ | $\textrm{d) }$ | $270^\circ$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $\displaystyle \frac{\pi}{4}\textrm{ rad}$ | $\textrm{b) }$ | $\displaystyle \frac{3\pi}{4}\textrm{ rad}$ | $\textrm{c) }$ | $-\displaystyle \frac{7\pi}{20}\textrm{ rad}$ | $\textrm{d) }$ | $\displaystyle \frac{3\pi}{2}\textrm{ rad}$ |
Lösning till delfråga a
Bild:4 1 2a.gif
Lösning till delfråga b
Bild:4 1 2b.gif
Lösning till delfråga c
Bild:4 1 2c.gif
Lösning till delfråga d
Bild:4 1 2d.gif
Övning 4.1:3
Bestäm längden av sidan som är markerad med $x$
| a) | BILD | b) | BILD | c) | BILD |
Facit till alla delfrågorna
| a) | $x=50$ | b) | $x=5$ | c) | $x=15$ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Övning 4.1:4
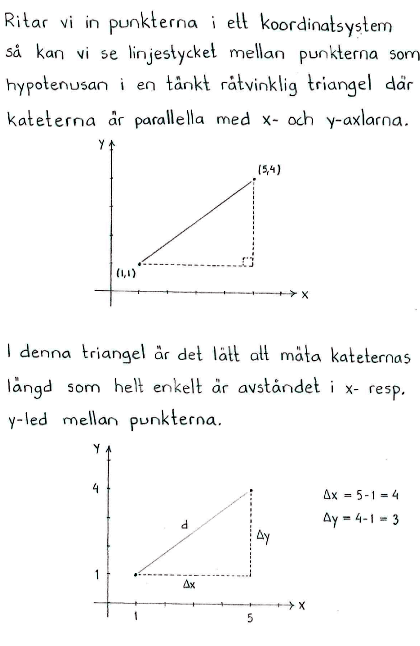
| $\textrm{a) }$ | Bestäm avståndet mellan punkterna (1,1) och (5,4) |
| $\textrm{b) }$ | Bestäm avståndet mellan punkterna (-2,5) och (3,-1) |
| $\textrm{c) }$ | Hitta den punkt på x-axeln som ligger lika långt från punkterna (3,3) och (5,1) |
Facit till alla delfrågorna
| $\textrm{a) }$ | $5 \textrm{ l.e.}$ |
| $\textrm{b) }$ | $\sqrt{61} \textrm{ l.e.}$ |
| $\textrm{c) }$ | $(2,0)$ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Bild:4 1 4c.gif
Övning 4.1:5
| $\textrm{a) }$ | Bestäm ekvationen för en cirkel med medelpunkt i (1,2) och radie 2 |
| $\textrm{b) }$ | Bestäm ekvationen för den cirkel som har medelpunkt i (2,-1) och innehåller punkten (-1,1) |
Facit till alla delfrågorna
| $\textrm{a) }$ | $(x-1)^2+(y-2)^2=4$ |
| $\textrm{b) }$ | $(x-2)^2+(y+1)^2=13$ |
Lösning till delfråga a
Lösning till delfråga b
Bild:4 1 5b.gif
Övning 4.1:6
Skissera följande cirklar
| $\textrm{a) }$ | $x^2+y^2=9$ | $\textrm{b) }$ | $(x-1)^2+(y-2)^2=3$ | $\textrm{c) }$ | $(3x-1)^2+(3y+7)^2=10$ |
Facit till alla delfrågorna
| a) | BILD |
| b) | BILD |
| c) | BILD |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga b
Bild:4 1 6c.gif
Övning 4.1:7
Skissera följande cirklar
| a) | $x^2+2x+y^2-2y=1$ | b) | $x^2+y^2+4y=0$ | c) | $x^2-2x+y^2+6y=-3$ |
| d) | $x^2-2x+y^2+2y=-2$ | ||||
Facit till alla delfrågorna
| a) | BILD |
| b) | BILD |
| c) | BILD |
| d) | BILD |
Lösning till delfråga a
Bild:4 1 7a.gif
Lösning till delfråga b
Lösning till delfråga b
Lösning till delfråga b
Övning 4.1:8
Hur många varv snurrar ett hjul med radie 50 cm när det rullar 10m?
$\displaystyle \frac{10}{\pi}\textrm{ varv }\approx 3,2 \textrm{ varv} $
Övning 4.1:9
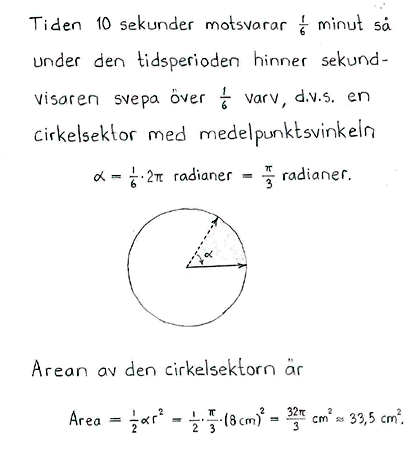
På en klocka är sekundvisaren 8 cm lång. Hur stor area sveper den över på 10 sekunder?
$\displaystyle \frac{32\pi}{3} \textrm{ cm}^2 \approx 33,5 \textrm{ cm}^2$
