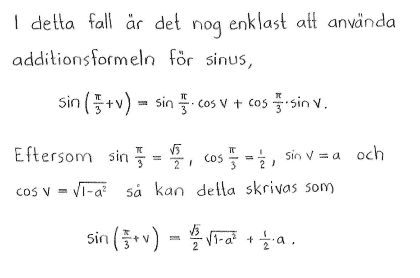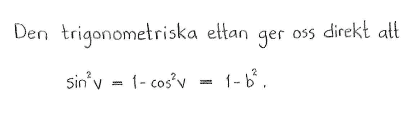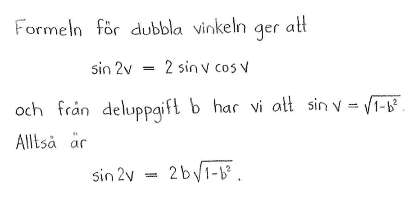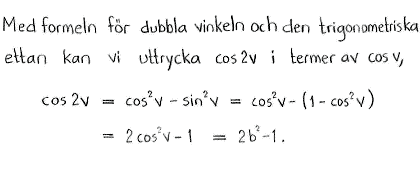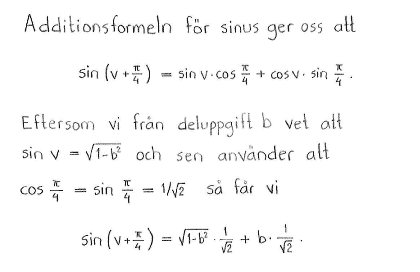4.3 Övningar
Sommarmatte 1
| Versionen från 30 april 2007 kl. 14.05 (redigera) Annagf (Diskussion | bidrag) (→Övning 4.3:7) ← Gå till föregående ändring |
Versionen från 30 april 2007 kl. 14.06 (redigera) (ogör) Annagf (Diskussion | bidrag) (→Övning 4.3:8) Gå till nästa ändring → |
||
| Rad 453: | Rad 453: | ||
| <div class=NavContent> | <div class=NavContent> | ||
| Lösning till delfråga b<br />[[Bild:4_3_8b.gif]] | Lösning till delfråga b<br />[[Bild:4_3_8b.gif]] | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | ==Övning 4.3:9== | ||
| + | <div class="ovning"> | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <div class=NavFrame style="CLEAR: both"> | ||
| + | <div class=NavHead>Facit </div> | ||
| + | <div class=NavContent> | ||
| + | Facit till alla delfrågorna<br \> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | <div class=NavFrame style="CLEAR: both"> | ||
| + | <div class=NavHead>Lösning a </div> | ||
| + | <div class=NavContent> | ||
| + | Lösning till delfråga a<br />[[Bild:4_3_9a.gif]] | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | <div class=NavFrame style="CLEAR: both"> | ||
| + | <div class=NavHead>Lösning b </div> | ||
| + | <div class=NavContent> | ||
| + | Lösning till delfråga b<br />[[Bild:4_3_9b.gif]] | ||
| </div> | </div> | ||
| </div> | </div> | ||
Versionen från 30 april 2007 kl. 14.06
Innehåll |
Övning 4.3:1
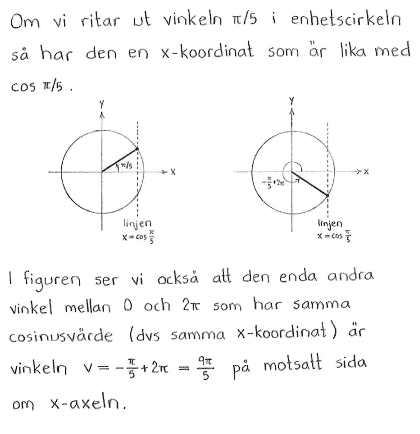
Bestäm de vinklar $v$ mellan $\displaystyle \frac{\pi}{2}$ och $2\pi$ som uppfyller
| $\textrm{a) }$ | $\cos{v}=\cos{\displaystyle \frac{\pi}{5}}$ | $\textrm{b) }$ | $\sin{v}=\sin{\displaystyle \frac{\pi}{7}}$ | $\textrm{c) }$ | $\tan{v}=\tan{\displaystyle \frac{2\pi}{7}}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $v = \displaystyle \frac{9\pi}{5}$ | $\textrm{b) }$ | $v = \displaystyle \frac{6\pi}{7}$ | $\textrm{c) }$ | $v = \displaystyle \frac{9\pi}{7}$ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Övning 4.3:2
Bestäm de vinklar $v$ mellan 0 och $\pi$ som uppfyller
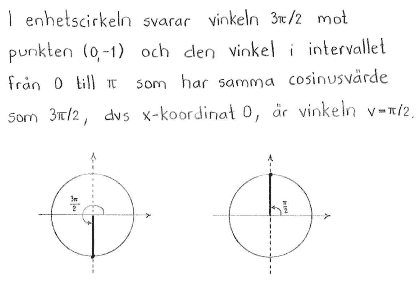
| $\textrm{a) }$ | $\cos{v} = \cos{\displaystyle \frac{3\pi}{2}}$ | $\textrm{b) }$ | $\cos{v} = \cos{ \displaystyle \frac{7\pi}{5}}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $v=\displaystyle \frac{\pi}{2}$ | $\textrm{b) }$ | $v=\displaystyle \frac{3\pi}{5}$ |
Lösning till delfråga a
Lösning till delfråga b
Övning 4.3:3
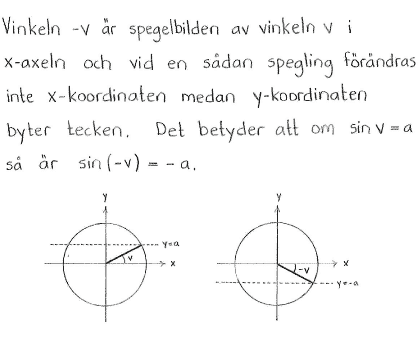
Antag att $-\displaystyle \frac{\pi}{2} \leq v \leq \displaystyle \frac{\pi}{2}$ och att $\sin{v} = a$. Uttryck med hjälp av $a$
| $\textrm{a) }$ | $\sin{(-v)}$ | $\textrm{b) }$ | $\sin{(\pi-v)}$ | $\textrm{c) }$ | $\cos{v}$ |
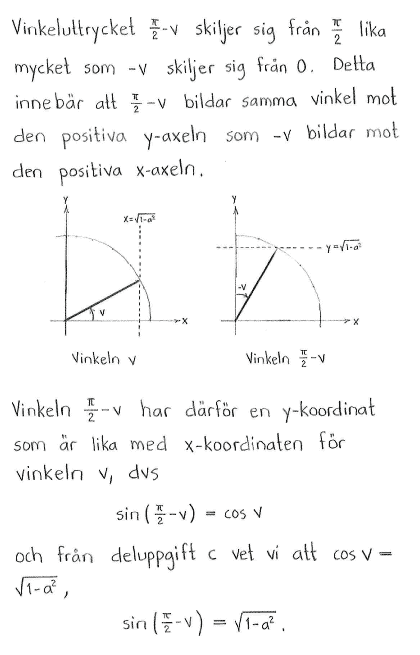
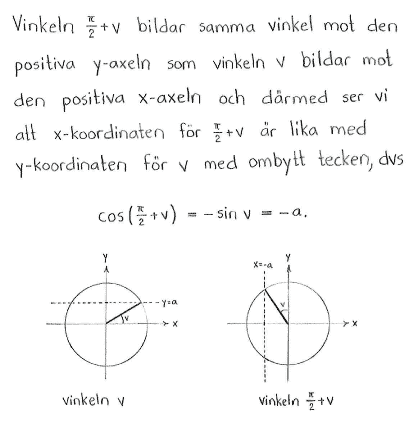
| $\textrm{d) }$ | $\sin{\left(\displaystyle \frac{\pi}{2}-v\right)}$ | $\textrm{e) }$ | $\cos{\left( \displaystyle \frac{\pi}{2} + v\right)}$ | $\textrm{f) }$ | $\sin{\left( \displaystyle \frac{\pi}{3} + v \right)}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $-a$ | $\textrm{b) }$ | $a$ | $\textrm{c) }$ | $\sqrt{1-a^2}$ |
| $\textrm{d) }$ | $\sqrt{1-a^2}$ | $\textrm{e) }$ | $-a$ | $\textrm{f) }$ | $\displaystyle \frac{\sqrt{3}}{2}\sqrt{1-a^2}+\displaystyle \frac{1}{2}\cdot a $ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
Lösning till delfråga e
Lösning till delfråga f
Övning 4.3:4
Antag att $0 \leq v \leq \pi$ och att $\cos{v}=b$. Uttryck med hjälp av $b$
| $\textrm{a) }$ | $\sin^2{v}$ | $\textrm{b) }$ | $\sin{v}$ | $\textrm{c) }$ | $\sin{2v}$ |
| $\textrm{d) }$ | $\cos{2v}$ | $\textrm{e) }$ | $\sin{\left( v+\displaystyle \frac{\pi}{4} \right)}$ | $\textrm{f) }$ | $\cos{\left( v-\displaystyle \frac{\pi}{3} \right)}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $1-b^2$ | $\textrm{b) }$ | $\sqrt{1-b^2}$ | $\textrm{c) }$ | $2b\sqrt{1-b^2}$ |
| $\textrm{d) }$ | $2b^2-1$ | $\textrm{e) }$ | $\sqrt{1-b^2}\cdot\displaystyle \frac{1}{\sqrt{2}} + b\cdot \displaystyle \frac{1}{\sqrt{2}} $ | $\textrm{f) }$ | $b\cdot\displaystyle \frac{1}{2}+\sqrt{1-b^2}\cdot\displaystyle \frac{\sqrt{3}}{2}$ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
Lösning till delfråga e
Lösning till delfråga f
Övning 4.3:5
För en spetsig vinkel $v$ i en triangel gäller att $\sin{v}=\displaystyle \frac{5}{7}$. Bestäm $\cos{v}$ och $\tan{v}$.
| $\cos{v}=\displaystyle \frac{2\sqrt{6}}{7}$ | $\tan{v}=\displaystyle \frac{5}{2\sqrt{6}}$ |
Övning 4.3:6
| $\textrm{a) }$ | Bestäm $\sin{v}$ och $\tan{v}$ om $\cos{v}=\displaystyle \frac{3}{4}$ och $\displaystyle \frac{3\pi}{2} \leq v \leq 2\pi$. |
| $\textrm{b) }$ | Bestäm $\cos{v}$ och $\tan{v}$ om $\sin{v}=\displaystyle \frac{3}{10}$ och $v$ ligger i den andra kvadranten. |
| $\textrm{c) }$ | Bestäm $\sin{v}$ och $\cos{v}$ om $\tan{v}=3$ och $\pi \leq v \leq \displaystyle \frac{3\pi}{2}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $\sin{v}=-\displaystyle \frac{\sqrt{7}}{4}$ och $\tan{v}=-\displaystyle \frac{\sqrt{7}}{3}$ |
| $\textrm{b) }$ | $\cos{v}=-\displaystyle \frac{\sqrt{91}}{10}$ och $\tan{v}=-\displaystyle \frac{3}{\sqrt{91}}$ |
| $\textrm{c) }$ | $\sin{v}=-\displaystyle \frac{3}{\sqrt{10}}$ och $\cos{v}=-\displaystyle \frac{1}{\sqrt{10}}$ |
Lösning till delfråga a
Bild:4 3 6a.gif
Lösning till delfråga b
Bild:4 3 6b.gif
Lösning till delfråga c
Bild:4 3 6c.gif
Övning 4.3:7
Bestäm $\sin{(x+y)}$ om
| $\textrm{a) }$ | $\sin{x}=\displaystyle \frac{2}{3}, \sin{y}=\displaystyle \frac{1}{3}$ och $x,y$ är vinklar i första kvadranten. |
| $\textrm{b) }$ | $\cos{x}=\displaystyle \frac{2}{5}, \cos{y}=\displaystyle \frac{3}{5}$ och $x,y$ är vinklar i första kvadranten. |
Facit till alla delfrågorna
| $\textrm{a) }$ | $\sin{(x+y)}=\displaystyle \frac{4\sqrt{2}+\sqrt{5}}{9}$ |
| $\textrm{b) }$ | $\sin{(x+y)}=\displaystyle \frac{3\sqrt{21}+8}{25}$ |
Lösning till delfråga a
Lösning till delfråga b
Övning 4.3:8
Facit till alla delfrågorna
Lösning till delfråga a
Lösning till delfråga b
Övning 4.3:9
Facit till alla delfrågorna
Lösning till delfråga a
Bild:4 3 9a.gif
Lösning till delfråga b
Bild:4 3 9b.gif
