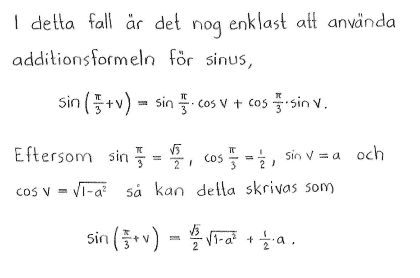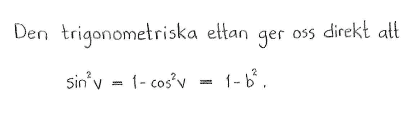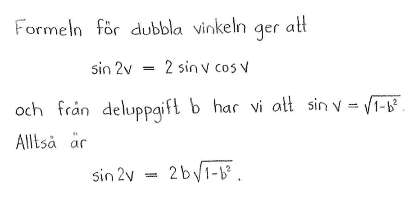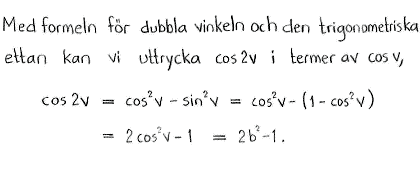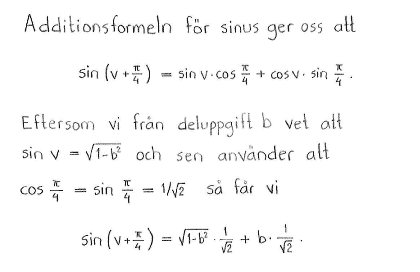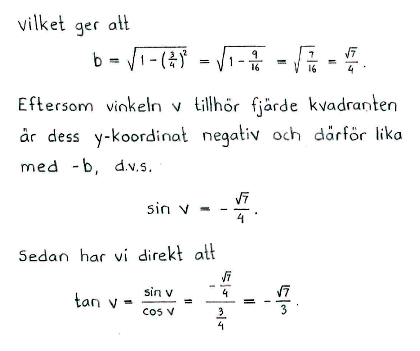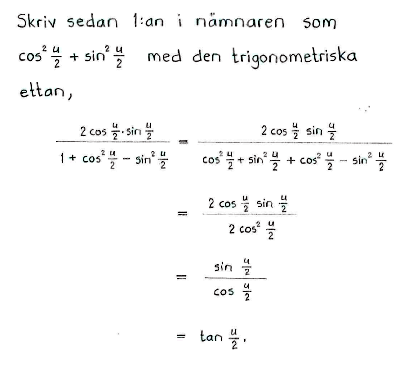4.3 Övningar
Sommarmatte 1
| Versionen från 15 maj 2007 kl. 13.04 (redigera) Tek (Diskussion | bidrag) (En del ändringar) ← Gå till föregående ändring |
Versionen från 23 maj 2007 kl. 12.05 (redigera) (ogör) Lina (Diskussion | bidrag) (→Övning 4.3:8) Gå till nästa ändring → |
||
| Rad 624: | Rad 624: | ||
| <td class="ntext>c)</td> | <td class="ntext>c)</td> | ||
| <td class="ntext width="100%">$\tan\displaystyle\frac{u}{2}=\frac{\sin u}{1+\cos u}$</td> | <td class="ntext width="100%">$\tan\displaystyle\frac{u}{2}=\frac{\sin u}{1+\cos u}$</td> | ||
| + | </tr> | ||
| + | <tr align="left"> | ||
| + | <td class="ntext>d)</td> | ||
| + | <td class="ntext width="100%">$\displaystyle\frac{\cos (u+v)}{\cos u \cos v}= 1- \tan u \tan v$</td> | ||
| </tr> | </tr> | ||
| </table> | </table> | ||
| Rad 669: | Rad 673: | ||
| <td align="center"> | <td align="center"> | ||
| [[Bild:4_3_8c-2(2).gif]] | [[Bild:4_3_8c-2(2).gif]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | <div class=NavFrame style="CLEAR: both"> | ||
| + | <div class=NavHead>Lösning d) </div> | ||
| + | <div class=NavContent> | ||
| + | Lösning till delfråga a) | ||
| + | <table width="100%"> | ||
| + | <tr> | ||
| + | <td align="center"> | ||
| + | [[Bild:4_3_8d.gif]] | ||
| </td> | </td> | ||
| </tr> | </tr> | ||
Versionen från 23 maj 2007 kl. 12.05
Övning 4.3:1
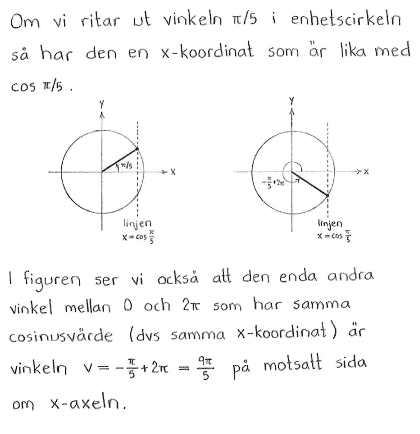
Bestäm de vinklar $\,v\,$ mellan $\,\displaystyle \frac{\pi}{2}\,$ och $\,2\pi\,$ som uppfyller
| a) | $\cos{v}=\cos{\displaystyle \frac{\pi}{5}}$ | b) | $\sin{v}=\sin{\displaystyle \frac{\pi}{7}}$ | c) | $\tan{v}=\tan{\displaystyle \frac{2\pi}{7}}$ |
Facit till alla delfrågor
| a) | $v = \displaystyle \frac{9\pi}{5}$ | b) | $v = \displaystyle \frac{6\pi}{7}$ | c) | $v = \displaystyle \frac{9\pi}{7}$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Övning 4.3:2
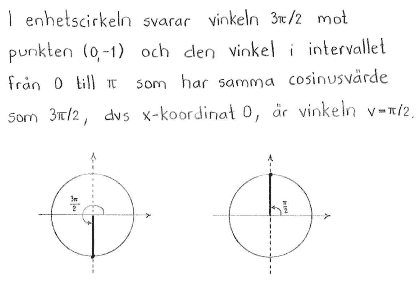
Bestäm de vinklar $\,v\,$ mellan 0 och $\,\pi\,$ som uppfyller
| a) | $\cos{v} = \cos{\displaystyle \frac{3\pi}{2}}$ | b) | $\cos{v} = \cos{ \displaystyle \frac{7\pi}{5}}$ |
Facit till alla delfrågor
| a) | $v=\displaystyle \frac{\pi}{2}$ | b) | $v=\displaystyle \frac{3\pi}{5}$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Övning 4.3:3
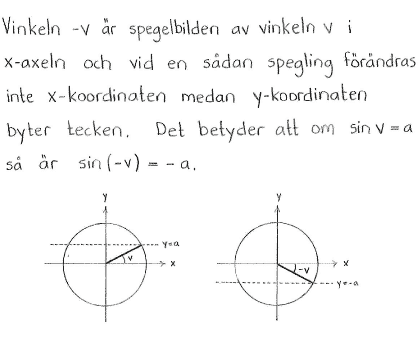
Antag att $\,-\displaystyle \frac{\pi}{2} \leq v \leq \displaystyle \frac{\pi}{2}\,$ och att $\,\sin{v} = a\,$. Uttryck med hjälp av $\,a$
| a) | $\sin{(-v)}$ | b) | $\sin{(\pi-v)}$ |
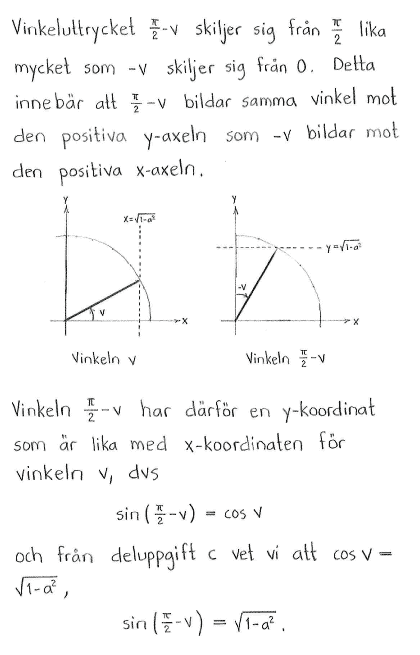
| c) | $\cos{v}$ | d) | $\sin{\left(\displaystyle \frac{\pi}{2}-v\right)}$ |
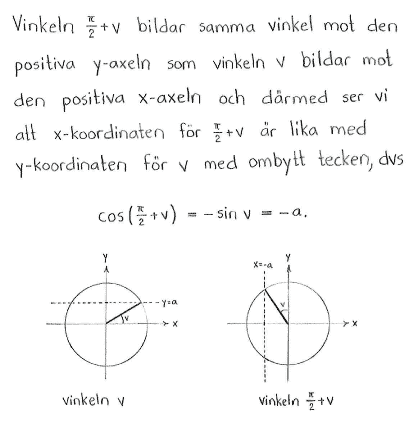
| e) | $\cos{\left( \displaystyle \frac{\pi}{2} + v\right)}$ | f) | $\sin{\left( \displaystyle \frac{\pi}{3} + v \right)}$ |
Facit till alla delfrågor
| a) | $-a$ | b) | $a$ |
| c) | $\sqrt{1-a^2}$ | d) | $\sqrt{1-a^2}$ |
| e) | $-a$ | f) | $\displaystyle \frac{\sqrt{3}}{2}\sqrt{1-a^2}+\displaystyle \frac{1}{2}\cdot a $ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
Övning 4.3:4
Antag att $\,0 \leq v \leq \pi\,$ och att $\,\cos{v}=b\,$. Uttryck med hjälp av $\,b\,$
| a) | $\sin^2{v}$ | b) | $\sin{v}$ |
| c) | $\sin{2v}$ | d) | $\cos{2v}$ |
| e) | $\sin{\left( v+\displaystyle \frac{\pi}{4} \right)}$ | f) | $\cos{\left( v-\displaystyle \frac{\pi}{3} \right)}$ |
Facit till alla delfrågor
| a) | $1-b^2$ | b) | $\sqrt{1-b^2}$ |
| c) | $2b\sqrt{1-b^2}$ | d) | $2b^2-1$ |
| e) | $\sqrt{1-b^2}\cdot\displaystyle \frac{1}{\sqrt{2}} + b\cdot \displaystyle \frac{1}{\sqrt{2}} $ | f) | $b\cdot\displaystyle \frac{1}{2}+\sqrt{1-b^2}\cdot\displaystyle \frac{\sqrt{3}}{2}$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
Övning 4.3:5
För en spetsig vinkel $\,v\,$ i en triangel gäller att $\,\sin{v}=\displaystyle \frac{5}{7}\,$. Bestäm $\,\cos{v}\,$ och $\,\tan{v}\,$.
| $\cos{v}=\displaystyle \frac{2\sqrt{6}}{7}\quad$ och $\quad\tan{v}=\displaystyle \frac{5}{2\sqrt{6}}\,$. |
|
|
|
|
Övning 4.3:6
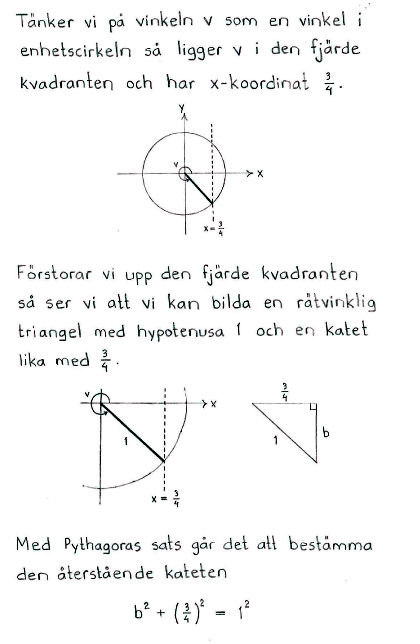
| a) | Bestäm $\ \sin{v}\ $ och $\ \tan{v}\ $ om $\ \cos{v}=\displaystyle \frac{3}{4}\ $ och $\ \displaystyle \frac{3\pi}{2} \leq v \leq 2\pi\,$. |
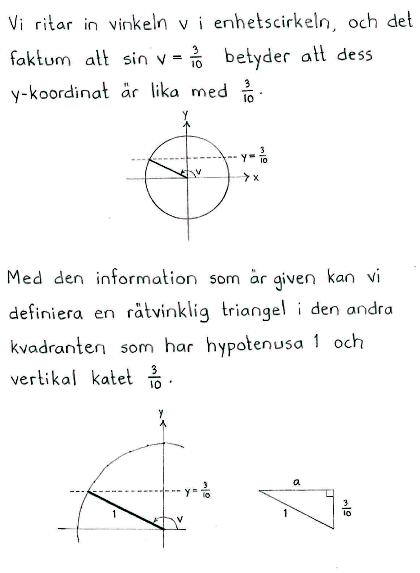
| b) | Bestäm $\ \cos{v}\ $ och $\ \tan{v}\ $ om $\ \sin{v}=\displaystyle \frac{3}{10}\ $ och $\,v\,$ ligger i den andra kvadranten. |
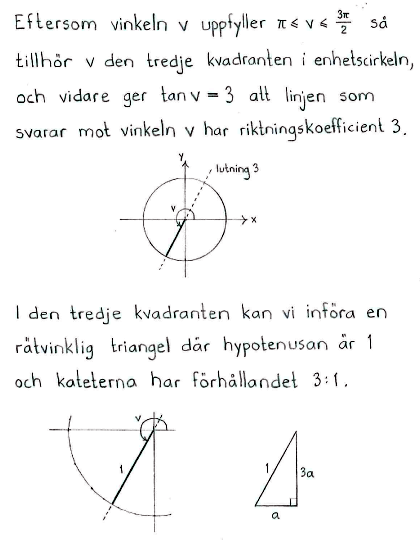
| c) | Bestäm $\ \sin{v}\ $ och $\ \cos{v}\ $ om $\ \tan{v}=3\ $ och $\ \pi \leq v \leq \displaystyle \frac{3\pi}{2}\,$. |
Facit till alla delfrågor
| a) | $\sin{v}=-\displaystyle \frac{\sqrt{7}}{4}\quad$ och $\quad\tan{v}=-\displaystyle \frac{\sqrt{7}}{3}\,$. |
| b) | $\cos{v}=-\displaystyle \frac{\sqrt{91}}{10}\quad$ och $\quad\tan{v}=-\displaystyle \frac{3}{\sqrt{91}}\,$. |
| c) | $\sin{v}=-\displaystyle \frac{3}{\sqrt{10}}\quad$ och $\quad\cos{v}=-\displaystyle \frac{1}{\sqrt{10}}\,$. |
Lösning till delfråga a)
|
|
|
|
Lösning till delfråga b)
|
|
|
|
Lösning till delfråga c)
|
|
|
|
Övning 4.3:7
Bestäm $\ \sin{(x+y)}\ $ om
| a) | $\sin{x}=\displaystyle \frac{2}{3}\,$, $\ \sin{y}=\displaystyle \frac{1}{3}\ $ och $\,x\,$, $\,y\,$ är vinklar i första kvadranten. |
| b) | $\cos{x}=\displaystyle \frac{2}{5}\,$, $\ \cos{y}=\displaystyle \frac{3}{5}\ $ och $\,x\,$, $\,y\,$ är vinklar i första kvadranten. |
Facit till alla delfrågor
| a) | $\sin{(x+y)}=\displaystyle \frac{4\sqrt{2}+\sqrt{5}}{9}$ |
| b) | $\sin{(x+y)}=\displaystyle \frac{3\sqrt{21}+8}{25}$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Övning 4.3:8
Visa följande trigonometriska samband
| a) | $\tan^2v=\displaystyle\frac{\sin^2v}{1-\sin^2v}$ |
| b) | $\displaystyle \frac{1}{\cos v}-\tan v=\frac{\cos v}{1+\sin v}$ |
| c) | $\tan\displaystyle\frac{u}{2}=\frac{\sin u}{1+\cos u}$ |
| d) | $\displaystyle\frac{\cos (u+v)}{\cos u \cos v}= 1- \tan u \tan v$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
|
|
Lösning till delfråga a)
|
|
Övning 4.3:9
|
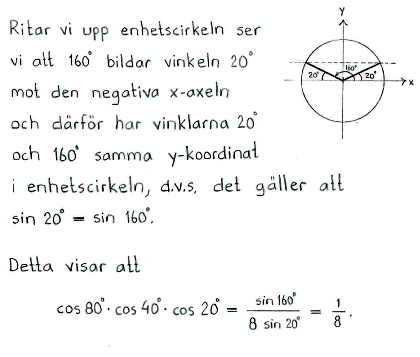
Visa "Feynmans likhet" $$\cos 20^\circ \cdot \cos 40^\circ \cdot \cos 80^\circ = \displaystyle\frac{1}{8}\,\mbox{.}$$ (Ledtråd: Använd formeln för dubbla vinkeln på $\,\sin 160^\circ\,$.) |
|
|
|
|
