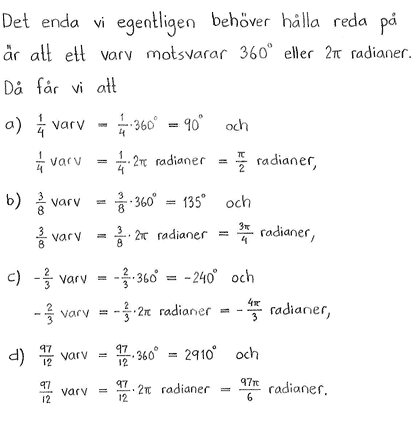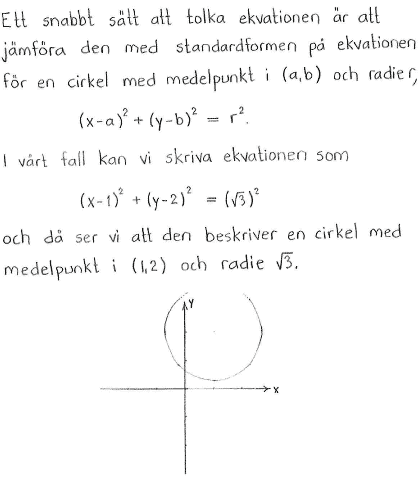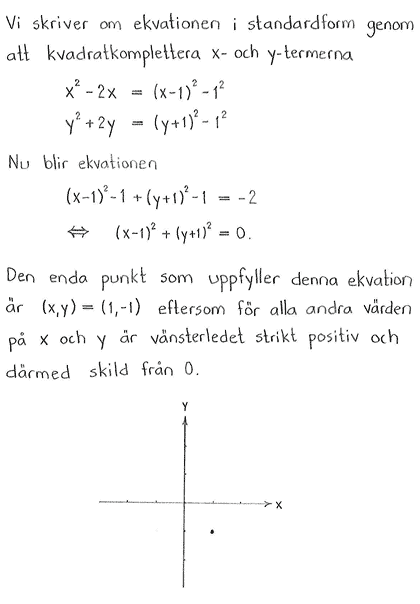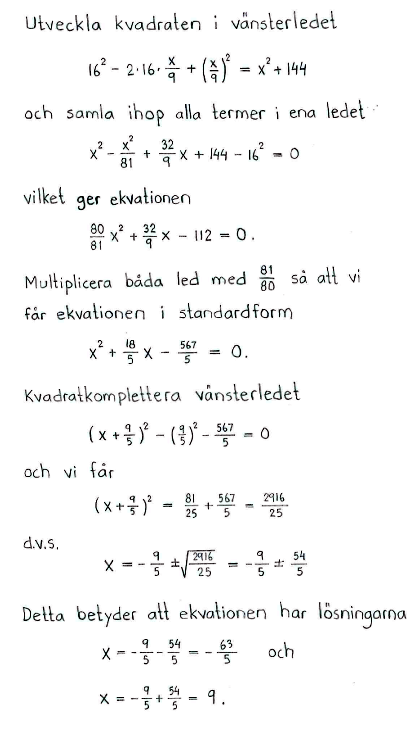4.1 Övningar
Sommarmatte 1
| Versionen från 31 maj 2007 kl. 07.04 (redigera) KTH.SE:u1rp004j (Diskussion | bidrag) ← Gå till föregående ändring |
Versionen från 25 juni 2007 kl. 11.00 (redigera) (ogör) KTH.SE:u1m1gion (Diskussion | bidrag) (→Övning 4.1:6 - lade till facit (Johan T)) Gå till nästa ändring → |
||
| Rad 1: | Rad 1: | ||
| - | |||
| ==Övning 4.1:1== | ==Övning 4.1:1== | ||
| <div class="ovning"> | <div class="ovning"> | ||
| Rad 362: | Rad 361: | ||
| <tr align="left"> | <tr align="left"> | ||
| <td class="ntext">a)</td> | <td class="ntext">a)</td> | ||
| - | <td class="ntext" width="50%">BILD</td> | + | <td class="ntext" width="50%">En cirkel med radie 3 och medelpunkt i origo.</td> |
| <td class="ntext">b)</td> | <td class="ntext">b)</td> | ||
| - | <td class="ntext" width="50%">BILD</td> | + | <td class="ntext" width="50%">En cirkel med radie $\sqrt 3$ och medelpunkt i punkten (1, 2).</td> |
| </tr> | </tr> | ||
| <tr align="left"> | <tr align="left"> | ||
| <td class="ntext">c)</td> | <td class="ntext">c)</td> | ||
| - | <td class="ntext" width="50%">BILD</td> | + | <td class="ntext" width="50%">En cirkel med radie $\frac{1}{3}\sqrt 10$ och medelpunkt i punkten (1/3, -7/3).</td> |
| </tr> | </tr> | ||
| <tr><td height="5px"/></tr> | <tr><td height="5px"/></tr> | ||
Versionen från 25 juni 2007 kl. 11.00
Innehåll |
Övning 4.1:1
Skriv i grader och radianer
| a) | $\displaystyle \frac{1}{4} \textrm{ varv} $ | b) | $\displaystyle \frac{3}{8} \textrm{ varv}$ |
| c) | $-\displaystyle \frac{2}{3}\textrm{ varv}$ | d) | $\displaystyle \frac{97}{12} \textrm{ varv} $ |
Facit till alla delfrågor
| a) | $90^\circ\ $ och $\ \displaystyle \frac{\pi}{2} \textrm{ rad} $ | b) | $135^\circ\ $ och $\ \displaystyle \frac{3\pi}{4} \textrm{ rad}$ |
| c) | $-240^\circ\ $ och $\ \displaystyle -\frac{4\pi}{3} \textrm{ rad}$ | d) | $2910^\circ\ $ och $\ \displaystyle \frac{97\pi}{6} \textrm{ rad}$ |
|
|
Övning 4.1:2
Omvandla till radianer
| a) | $45^\circ$ | b) | $135^\circ$ | c) | $-63^\circ$ | d) | $270^\circ$ |
Facit till alla delfrågor
| a) | $\displaystyle \frac{\pi}{4}\textrm{ rad}$ | b) | $\displaystyle \frac{3\pi}{4}\textrm{ rad}$ | c) | $-\displaystyle \frac{7\pi}{20}\textrm{ rad}$ | d) | $\displaystyle \frac{3\pi}{2}\textrm{ rad}$ |
|
|
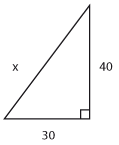
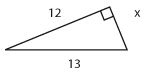
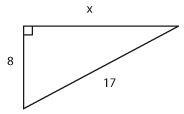
Övning 4.1:3
Bestäm längden av sidan som är markerad med $\,x$
| a) |  |
b) |  |
c) |  |
Facit till alla delfrågor
| a) | $x=50$ | b) | $x=5$ | c) | $x=15$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Övning 4.1:4
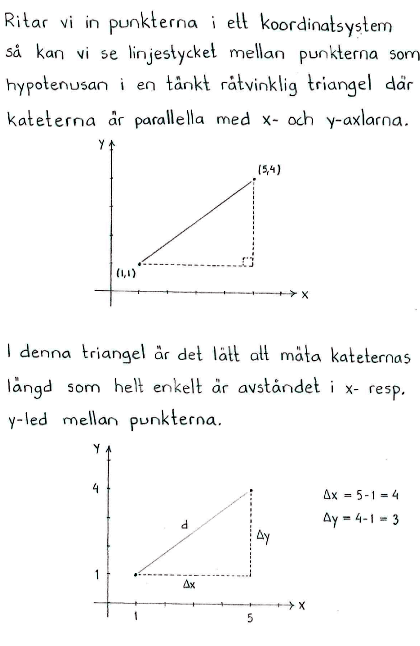
| a) | Bestäm avståndet mellan punkterna (1,1) och (5,4). |
| b) | Bestäm avståndet mellan punkterna (-2,5) och (3,-1). |
| c) | Hitta den punkt på x-axeln som ligger lika långt från punkterna (3,3) och (5,1). |
Facit till alla delfrågor
| a) | $5 \textrm{ l.e.}$ |
| b) | $\sqrt{61} \textrm{ l.e.}$ |
| c) | $(2,0)$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
|
|
Övning 4.1:5
| a) | Bestäm ekvationen för en cirkel med medelpunkt i (1,2) och radie 2. |
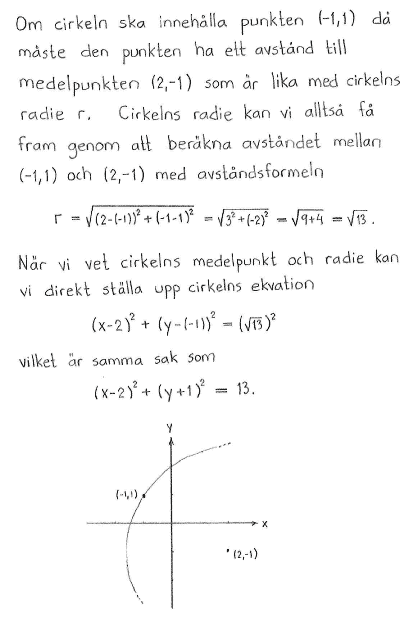
| b) | Bestäm ekvationen för den cirkel som har medelpunkt i (2,-1) och innehåller punkten (-1,1). |
Facit till alla delfrågor
| a) | $(x-1)^2+(y-2)^2=4$ |
| b) | $(x-2)^2+(y+1)^2=13$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
|
|
Övning 4.1:6
Skissera följande cirklar
| a) | $x^2+y^2=9$ | b) | $(x-1)^2+(y-2)^2=3$ |
| c) | $(3x-1)^2+(3y+7)^2=10$ | ||
Facit till alla delfrågor
| a) | En cirkel med radie 3 och medelpunkt i origo. | b) | En cirkel med radie $\sqrt 3$ och medelpunkt i punkten (1, 2). |
| c) | En cirkel med radie $\frac{1}{3}\sqrt 10$ och medelpunkt i punkten (1/3, -7/3). | ||
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
|
|
Övning 4.1:7
Skissera följande cirklar
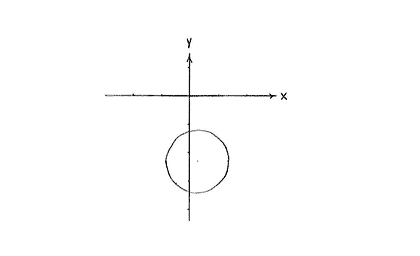
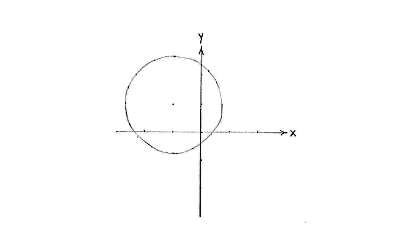
| a) | $x^2+2x+y^2-2y=1$ | b) | $x^2+y^2+4y=0$ |
| c) | $x^2-2x+y^2+6y=-3$ | d) | $x^2-2x+y^2+2y=-2$ |
Facit till alla delfrågor
| a) | BILD | b) | BILD |
| c) | BILD | d) | BILD |
Lösning till delfråga a)
|
|
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Övning 4.1:8
Hur många varv snurrar ett hjul med radie 50 cm när det rullar 10m?
| $\displaystyle \frac{10}{\pi}\textrm{ varv }\approx 3,2 \textrm{ varv} $ |
|
|
Övning 4.1:9
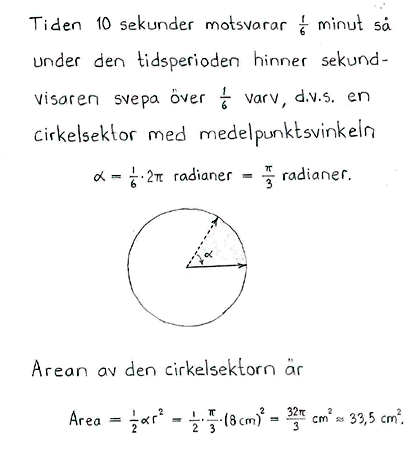
På en klocka är sekundvisaren 8 cm lång. Hur stor area sveper den över på 10 sekunder?
| $\displaystyle \frac{32\pi}{3} \textrm{ cm}^2 \approx 33,5 \textrm{ cm}^2$ |
|
|
Övning 4.1:10
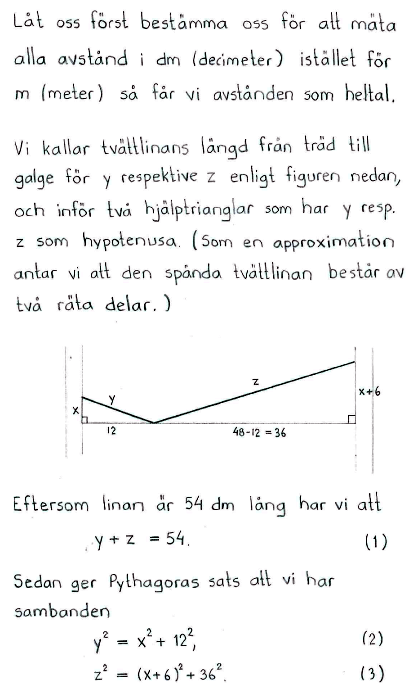
En 5,4 m lång tvättlina hänger mellan två vertikala träd på 4,8 m avstånd från varandra. Linans ena ände är fäst 0,6 m högre än den andra änden, och 1,2 m från trädet där linan har sin lägre infästning hänger en kavaj på en galge. Bestäm hur mycket under den nedre infästningspunkten som galgen hänger (dvs. avståndet $\,x\,$ i figuren).
| BILD |
| $x=9$ dm |
|
|
|
|
|
|
|
|
|
|
