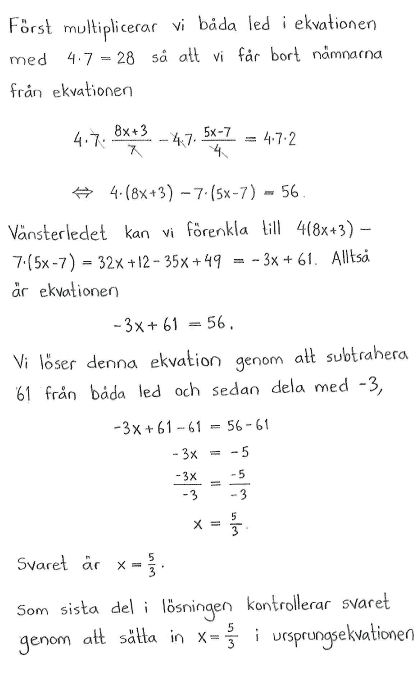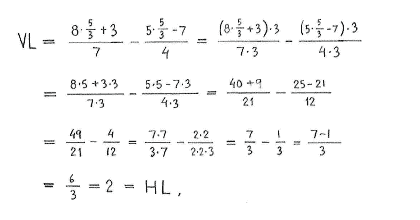2.2 Övningar
Sommarmatte 1
(Skillnad mellan versioner)
| Versionen från 28 april 2007 kl. 15.28 (redigera) Annagf (Diskussion | bidrag) (→Övning 2.2:3) ← Gå till föregående ändring |
Versionen från 28 april 2007 kl. 15.29 (redigera) (ogör) Annagf (Diskussion | bidrag) (→Övning 2.2:3) Gå till nästa ändring → |
||
| Rad 161: | Rad 161: | ||
| <tr align="left"> | <tr align="left"> | ||
| <td class="ntext">c) </td> | <td class="ntext">c) </td> | ||
| - | <td class="ntext">$(\frac{1}{x-1}-\frac{1}{x+1})(x^2+\frac{1}{2}=\frac{6x-1}{3x-3}$</td> | + | <td class="ntext">$(\frac{1}{x-1}-\frac{1}{x+1})(x^2+\frac{1}{2})=\frac{6x-1}{3x-3}$</td> |
| <td class="ntext">d) </td> | <td class="ntext">d) </td> | ||
| <td class="ntext">$(x^2+4x+1)^2+3x^4-2x^2=(2x^2+2x+3)^2$</td> | <td class="ntext">$(x^2+4x+1)^2+3x^4-2x^2=(2x^2+2x+3)^2$</td> | ||
Versionen från 28 april 2007 kl. 15.29
Övning 2.2:1
Lös ekvationerna
| a) | $x-2=-1$ | b) | $2x+1=13$ |
| c) | $\frac{1}{3}x-1=x$ | d) | $5x+7=2x-6$ |
Facit
Facit till alla delfrågorna
| a) | $x=1$ | b) | $x=6$ |
| c) | $x=-\frac{3}{2}$ | d) | $x=-\frac{13}{3}$ |
Lösning a
Lösning till delfråga a 
Lösning b
Lösning till delfråga b 
Lösning c
Lösning till delfråga c 
Lösning d
Lösning till delfråga d 
Övning 2.2:2
Lös ekvationerna
| a) | $\displaystyle\frac{5x}{6}-\displaystyle\frac{x+2}{9}=\displaystyle\frac{1}{2}$ | b) | $\displaystyle\frac{8x+3}{7}-\displaystyle\frac{5x-7}{4}=2$ |
| c) | $(x+3)^2-(x-5)^2=6x+4$ | d) | $(x^2+4x+1)^2+3x^4-2x^2=(2x^2+2x+3)^2$ |
Facit
Facit till alla delfrågorna
| a) | $x=1$ | b) | $x=\displaystyle\frac{5}{3}$ |
| c) | $x=2$ | d) | $x=-2$ |
Lösning a
Lösning till delfråga a 
Lösning b
Lösning till delfråga b 
Lösning c
Lösning till delfråga c 
Lösning d
Lösning till delfråga d 
Övning 2.2:3
Lös ekvationerna
| a) | $\displaystyle\frac{x+3}{x-3}-\displaystyle\frac{x+5}{x-2}=0$ | b) | $\displaystyle\frac{4x}{4x-7}-\displaystyle\frac{1}{2x-3}=1$ |
| c) | $(\frac{1}{x-1}-\frac{1}{x+1})(x^2+\frac{1}{2})=\frac{6x-1}{3x-3}$ | d) | $(x^2+4x+1)^2+3x^4-2x^2=(2x^2+2x+3)^2$ |
Facit
Facit till alla delfrågorna
| a) | $x=9$ | b) | $x=\displaystyle\frac{7}{5}$ |
| c) | $x=2$ | d) | $x=-2$ |
Lösning a
Lösning till delfråga a 
Lösning b
Lösning till delfråga b
Bild:2 2 3b.gif
Lösning c
Lösning till delfråga c
Bild:2 2 3c.gif
Lösning d
Lösning till delfråga d
Bild:2 2 3d.gif
