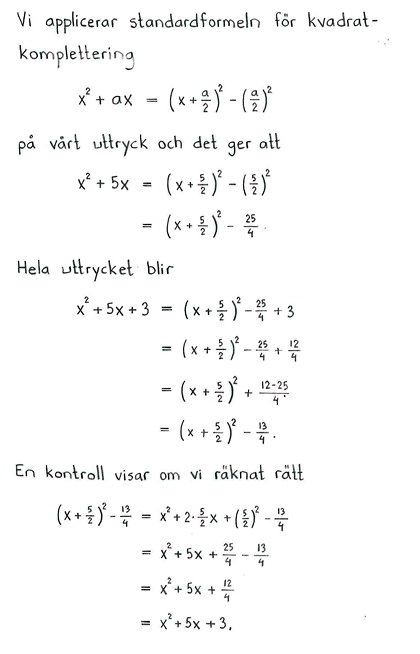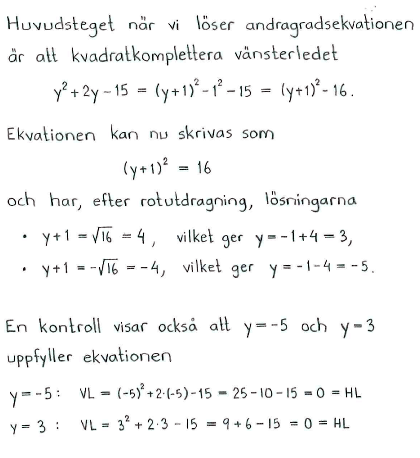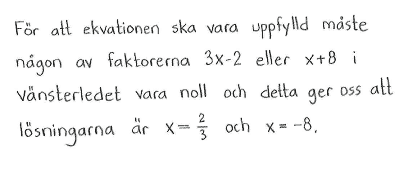2.3 Övningar
Sommarmatte 1
(Skillnad mellan versioner)
| Versionen från 28 april 2007 kl. 18.54 (redigera) Ossiang (Diskussion | bidrag) (→Ouml;vning 2.3:4) ← Gå till föregående ändring |
Versionen från 28 april 2007 kl. 18.55 (redigera) (ogör) Ossiang (Diskussion | bidrag) (→Övning 2.3:4) Gå till nästa ändring → |
||
| Rad 286: | Rad 286: | ||
| <div class=NavContent> | <div class=NavContent> | ||
| Facit till alla delfrågorna<br \> | Facit till alla delfrågorna<br \> | ||
| + | <table width="100%" cellspacing="10px"> | ||
| + | <tr><td height="5px"/></tr> | ||
| + | <tr align="left"> | ||
| + | <td class="ntext">a)</td> | ||
| + | <td class="ntext">$ax^2-ax-2a=0, a\ne 0$</td> | ||
| + | </tr> | ||
| + | <tr><td height="5px"/></tr> | ||
| + | <tr align="left"> | ||
| + | <td class="ntext">b)</td> | ||
| + | <td class="ntext">$ax^2-2ax-2a=0, a\ne 0$</td> | ||
| + | </tr> | ||
| + | <tr><td height="5px"/></tr> | ||
| + | <tr align="left"> | ||
| + | <td class="ntext">c)</td> | ||
| + | <td class="ntext">$ax^2-(3+\sqrt{3})ax+3\sqrt{3}a=0, a\ne 0$</td> | ||
| + | </tr> | ||
| + | <tr><td height="5px"/></tr> | ||
| + | </table> | ||
| </div> | </div> | ||
Versionen från 28 april 2007 kl. 18.55
Innehåll |
Övning 2.3:1
Kvadratkomplettera följande uttryck
| a) | $x^2-2x$ | b) | $x^2+2x-1$ | c) | $5+2x-x^2$ | d) | $x^2+5x+3$ |
Facit
Facit till alla delfrågorna
| a) | $(x-1)^2-1$ | b) | $(x+1)^2-2$ | c) | $-(x-1)^2+6$ | d) | $\left(x+\displaystyle \frac{5}{2}\right)^2-\displaystyle \frac{13}{4}$ |
Övning 2.3:2
Lös följande andragradsekvationer med kvadratkomplettering
| a) | $x^2-4x+3=0$ | b) | $y^2+2y-15=0$ | c) | $y^2+3y+4=0$ |
| d) | $4x^2-28x+13=0$ | e) | $5x^2+2x-3=0$ | f) | $3x^2-10x+8=0$ |
Facit
Facit till alla delfrågorna
| a) | $\left\{ \matrix{ x_1 = 1 \cr x_2 = 3 }\right. $ | b) | $ \left\{ \matrix{ y_1 = -5 \cr y_2 = 3 }\right. $ | c) | saknar lösning* |
| d) | $ \left\{ \matrix{ x_1 = \frac{1}{2} \cr x_2 = \frac{13}{2} }\right. $ | e) | $\left\{ \matrix{ x_1 = -1 \cr x_2 = \frac{3}{5} }\right. $ | f) | $ \left\{ \matrix{ x_1 = \frac{4}{3} \cr x_2 = 2 }\right. $ |
- ) ekvationen saknar reella lösningar
Övning 2.3:3
Lös följande ekvationer direkt
| a) | $x(x+3)=0$ | b) | $(x-3)(x+5)=0$ |
| c) | $5(3x-2)(x+8)=0$ | d) | $x(x+3)-x(2x-9)=0$ |
| e) | $(x+3)(x-1)-(x+3)(2x-9)=0$ | f) | $x(x^2-2x)+x(2-x)=0$ |
Facit
Facit till alla delfrågorna
| a) | $\left\{ \matrix { x_1 & = 0 \cr x_2 & = -3 }\right.$ | b) | $\left\{ \matrix { x_1 & = 3 \cr x_2 & = -5 }\right. $ |
| c) | $\left\{ \matrix { x_1 & = \frac{2}{3} \cr x_2 & = -8 }\right. $ | d) | $\left\{ \matrix { x_1 & = 0 \cr x_2 & = 12 }\right. $ |
| e) | $\left\{ \matrix { x_1 & = -3 \cr x_2 & = 8 }\right. $ | f) | $\left\{ \matrix { x_1 & = 0 \cr x_2 & = 1 \cr x_3 & = 2 }\right. $ |
Övning 2.3:4
Bestäm en andragradsekvation som har rötterna
| a) | $-1$ och $2$ | b) | $1+\sqrt{3}$ och $1-\sqrt{3}$ | c) | $3$ och $\sqrt{3}$ |
Facit
Facit till alla delfrågorna
| a) | $ax^2-ax-2a=0, a\ne 0$ |
| b) | $ax^2-2ax-2a=0, a\ne 0$ |
| c) | $ax^2-(3+\sqrt{3})ax+3\sqrt{3}a=0, a\ne 0$ |
Lösning
Lösning till delfråga
[[Bild:]]