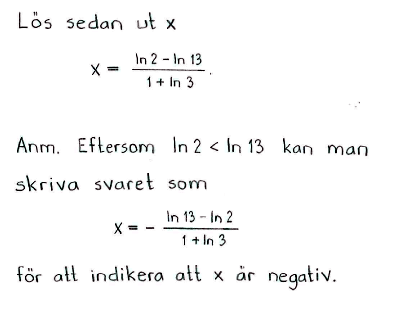3.4 Övningar
Sommarmatte 1
(Skillnad mellan versioner)
| Versionen från 29 april 2007 kl. 14.02 (redigera) Ossiang (Diskussion | bidrag) (→Övning 3.4:2) ← Gå till föregående ändring |
Versionen från 29 april 2007 kl. 14.08 (redigera) (ogör) Ossiang (Diskussion | bidrag) (→Övning 3.4:2) Gå till nästa ändring → |
||
| Rad 79: | Rad 79: | ||
| <tr align="left"> | <tr align="left"> | ||
| <td class="ntext">a)</td> | <td class="ntext">a)</td> | ||
| - | <td class="ntext">$x=$</td> | + | <td class="ntext">$ \left\{ \matrix{ x_1=\sqrt2 \cr x_2=-\sqrt2 } \right. $</td> |
| <td class="ntext">b)</td> | <td class="ntext">b)</td> | ||
| - | <td class="ntext">$x=$</td> | + | <td class="ntext">$x=\left(\displaystyle\frac{\sqrt17}{2}-\frac{1}{2}$</td> |
| <td class="ntext">c)</td> | <td class="ntext">c)</td> | ||
| - | <td class="ntext">$ \left\{ \matrix{ x_1=\sqrt2 \cr x_2=-\sqrt2 } \right. $</td> | + | <td class="ntext">$$</td> |
| </tr> | </tr> | ||
Versionen från 29 april 2007 kl. 14.08
Övning 3.4:1
Lös ekvationerna
| a) | $e^x=13$ | b) | $13e^x=2\cdot3^{-x}$ | c) | $3e^x=7\cdot2^x$ |
Facit
Facit till alla delfrågorna
| a) | $x=\ln 13$ | b) | $x=\displaystyle\frac{\ln 2 - \ln 13}{1+\ln 3}$ | c) | $x=\displaystyle\frac{\ln 7 - \ln 3}{1-\ln 2}$ |
Lösning a
Lösning till delfråga a
Lösning b
Lösning till delfråga b
Lösning
Lösning till delfråga 
Övning 3.4:2
Lös ekvationerna
| a) | $2^{\scriptstyle x^2-2}=1$ | b) | $e^{2x}+e^x=4$ | c) | $3e^{x^2}=2^x$ |
Facit
Facit till alla delfrågorna
| a) | $ \left\{ \matrix{ x_1=\sqrt2 \cr x_2=-\sqrt2 } \right. $ | b) | $x=\left(\displaystyle\frac{\sqrt17}{2}-\frac{1}{2}$ | c) | $$ |
Lösning
Lösning till delfråga
[[Bild:]]
