4.1 Vinklar och cirklar
Sommarmatte 1
| Versionen från 7 maj 2007 kl. 14.03 (redigera) Lina (Diskussion | bidrag) ← Gå till föregående ändring |
Versionen från 8 maj 2007 kl. 12.40 (redigera) (ogör) Tek (Diskussion | bidrag) (En del ändringar) Gå till nästa ändring → |
||
| Rad 1: | Rad 1: | ||
| + | __NOTOC__ | ||
| <table><tr><td width="600"> | <table><tr><td width="600"> | ||
| - | |||
| - | =4.1 Vinklar och cirklar= | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| Rad 11: | Rad 10: | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| - | '''Läromål:''' | + | '''Lärandemål:''' |
| Efter detta avsnitt ska du ha lärt dig att: | Efter detta avsnitt ska du ha lärt dig att: | ||
| - | *Omvandla mellan grader, radianer och varv | + | *Omvandla mellan grader, radianer och varv. |
| - | *Beräkna arean och omkretsen av en cirkelsektor | + | *Beräkna arean och omkretsen av en cirkelsektor. |
| - | *Beräkna avståndet mellan två punkter i planet | + | *Beräkna avståndet mellan två punkter i planet. |
| - | *Skissera cirklar med hjälp av att kvadratkomplettera deras ekvationer | + | *Skissera cirklar med hjälp av att kvadratkomplettera deras ekvationer. |
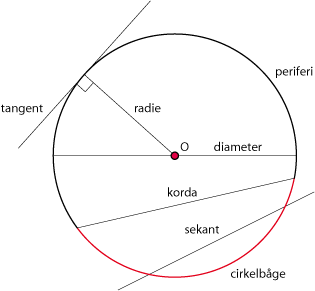
| *Använda begreppen enhetscirkel, tangent, radie, diameter, pereferi, korda och cirkelbåge. | *Använda begreppen enhetscirkel, tangent, radie, diameter, pereferi, korda och cirkelbåge. | ||
| - | *Lösa geometriska problem som innehåller cirklar | + | *Lösa geometriska problem som innehåller cirklar. |
| </div> | </div> | ||
| Rad 38: | Rad 37: | ||
| Det finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer. | Det finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer. | ||
| - | *'''Grader.''' Om ett helt varv delas in i 360 delar, så kallas varje del $1$ grad. Beteckningen för grader är $ ^\circ$. | + | *'''Grader.''' Om ett helt varv delas in i 360 delar, så kallas varje del 1 grad. Beteckningen för grader är $ ^\circ$. |
| Bild: figur 3.2.1 | Bild: figur 3.2.1 | ||
| - | *'''Radianer.''' Ett annat sätt att mäta vinklar är att omvända längden av vinkelns cirkelbåge i förhållandet till radien som mått på vinkeln. Detta vinkelmått kallas för radian. Ett varv är alltså $2\pi$ radianer eftersom cirkelns omkrets är $2\pi r$, där $r$ är cirkelns radie. | + | *'''Radianer.''' Ett annat sätt att mäta vinklar är att använda längden av vinkelns cirkelbåge i förhållande till radien som mått på vinkeln. Detta vinkelmått kallas för radian. Ett varv är alltså $\,2\pi\,$ radianer eftersom cirkelns omkrets är $\,2\pi r\,$, där $\,r\,$ är cirkelns radie. |
| Bild: figurer 3.2.2 och figurer 3.2.3 | Bild: figurer 3.2.2 och figurer 3.2.3 | ||
| - | Ett helt varv är $360^\circ$ eller $2\pi$ radianer och det gör att | + | Ett helt varv är $\,360^\circ\,$ eller $\,2\pi\,$ radianer och det gör att |
| - | $$1^\circ = \frac{1}{360} \cdot 2\pi \mbox{ radianer } = \frac{\pi}{180} \mbox{ radianer }$$ | + | $$\eqalign{&1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radianer } = \frac{\pi}{180}\ \mbox{ radianer,}\cr &1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ = \frac{180^\circ}{\pi}\,\mbox{.}}$$ |
| - | $$1 \mbox{ radianer } = \frac{1}{2\pi} \cdot 360^\circ = \frac{180^\circ}{\pi}$$ | + | |
| Dessa omvandlingsfaktorer kan användas för att konvertera mellan grader och radianer. | Dessa omvandlingsfaktorer kan användas för att konvertera mellan grader och radianer. | ||
| Rad 56: | Rad 54: | ||
| <ol type="a"> | <ol type="a"> | ||
| - | <li>$30^\circ = 30 \cdot 1^\circ = 30 \cdot \displaystyle \frac{\pi}{180} \mbox{ radianer } = \displaystyle \frac{\pi}{6} \mbox{ radianer }$ <br><br> | + | <li>$30^\circ = 30 \cdot 1^\circ = 30 \cdot \displaystyle \frac{\pi}{180}\ \mbox{ radianer } = \displaystyle \frac{\pi}{6}\ \mbox{ radianer }$ <br><br> |
| - | <li>$ \displaystyle \frac{\pi}{8} \mbox {radianer } = \displaystyle \frac{\pi}{8} \cdot (1 \; \mbox{radian }) = \displaystyle \frac{\pi}{8} \cdot \displaystyle \frac{180^\circ}{\pi} = 22,5^\circ$ | + | <li>$ \displaystyle \frac{\pi}{8}\ \mbox { radianer } = \displaystyle \frac{\pi}{8} \cdot (1 \; \mbox{radian}\,) = \displaystyle \frac{\pi}{8} \cdot \displaystyle \frac{180^\circ}{\pi} = 22{,}5^\circ$ |
| </ol> | </ol> | ||
| </div> | </div> | ||
| - | I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än $360^\circ$. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv. | + | I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än 360°. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv. |
| Bild: Figur 3.2.4 | Bild: Figur 3.2.4 | ||
| Rad 70: | Rad 68: | ||
| <ol type="a"> | <ol type="a"> | ||
| - | <li>Vinklar $-55^\circ$ och $665^\circ$ anger samma riktning eftersom $$-55^\circ + 2 \cdot 360^\circ = 665^\circ \; \mbox{.}$$ | + | <li>Vinklarna $\,-55^\circ\,$ och $\,665^\circ\,$ anger samma riktning eftersom |
| - | <li>Vinklarna $\frac{3\pi}{7}$ och $-\frac{11\pi}{7}$ anger samma riktning eftersom $$\frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7} \; \mbox{.}$$ | + | $$-55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}$$ |
| - | <li> Vinklarna $36^\circ$ och $216^\circ$ anger inte samma riktning utan motsatta riktningar eftersom $$36^\circ + 180^\circ = 216^\circ \; \mbox{.}$$ | + | |
| + | <li>Vinklarna $\,\displaystyle\frac{3\pi}{7}\,$ och $\,-\displaystyle\frac{11\pi}{7}\,$ anger samma riktning eftersom | ||
| + | $$\frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}$$ | ||
| + | |||
| + | <li> Vinklarna $\,36^\circ\,$ och $\,216^\circ\,$ anger inte samma riktning utan motsatta riktningar eftersom | ||
| + | $$36^\circ + 180^\circ = 216^\circ\,\mbox{.}$$ | ||
| </ol> | </ol> | ||
| </div> | </div> | ||
| - | ==Avståndsformlen== | + | ==Avståndsformeln== |
| - | Pythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $a$ och $b$ , och hypotenusa $c$ gäller att | + | Pythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $\,a\,$ och $\,b\,$, och hypotenusa $\,c\,$ gäller att |
| <div class="regel"> | <div class="regel"> | ||
| '''Pythagoras sats:''' | '''Pythagoras sats:''' | ||
| - | $$c^2 = a^2 + b^2 \; \mbox{.}$$ | + | $$c^2 = a^2 + b^2\,\mbox{.}$$ |
| </div> | </div> | ||
| Rad 92: | Rad 95: | ||
| Bild: figur 3.2.6 | Bild: figur 3.2.6 | ||
| - | I triangel till höger är | + | I triangeln till höger är |
| $$c^2= 3^2 + 4^2 = 9 +16 = 25$$ | $$c^2= 3^2 + 4^2 = 9 +16 = 25$$ | ||
| - | och därför är hypotenusan $c$ lika med | + | och därför är hypotenusan $\,c\,$ lika med |
| - | $$c=\sqrt{25} = 5 \; \mbox{.}$$ | + | $$c=\sqrt{25} = 5\,\mbox{.}$$ |
| </div> | </div> | ||
| Rad 103: | Rad 106: | ||
| '''Avståndsformeln:''' | '''Avståndsformeln:''' | ||
| - | Avståndet $d$ mellan två puntker med koordinater $(x, y)$ och $(a, b)$ är | + | Avståndet $\,d\,$ mellan två punkter med koordinater $\,(x, y)\,$ och $\,(a, b)\,$ är |
| - | $$d = \sqrt{(x – a)^2 + (y – b)^2} $$ | + | $$d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}$$ |
| </div> | </div> | ||
| - | Denna formel kallas för avståndsformeln. | ||
| Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna. | Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna. | ||
| Rad 112: | Rad 114: | ||
| Bild: figur 3.2.7 | Bild: figur 3.2.7 | ||
| - | Kateternas längd är lika med beloppet av skillnaden i $x$- och $y$-led mellan punkterna, d.v.s. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln. | + | Kateternas längd är lika med beloppet av skillnaden i ''x''- och ''y''-led mellan punkterna, dvs. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln. |
| <div class="exempel"> | <div class="exempel"> | ||
| Rad 118: | Rad 120: | ||
| <ol type="a"> | <ol type="a"> | ||
| - | <li>Avståndet mellan $(1,2)$ och $(3,1)$ är $$d=\sqrt{ (1-3)^2 + (2-1)^2} = \sqrt{(-2)^2 + 1^2} = \sqrt{ 4+1} = \sqrt{5} \; \mbox{.}$$ | + | <li>Avståndet mellan $\,(1,2)\,$ och $\,(3,1)\,$ är |
| - | <li>Avståndet mellan $(-1,0)$ och $(-2,-5)$ är $$d=\sqrt{ (-1-(-2))^2 + (0-(-5))^2} = \sqrt{1^2 + 5^2} = \sqrt{1+25} = \sqrt{26} \; \mbox{.}$$ | + | $$d=\sqrt{ (1-3)^2 + (2-1)^2} = \sqrt{(-2)^2 + 1^2} = \sqrt{ 4+1} = \sqrt{5}\,\mbox{.}$$ |
| + | |||
| + | <li>Avståndet mellan $\,(-1,0)\,$ och $\,(-2,-5)\,$ är | ||
| + | $$d=\sqrt{ (-1-(-2))^2 + (0-(-5))^2} = \sqrt{1^2 + 5^2} = \sqrt{1+25} = \sqrt{26}\,\mbox{.}$$ | ||
| </ol> | </ol> | ||
| Rad 127: | Rad 132: | ||
| ==Cirklar== | ==Cirklar== | ||
| - | En cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $r$ från en punkt $(a,b)$. | + | En cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $\,r\,$ från en punkt $\,(a,b)\,$. |
| Bild:figur 3.2.8 | Bild:figur 3.2.8 | ||
| - | Avståndet $r$ kallan för cirkelns radie och punkten $(a,b)$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp. | + | Avståndet $\,r\,$ kallas för cirkelns radie och punkten $\,(a,b)\,$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp. |
| - | [[Bild:3_2_10.gif]] | + | [[Bild:3_2_10.gif||center]] |
| Rad 141: | Rad 146: | ||
| En cirkelsektor är given i figuren till höger. Bild: figur 3.2.10 | En cirkelsektor är given i figuren till höger. Bild: figur 3.2.10 | ||
| <ol type="a"> | <ol type="a"> | ||
| - | <li>Bestäm cirkelbågens längd <br><br> | + | <li>Bestäm cirkelbågens längd. <br><br> |
| - | Medelpunktsvinkeln $50^\circ$ blir i radianer | + | Medelpunktsvinkeln $\,50^\circ\,$ blir i radianer |
| - | $$50^\circ= 50 \cdot 1^\circ = 50 \cdot \frac{\pi}{180} \mbox{ radianer } = \frac{5\pi}{18} \mbox{ radianer. }$$ | + | $$50^\circ= 50 \cdot 1^\circ = 50 \cdot \frac{\pi}{180}\ \mbox{ radianer } = \frac{5\pi}{18}\ \mbox{ radianer. }$$ |
| På det sätt som radianer är definerat betyder detta att cirkelbågens längd är radien multiplicerat med vinkeln mätt i radianer, | På det sätt som radianer är definerat betyder detta att cirkelbågens längd är radien multiplicerat med vinkeln mätt i radianer, | ||
| - | $$3 \cdot \frac{5\pi}{18} \mbox{ l.e. } = \frac{5\pi}{6} \mbox{ l.e. }$$ | + | $$3 \cdot \frac{5\pi}{18}\ \mbox{ l.e. } = \frac{5\pi}{6}\ \mbox{ l.e. }$$ |
| <li>Bestäm cirkelsektorns area. <br><br> | <li>Bestäm cirkelsektorns area. <br><br> | ||
| Cirkelsektorns andel av hela cirkeln är $$\frac{50^\circ}{360^\circ} = \frac{5}{36}$$ | Cirkelsektorns andel av hela cirkeln är $$\frac{50^\circ}{360^\circ} = \frac{5}{36}$$ | ||
| - | och det betyder att dess area är $\frac{5}{36}$ delar av cirkelns area som är $\pi r^2 = \pi 3^2 = 9\pi$, d.v.s. | + | och det betyder att dess area är $\,\frac{5}{36}\,$ delar av cirkelns area som är $\,\pi r^2 = \pi 3^2 = 9\pi\,$, dvs. |
| - | $$\frac{5}{36} \cdot 9\pi \mbox{ a.e. }= \frac{5\pi}{4} \mbox{ a.e. }$$ | + | $$\frac{5}{36} \cdot 9\pi\ \mbox{ a.e. }= \frac{5\pi}{4}\ \mbox{ a.e. }$$ |
| </ol> | </ol> | ||
| Rad 155: | Rad 160: | ||
| Bild:3.2.11 | Bild:3.2.11 | ||
| - | En punkt $(x,y)$ ligger på cirkeln som har medelpunkt i $(a,b)$ och radie $r$ om dess avstånd till medelpunkten är lika med $r$. Detta villkor kan formuleras med avståndsformeln som | + | En punkt $\,(x,y)\,$ ligger på cirkeln som har medelpunkt i $\,(a,b)\,$ och radie $\,r\,$ om dess avstånd till medelpunkten är lika med $\,r\,$. Detta villkor kan formuleras med avståndsformeln som |
| <div class="regel"> | <div class="regel"> | ||
| '''Cirkelns ekvation:''' | '''Cirkelns ekvation:''' | ||
| Rad 166: | Rad 171: | ||
| <ol type="a"> | <ol type="a"> | ||
| - | <li>$(x-1)^2 + (y-2)^2 = 9$ är ekvationen för en cirkel med medelpunkten i $(1,2)$ och radie $\sqrt{9} = 3$.<br><br> | + | <li>$(x-1)^2 + (y-2)^2 = 9\quad$ är ekvationen för en cirkel med medelpunkt i $\,(1,2)\,$ och radie $\,\sqrt{9} = 3\,$.<br><br> |
| - | <li>$x^2 + (y-1)^2 = 1$ kan skriva som $(x-0)^2 + (y-1)^2 = 1$ och är ekvationen för en cirkel med medelpunkten i $(0,1)$ och radie $\sqrt{1} = 1$.<br><br> | + | <li>$x^2 + (y-1)^2 = 1\quad$ kan skrivas som $\,(x-0)^2 + (y-1)^2 = 1\,$ och är ekvationen för en cirkel med medelpunkt i $\,(0,1)\,$ och radie $\,\sqrt{1} = 1\,$.<br><br> |
| - | <li>$(x+1)^2 + (y-3)^2 = 5$ kan skrivas som $(x-(-1))^2 + (y-3)^2 = 5$ och är ekvationen för en cirkel med medelpunkten i $(-1,3)$ och radie $\sqrt{5} \approx 2{,}236$. | + | <li>$(x+1)^2 + (y-3)^2 = 5\quad$ kan skrivas som $\,(x-(-1))^2 + (y-3)^2 = 5\,$ och är ekvationen för en cirkel med medelpunkt i $\,(-1,3)\,$ och radie $\,\sqrt{5} \approx 2{,}236\,$. |
| </ol> | </ol> | ||
| Rad 179: | Rad 184: | ||
| <ol type="a"> | <ol type="a"> | ||
| - | <li>Ligger punkten $(1,2)$ på cirkeln $(x-4)^2 +y^2=13$? <br><br> | + | <li>Ligger punkten $\,(1,2)\,$ på cirkeln $\,(x-4)^2 +y^2=13\,$?<br><br> |
| - | Stoppar vi in punktens koordinater $x=1$ och $y=2$ i cirkelns ekvation har vi att | + | Stoppar vi in punktens koordinater $\,x=1\,$ och $\,y=2\,$ i cirkelns ekvation har vi att |
| - | $$\mbox{VL }= (1-4)^2+2^2 =(-3)^2+2^2=9+4=13= \mbox{ HL}\; \mbox{.}$$ | + | $$\mbox{VL }= (1-4)^2+2^2 =(-3)^2+2^2=9+4=13= \mbox{ HL}\,\mbox{.}$$ |
| Eftersom punkten uppfyller cirkelns ekvation ligger punken på cirkeln. <br><br> | Eftersom punkten uppfyller cirkelns ekvation ligger punken på cirkeln. <br><br> | ||
| - | <li>Bestäm ekvationen för cirkeln som har medelpunkt i $(3,4)$ och innehåller punkten $(1,0)$.<br><br> | + | <li>Bestäm ekvationen för cirkeln som har medelpunkt i $\,(3,4)\,$ och innehåller punkten $\,(1,0)\,$.<br><br> |
| - | Eftersom punkten $(1,0)$ ska ligga på cirkeln måste cirkelns radie vara lika med avståndet från $(1,0)$ till medelpunkten $(3,4)$. Avståndsformlen ger att detta avstånd är $$c=\sqrt{(3-1)^2 + (4-0)^2 }= \sqrt{4 +16} = \sqrt{20} \; \mbox{.}$$ | + | Eftersom punkten $\,(1,0)\,$ ska ligga på cirkeln måste cirkelns radie vara lika med avståndet från $\,(1,0)\,$ till medelpunkten $\,(3,4)\,$. Avståndsformeln ger att detta avstånd är |
| + | $$c=\sqrt{(3-1)^2 + (4-0)^2 }= \sqrt{4 +16} = \sqrt{20} \, \mbox{.}$$ | ||
| Cirkelns ekvation är därför | Cirkelns ekvation är därför | ||
| $$(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}$$ | $$(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}$$ | ||
| Rad 196: | Rad 202: | ||
| '''Exempel 8''' | '''Exempel 8''' | ||
| - | Bestäm medelpunkt och radie för den cirkel vars ekvation är $x^2 + y^2 – 2x + 4y + 1 = 0$. | + | Bestäm medelpunkt och radie för den cirkel vars ekvation är $\,x^2 + y^2 – 2x + 4y + 1 = 0\,$. |
| - | Vi försöker skriva om cirkelns ekvation på formen | + | Vi ska försöka skriva om cirkelns ekvation på formen |
| $$(x – a)^2 + (y – b)^2 = r^2$$ | $$(x – a)^2 + (y – b)^2 = r^2$$ | ||
| - | för då kan vi direkt avläsa att medelpunken $(a,b)$ och radien $r$. | + | för då kan vi direkt avläsa att medelpunken är $\,(a,b)\,$ och radien är $\,r\,$. |
| - | Börja med att kvadratkomplettera termerna som innehåller $x$ i vänsterledet | + | Börja med att kvadratkomplettera termerna som innehåller $\,x\,$ i vänsterledet |
| - | $$ \underline{x^2-2x} + y^2+4y + 1 =\underline{(x-1)^2-1^2} + y^2+4y + 1$$ | + | $$ \underline{x^2-2x\vphantom{(}} + y^2+4y + 1 =\underline{(x-1)^2-1^2} + y^2+4y + 1$$ |
| (de understrukna termerna visar kvadratkompletteringen). | (de understrukna termerna visar kvadratkompletteringen). | ||
| Kvadratkomplettera sedan termerna som innehåller $y$ | Kvadratkomplettera sedan termerna som innehåller $y$ | ||
| - | $$ (x-1)^2-1^2 + \underline{y^2+4y} + 1= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1$$ | + | $$ (x-1)^2-1^2 + \underline{y^2+4y} + 1= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}$$ |
| Vänsterledet är alltså lika med | Vänsterledet är alltså lika med | ||
| $$ (x-1)^2 + (y+2)^2-4 $$ | $$ (x-1)^2 + (y+2)^2-4 $$ | ||
| - | och flyttar vi över $4$ till högerledet är cirkelns ekvation | + | och flyttar vi över 4 till högerledet är cirkelns ekvation |
| - | $$ (x-1)^2 + (y+2)^2 = 4 \; \mbox{.}$$ | + | $$ (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}$$ |
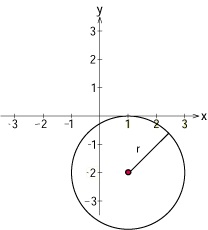
| - | Vi avläser att medelpunkten är $(1,2)$ och radien är $\sqrt{4}= 2$. | + | Vi avläser att medelpunkten är $\,(1,-2)\,$ och radien är $\,\sqrt{4}= 2\,$. |
| - | [[Bild:766790.gif]] | + | [[Bild:766790.gif||center]] |
| </div> | </div> | ||
| Rad 230: | Rad 236: | ||
| '''Tänk på att:''' | '''Tänk på att:''' | ||
| - | Lär dig att använda enhetscirkeln som ett verktyg i det trigonometriska arbetet. Avläsningar i enhetscirkeln ger dig viktiga upplysningar om diverse samband. | ||
Versionen från 8 maj 2007 kl. 12.40
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|
TeoriVinkelmåttDet finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer.
Bild: figur 3.2.1
Bild: figurer 3.2.2 och figurer 3.2.3
Exempel 1
I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än 360°. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv. Bild: Figur 3.2.4 Exempel 2
AvståndsformelnPythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $\,a\,$ och $\,b\,$, och hypotenusa $\,c\,$ gäller att Pythagoras sats: $$c^2 = a^2 + b^2\,\mbox{.}$$ Bild: figur 3.2.5 Exempel 3 Bild: figur 3.2.6 I triangeln till höger är $$c^2= 3^2 + 4^2 = 9 +16 = 25$$ och därför är hypotenusan $\,c\,$ lika med $$c=\sqrt{25} = 5\,\mbox{.}$$ Pythagoras sats kan användas för att beräkna avståndet mellan två punkter i ett koordinatsystem. Avståndsformeln: Avståndet $\,d\,$ mellan två punkter med koordinater $\,(x, y)\,$ och $\,(a, b)\,$ är $$d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}$$ Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna. Bild: figur 3.2.7 Kateternas längd är lika med beloppet av skillnaden i x- och y-led mellan punkterna, dvs. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln. Exempel 4
Interaktivt experiment: Här kan du experimentera med avståndsformeln och Pythagoras sats CirklarEn cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $\,r\,$ från en punkt $\,(a,b)\,$. Bild:figur 3.2.8 Avståndet $\,r\,$ kallas för cirkelns radie och punkten $\,(a,b)\,$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp.
Exempel 5 En cirkelsektor är given i figuren till höger. Bild: figur 3.2.10
Bild:3.2.11 En punkt $\,(x,y)\,$ ligger på cirkeln som har medelpunkt i $\,(a,b)\,$ och radie $\,r\,$ om dess avstånd till medelpunkten är lika med $\,r\,$. Detta villkor kan formuleras med avståndsformeln som Cirkelns ekvation: $$(x – a)^2 + (y – b)^2 = r^2$$ och kallas för cirkelns ekvation. Exempel 6
Bild: figur 3.2-12-14 Exempel 7
Bild: 3.2.15 och 3.2.16 Exempel 8 Bestäm medelpunkt och radie för den cirkel vars ekvation är $\,x^2 + y^2 – 2x + 4y + 1 = 0\,$.
Börja med att kvadratkomplettera termerna som innehåller $\,x\,$ i vänsterledet $$ \underline{x^2-2x\vphantom{(}} + y^2+4y + 1 =\underline{(x-1)^2-1^2} + y^2+4y + 1$$ (de understrukna termerna visar kvadratkompletteringen). Kvadratkomplettera sedan termerna som innehåller $y$ $$ (x-1)^2-1^2 + \underline{y^2+4y} + 1= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}$$ Vänsterledet är alltså lika med $$ (x-1)^2 + (y+2)^2-4 $$ och flyttar vi över 4 till högerledet är cirkelns ekvation $$ (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}$$ Vi avläser att medelpunkten är $\,(1,-2)\,$ och radien är $\,\sqrt{4}= 2\,$.
Råd för inläsning Tänk på att:
Lästips för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om: Sammanfattning av Geometri B ur Theducations gymnasielexikon Läs mer om Pythagoras sats på svenska Wikipedia Läs mer i Mathworld om cirkeln
Interaktivt experiment: sinus och cosinus i enehtscirkeln (Flash) Experimentera med Randvinkelsatsen
|
|