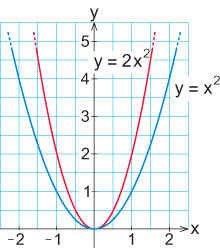
2.3 Andragradsuttryck
Sommarmatte 1
| Versionen från 23 april 2007 kl. 16.26 (redigera) Lina (Diskussion | bidrag) (→Parabler) ← Gå till föregående ändring |
Versionen från 23 april 2007 kl. 16.37 (redigera) (ogör) Lina (Diskussion | bidrag) (→Parabler) Gå till nästa ändring → |
||
| Rad 162: | Rad 162: | ||
| $$y=x^2-2x+5$$ | $$y=x^2-2x+5$$ | ||
| $$y=4-3x^2$$ | $$y=4-3x^2$$ | ||
| - | $$y=\frac1}{5}x^2 +3x$$ | + | $$y=\frac{1}{5}x^2 +3x$$ |
| är exempel på andragradsfunktioner. Allmänt kan en andragradsfunktion skrivas som | är exempel på andragradsfunktioner. Allmänt kan en andragradsfunktion skrivas som | ||
| Rad 194: | Rad 194: | ||
| </div> | </div> | ||
| + | Med kvaratkomplettering kan vi behandla alla typer av parabler. | ||
| + | <div class="exempel"> | ||
| + | '''Exempel 6''' | ||
| + | Skissera parabeln $y=x^2+2x+2$. | ||
| - | Hur gör man för att enklast kunna beskriva utseendet för en sådan andragradskurva? | ||
| - | Rent generellt så har en andragradskurva enbart ett lokalt minimum eller maximum. | ||
| - | Samtidigt kan den maximalt skära ''x''-axeln på två ställen och ''y''-axeln på | ||
| - | ett ställe. | ||
| + | Om högerledet kvadratkompletteras | ||
| + | $$x^2 +2x+2 = (x+1)^2 -1^2 +2 = (x+1)^2+1$$ | ||
| + | så ser vi från det resulterande uttrycket $y= (x+1)^2+1$ att parabeln är förskjuten en enhet åt vänster i $x$-led jämfört med $y=x^2$ (eftersom det står $(x+1)^2$ istället för $x^2$) och en enhet uppåt i $y$-led. | ||
| + | Bild: figur 3.1.5b<br><br> | ||
| - | '''Hur skall man kunna hitta dessa punkter?''' | + | </div> |
| + | <div class="exempel"> | ||
| + | '''Exempel 7''' | ||
| - | För enkelhetsskull så antar vi ovan att $a=1$, d.v.s. | ||
| - | $y=x^2+bx+c$ Vi vill kunna skriva formen för | ||
| - | en andragradskruva som en jämn kvadrat plus en konstant. Efter kvadratkomplettering ser att vi kan skriva | ||
| - | uttrycket som | ||
| - | |||
| - | |||
| - | |||
| - | $ | ||
| - | y=\left(x+\displaystyle \frac{b}{2}\right)^2 +c-\displaystyle \frac{b^2}{4}. | ||
| - | $ | ||
| - | |||
| - | |||
| - | Detta uttyck kan minimalt bli $ c- \displaystyle \frac{b^2}{4} $ eftersom kvadraten inte kan bli mindre än 0. | ||
| - | Vi ser alltså att minpunkten blir | ||
| - | |||
| - | |||
| - | |||
| - | $ | ||
| - | (x,y)=\left(-\displaystyle \frac{b}{2},c-\displaystyle \frac{b^2}{4}\right) | ||
| - | $ | ||
| - | |||
| - | |||
| - | I motsvarande fall om $a=-1$ så får vi att $\;y=-x^2+bx+c \;$ har maxpunkt i $(b/2,c+b^2/4)$. | ||
| - | Skärning med ''x''-axeln fås då ''y''=0 och det är inte säkert att det är | ||
| - | uppfyllt dvs sambandet har ett minimivärde som är större än 0. | ||
| - | Vi har nu en kurva med ekvation | ||
| - | |||
| - | |||
| - | |||
| - | $ | ||
| - | y=ax^2+bx+c. | ||
| - | $ | ||
| - | |||
| - | |||
| - | Efter kvadratkomplettering så inser vi att konstanten $a$ bestämmer formen på kurvan medan | ||
| - | $a,b \mbox{ och } c$ alla är med och bestämmer positionen av minimi-/maximivärdet hos kurvan. | ||
| - | Eftersom en andragradskurva enbart har en maximi eller minimi-punkt så är det ganska enkelt att bestämma formen | ||
| - | hos kurvan. För enkelhetsskull antar vi nu att $b \mbox{ och } c = 0.$ Vi har alltså ett samband | ||
| - | |||
| - | |||
| - | |||
| - | $ | ||
| - | y=ax^2 | ||
| - | $ | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | Polariteten hos $a$ bestämmer om kurvan har ett maxvärde eller minvärde dvs om den pekar | ||
| - | uppåt eller nedåt. Vi ser att koefficienten $ a $ trycker ihop/drar ut kurvan $ y=x^2,$ | ||
| - | beroende på om $a<1$ eller om $ a>1$. | ||
| - | <p align="center"><img src="ppStdFiles2261/766663.gif" hspace='0' vspace='0' /><br clear='all' /> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | Position i vertikalled (dvs i y-led) styrs av konstanten $c$. Vi låter nu $a=1$ | ||
| - | och $b=0$ ovan. Vi ser att | ||
| - | $ y=x^2+2 $ har minsta värde 2 medan $ y=x^2 $ har minsta värde 0. | ||
| - | $ y=x^2$ kan alltså enkelt ritas i ett koordinatsystem genom att föorflytta | ||
| - | $ y=x^2$ två längdenheter i positiv ''y''-riktning. | ||
| - | <p align="center"><img src="ppStdFiles2261/766664.gif" hspace='0' vspace='0' /><br clear='all' /> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | Position i horisontalled styrs av konstanten ''b''. Låt nu ''a''=1 och ''c''=0 ovan. Vi har då kurvan | ||
| - | $ y=x^2+bx$. | ||
| - | |||
| - | |||
| - | |||
| - | Om vi kvadratkompletterar så får vi att $ y=\left(x+\displaystyle \frac{b}{2}\right)^2-\displaystyle \frac{b^2}{4} $ | ||
| - | Vi ser alltså att $ y $ kan vara minimalt $ -\,\displaystyle \frac{b^2}{4} $ då | ||
| - | $ x=-\,\displaystyle \frac{b}{2}$. Vi kan alltså sammanfatta att koefficienten $b$ | ||
| - | gjorde att minpunkten flyttades från origo till punkten $ \left(-\,\displaystyle \frac{b}{2},-\,\displaystyle \frac{b^2}{4}\right) $ | ||
| - | <p align="center"><img src="ppStdFiles2261/766668.gif" hspace='0' vspace='0' /><br clear='all' /> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | Vad som också kan vara av intresse är skärningspunkter mellan en andragradskurva och ''x''-axeln. | ||
| - | |||
| - | |||
| - | Vi har ovan noterat att det inte behöver vara så att en andragradskurva skär ''x''-axeln. | ||
| - | Det kan också vara att den tangerar ''x''-axeln eller att den skär ''x''-axeln i två punkter. | ||
| - | |||
| - | |||
| - | Antag att vi har en andragradskurva $y=ax^2+bx+c$. Skärningspunkter med ''x''-axeln | ||
| - | fås genom att lösa ekvationen $ y=0 $ dvs $ ax^2+bx+c = 0$. | ||
| - | Observera att $y=0$ för alla punkter på ''x''-axeln. | ||
| + | Bild: figur 3.1.6b<br><br> | ||
| + | </div> | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 5''' | + | '''Exempel 8''' |
| - | <ol type="a"> | + | |
| - | <li>$matte$ <br><br> | + | |
| - | <li>text | + | |
| - | </ol> | + | |
| - | </div | ||
| - | |||
| - | Bestäm skärningspunkter med ''x''-axeln och $ | ||
| - | y=x^2-4x-5. | ||
| - | $ | ||
| - | '''Lösning:''' | ||
| - | + | Bild: figur 3.1.7b<br><br> | |
| - | $ | + | |
| - | y=0 $ på x-axeln. Vi har alltså att lösa ekvationen $ x^2-4x-5=0. | + | |
| - | $ | + | |
| - | + | </div> | |
| - | Kvadratkomplettering ger att: | + | |
| - | + | ||
| - | + | ||
| - | $ | + | |
| - | x^2-4x-5 = (x-2)^2-4-5=(x-2)^2-3^2 | + | |
| - | $={konjugatregeln}= | + | |
| - | + | ||
| - | + | ||
| - | $ | + | |
| - | (x-2-3)(x-2+3)=(x-5)(x+1) $ vilket är 0 då $ x=5 $ eller $ x=-1. | + | |
| - | $ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | '''Svar: ''' | + | |
| - | $\left\{ \matrix {x_1=5 \cr x_2=-1 } \right.$ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | |} | + | |
Versionen från 23 april 2007 kl. 16.37
2.3 AndragradsuttryckInnehåll:
Läromål: Efter detta avsnitt ska du ha lärt dig att:
|
||
TeoriAndragradsekvationerEn andragradsekvation är en ekvation som kan skrivas som $$x^2+px+q=0$$ där $x$ är den obekanta och $p$ och $q$ är konstanter.
Ekvationen $x^2=a$ där $a$ är ett postivt tal har två lösningar (rötter) $x=\sqrt{a}$ och $x=-\sqrt{a}$. Exempel 1
Exempel 2
För att lösa allmänna andragradsekvationer använder vi en teknik som kallas kvadratkomplettering Om vi betraktar kvaderingsregeln $$x^2 + 2ax + a^2 = (a+x)^2$$ och subtraherar $a^2$ från båda led så får vi Kvadratkomplettering: $$x^2 +2ax = (x+a)^2 -a^2$$ Detta är formeln för kvadratkomplettering. Exempel 3
Tips: Tänk på att man alltid kan pröva lösningar till en ekvation genom att sätta in värdet och se om likheten blir uppfylld. Man gör detta för att upptäcka eventuella slarvfel. För exemplet ovan har vi två fall att pröva. Vi kallar vänster- och högerleden för VL respektive HL: x = 0 medför $ \mbox{VL} = 0^2 - 4\cdot0 = 0 = \mbox{HL} $ x = 4 medför $ \mbox{VL} = 4^2 - 4\cdot4 = 0 = \mbox{HL} $ I båda fallen kommer vi fram till VL = HL. Ekvationen är alltså uppfylld i båda fallen. x = 0 och x = 4 är lösningar till ekvationen. Med kvadratkomplettering går det att visa att den allmänna andragradsekvationen $$x^2+px+q=0$$ har lösningarna $$x = - \displaystyle\frac{p}{2} \pm \sqrt{\left(\displaystyle\frac{p}{2}\right)^2-q}$$ förutsatt att uttrycket under rottecknet inte är negativt. Ibland kan man faktorisera ekvationer och direkt se vilka lösningarna är. Exempel 4 Exempeltext, använd nedanstående numrering
ParablerFunktionerna $$y=x^2-2x+5$$ $$y=4-3x^2$$ $$y=\frac{1}{5}x^2 +3x$$ är exempel på andragradsfunktioner. Allmänt kan en andragradsfunktion skrivas som $$y=ax^2+bx+c$$ där $a$, $b$ och $c$ är konstanter och där $a\ne0$. Grafen till en andragradsfunktion kallas för en parabel och figurerna visar utseendet för två typexempel $y=x^2$ och $y=-x^2$. Bild: figur 3.1.1b och 3.1.2b Eftersom uttrycket $x^2$ är som minst när $x=0$ har parabeln $y=x^2$ ett maximum för $x=0$. Notera också att parablerna ovan är symmetriska kring $y$-axeln eftersom värdet på $x^2$ inte beror på vilket tecken $x$ har. Exempel 5
Med kvaratkomplettering kan vi behandla alla typer av parabler. Exempel 6 Skissera parabeln $y=x^2+2x+2$.
Bild: figur 3.1.5b Exempel 7
Bild: figur 3.1.6b Exempel 8
Bild: figur 3.1.7b
Råd för inläsning Tänk på att: Att ställa upp ekvationer är som att översätta från ett språk till ett annat. Denna jämförelse användes av Newton i hans Arithmetica Universalis. Kanske kan den bidra till att öka förståelsen för de svårigheter som både studenter och lärare ställs inför, ibland. Lägg ner mycket tid på algebra! Algebra är matematikens alfabet. När du väl har förstått algebra, kommer din förståelse av statistik, yta, volym och geometri vara mycket större.
för dig som vill fördjupa dig ytterligare eller skulle vilja ha en längre förklaring Läs mer om andragradsekvationer på engelska Wikipedia Läs mer om andragradsekvationer i MathWorld 101 uses of a quadratic equation - by Chris Budd and Chris Sangwin
Experimentera - När väger ekvationens led lika? Träna på andragradsekvationer och slå ditt personliga rekord.
|
|