4.1 Vinklar och cirklar
Sommarmatte 1
4.1 Vinklar och cirklarInnehåll:
Läromål: Efter detta avsnitt ska du ha lärt dig att:
|
||
TeoriVinkelmåttDet finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer.
Bild: figur 3.2.1
Bild: figurer 3.2.2 och figurer 3.2.3
Exempel 1
I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än $360^\circ$. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv. Bild: Figur 3.2.4 Exempel 2
AvståndsformlenPythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $a$ och $b$ , och hypotenusa $c$ gäller att $$c^2 = a^2 + b^2 \; \mbox{.}$$ Bild: figur 3.2.5 Exempel 3 Bild: figur 3.2.6 I triangel till höger är $$c^2= 3^2 + 4^2 = 9 +16 = 25$$ och därför är hypotenusan $c$ lika med $$c=\sqrt{25} = 5 \; \mbox{.}$$ Pythagoras sats kan användas för att beräkna avståndet mellan två punkter i ett koordinatsystem. Avståndsformeln: Avståndet $d$ mellan två puntker med koordinater $(x, y)$ och $(a, b)$ är $$d = \sqrt{(x – a)^2 + (y – b)^2} $$ Denna formel kallas för avståndsformeln. Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna. Bild: figur 3.2.7 Kateternas längd är lika med beloppet av skillnaden i $x$- och $y$-led mellan punkterna, d.v.s. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln. Exempel 4
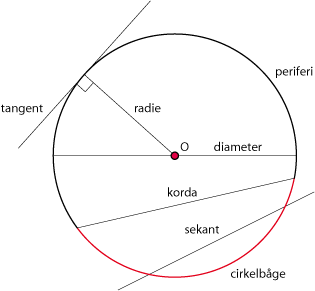
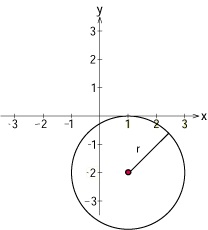
Interaktivt experiment: Här kan du experimentera med avståndsformeln och Pythagoras sats CirklarEn cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $r$ från en punkt $(a,b)$. Bild:figur 3.2.8 Avståndet $r$ kallan för cirkelns radie och punkten $(a,b)$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp.
Exempel 5 En cirkelsektor är given i figuren till höger. Bild: figur 3.2.10
Bild:3.2.11 En punkt $(x,y)$ ligger på cirkeln som har medelpunkt i $(a,b)$ och radie $r$ om dess avstånd till medelpunkten är lika med $r$. Detta villkor kan formuleras med avståndsformeln som Cirkelns ekvation: $$(x – a)^2 + (y – b)^2 = r^2$$ och kallas för cirkelns ekvation. Exempel 6
Bild: figur 3.2-12-14 Exempel 7
Bild: 3.2.15 och 3.2.16 Exempel 8 Bestäm medelpunkt och radie för den cirkel vars ekvation är $x^2 + y^2 – 2x + 4y + 1 = 0$.
Börja med att kvadratkomplettera termerna som innehåller $x$ i vänsterledet $$ \underline{x^2-2x} + y^2+4y + 1 =\underline{(x-1)^2-1^2} + y^2+4y + 1$$ (de understrukna termerna visar kvadratkompletteringen). Kvadratkomplettera sedan termerna som innehåller $y$ $$ (x-1)^2-1^2 + \underline{y^2+4y} + 1= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1$$ Vänsterledet är alltså lika med $$ (x-1)^2 + (y+2)^2-4 $$ och flyttar vi över $4$ till högerledet är cirkelns ekvation $$ (x-1)^2 + (y+2)^2 = 4 \; \mbox{.}$$ Vi avläser att medelpunkten är $(1,2)$ och radien är $\sqrt{4}= 2$.
Råd för inläsning Tänk på att: Lär dig att använda enhetscirkeln som ett verktyg i det trigonometriska arbetet. Avläsningar i enhetscirkeln ger dig viktiga upplysningar om diverse samband.
för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om: Sammanfattning av Geometri B ur Theducations gymnasielexikon Läs mer om Pythagoras sats på svenska Wikipedia Läs mer i Mathworld om cirkeln
Interaktivt experiment: sinus och cosinus i enehtscirkeln (Flash) Experimentera med Randvinkelsatsen
|
|