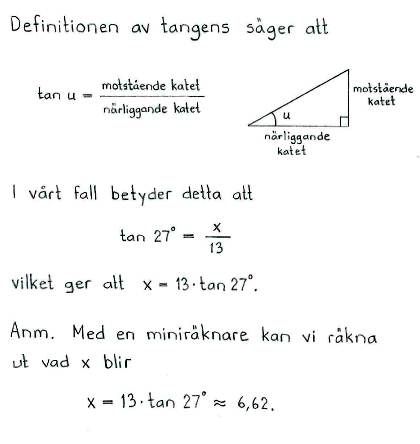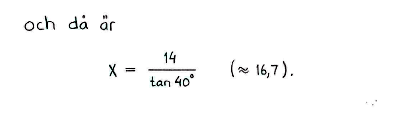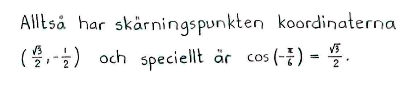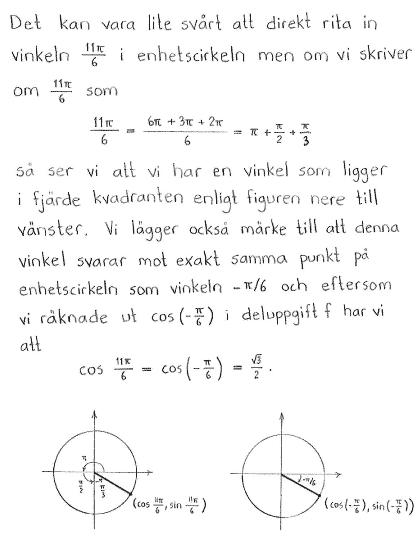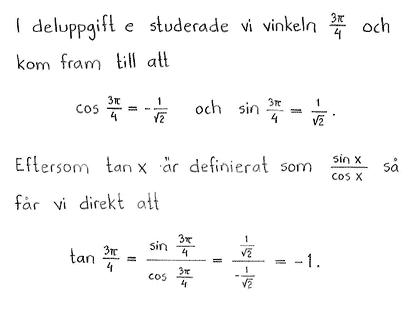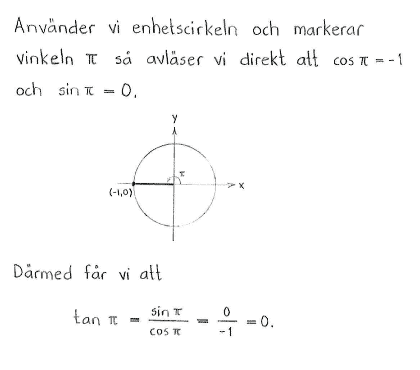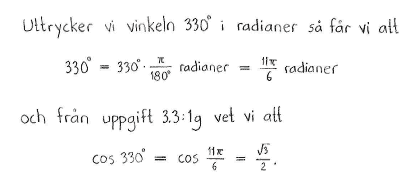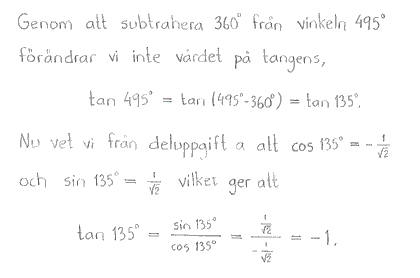Sommarmatte 1
Övning 4.2:1
Bestäm längden av sidan som är markerad med $x$ uttryckt med hjälp av de trigonometriska funktionerna.
| a) |
BILD |
b) |
BILD |
c) |
BILD |
d) |
BILD |
e) |
BILD |
f) |
BILD |
|
Facit
Facit till alla delfrågorna
| a) |
$x=13\cdot\tan {27 ^\circ} \approx 6,62$ |
b) |
$x=25\cdot\cos {32 ^\circ} \approx 21,2$ |
c) |
$x=\displaystyle\frac{14}{\tan {40 ^\circ}} \approx 16,7$ |
|
| d) |
$x=\displaystyle\frac{16}{\cos {20 ^\circ}} \approx 17,0$ |
e) |
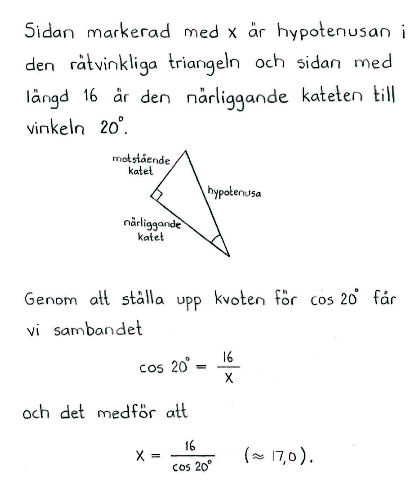
$x=\displaystyle\frac{11}{\sin {35 ^\circ}} \approx 19,2$ |
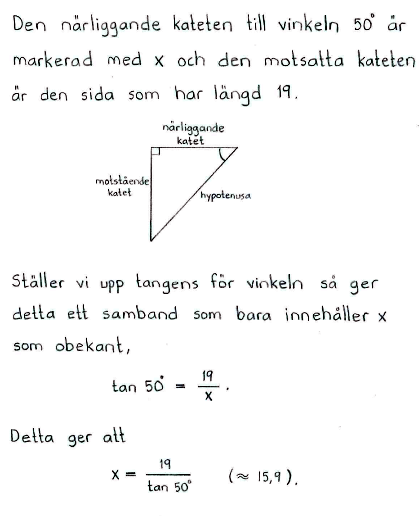
f) |
$x=\displaystyle\frac{19}{\tan {50 ^\circ}} \approx 15,9$ |
|
Lösning a
Lösning till delfråga a
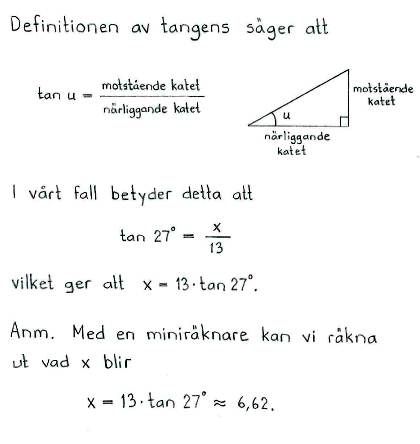
Lösning b
Lösning till delfråga b

Lösning c
Lösning till delfråga c

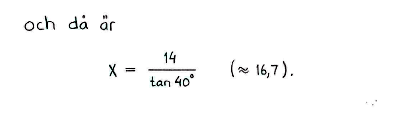
Lösning d
Lösning till delfråga d
Lösning e
Lösning till delfråga e
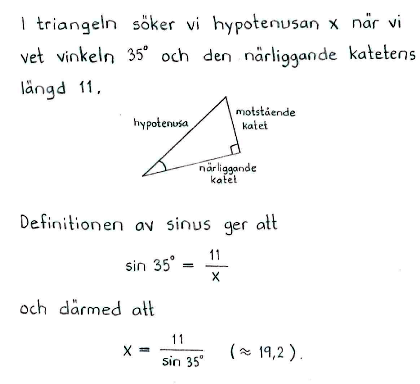
Lösning f
Lösning till delfråga f
Övning 4.2:2
Bestäm en trigonometrisk ekvation dom vinkeln $v$ uppfyller.
| a) |
BILD |
b) |
BILD |
c) |
BILD |
d) |
BILD |
e) |
BILD |
f) |
BILD |
|
Facit
Facit till alla delfrågorna
| a) |
$\tan v=\displaystyle\frac{2}{5}$ |
b) |
$\sin v=\displaystyle\frac{7}{11}$ |
|
| c) |
$\cos v=\displaystyle\frac{5}{7}$ |
d) |
$\sin v=\displaystyle\frac{3}{5}$ |
|
| e) |
$v=30 ^\circ$ |
f) |
$\sin \displaystyle\frac{v}{2}=\displaystyle\frac{1}{3}$ |
|
Lösning a
Lösning till delfråga a

Lösning b
Lösning till delfråga b
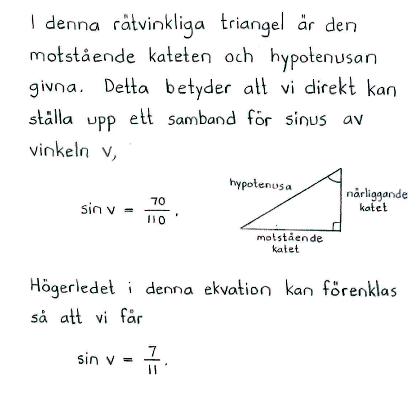
Lösning c
Lösning till delfråga c

Lösning d
Lösning till delfråga d

Lösning e
Lösning till delfråga e

Lösning f
Lösning till delfråga f
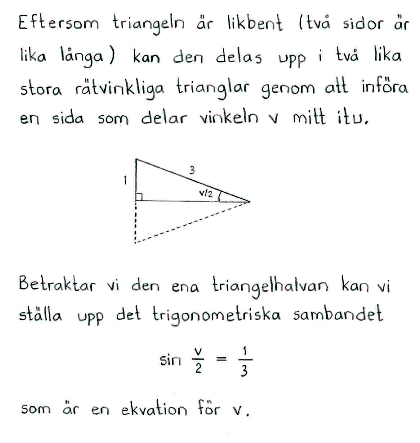
Övning 4.2:3
Bestäm
| $\textrm{a) }$ |
$\sin{\left(-\displaystyle \frac{\pi}{2}\right)}$ |
$\textrm{b) }$ |
$\cos{2\pi}$ |
$\textrm{c) }$ |
$\sin{9\pi}$ |
|
| $\textrm{d) }$ |
$\cos{\displaystyle \frac{7\pi}{2}}$ |
$\textrm{e) }$ |
$\sin{\displaystyle \frac{3\pi}{4}}$ |
$\textrm{f) }$ |
$\cos{\left(-\displaystyle \frac{\pi}{6}\right)}$ |
|
Facit
Facit till alla delfrågorna
| $\textrm{a) }$ |
$-1$ |
$\textrm{b) }$ |
$1$ |
$\textrm{c) }$ |
$0$ |
|
| $\textrm{d) }$ |
$0$ |
$\textrm{e) }$ |
$\displaystyle \frac{1}{\sqrt{2}}$ |
$\textrm{f) }$ |
$\displaystyle \frac{\sqrt{3}}{2}$ |
|
Lösning a
Lösning till delfråga a

Lösning b
Lösning till delfråga b
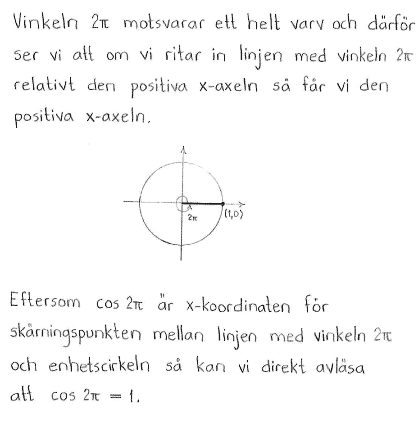
Lösning c
Lösning till delfråga c

Lösning d
Lösning till delfråga d

Lösning e
Lösning till delfråga e


Lösning f
Lösning till delfråga f

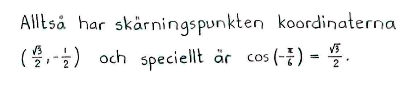
Övning 4.2:4
Bestäm
| a) |
$\cos{\displaystyle \frac{11\pi}{6}}$ |
b) |
$\cos{\displaystyle \frac{11\pi}{3}}$ |
c) |
$\tan{\displaystyle \frac{3\pi}{4}}$ |
|
| d) |
$\tan{\pi}$ |
e) |
$\tan{\displaystyle \frac{7\pi}{6}}$ |
f) |
$\tan{\left(-\displaystyle \frac{5\pi}{3}\right)}$ |
|
Facit
Facit till alla delfrågorna
| a) |
$\displaystyle \frac{\sqrt{3}}{2}$ |
b) |
$\displaystyle \frac{1}{2}$ |
c) |
$-1$ |
|
| d) |
$0$ |
e) |
$\displaystyle \frac{1}{\sqrt{3}}$ |
f) |
$\sqrt{3}$ |
|
Lösning a
Lösning till delfråga a
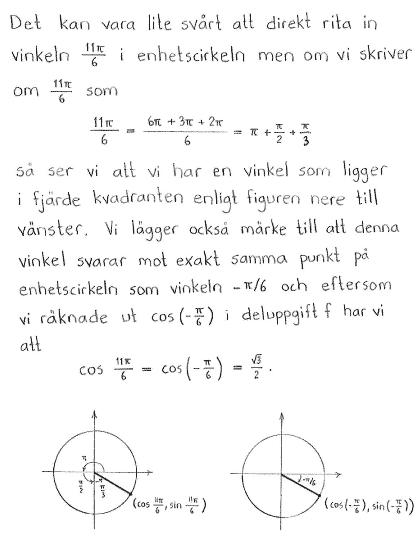
Lösning b
Lösning till delfråga b


Lösning c
Lösning till delfråga c
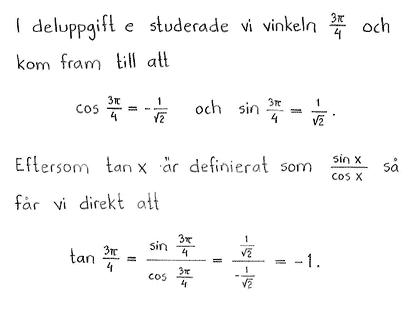
Lösning d
Lösning till delfråga d
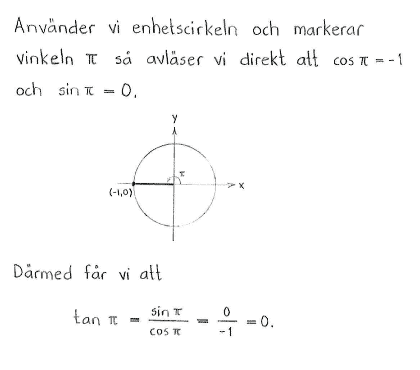
Lösning e
Lösning till delfråga e

Lösning f
Lösning till delfråga f

Övning 4.2:5
Bestäm
| $\textrm{a) }$ |
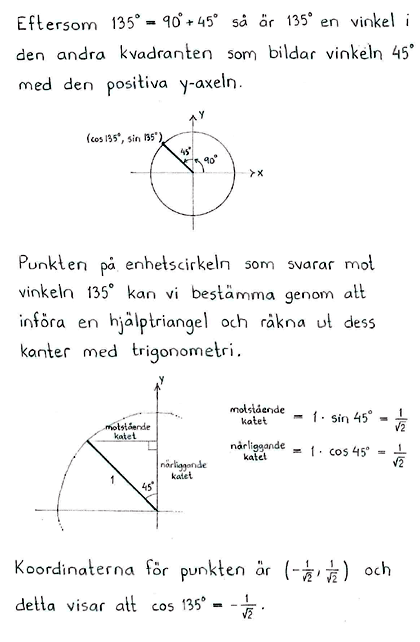
$\cos{135^\circ}$ |
$\textrm{b) }$ |
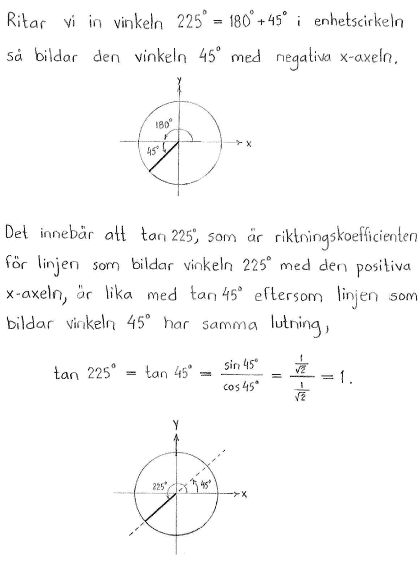
$\tan{225^\circ}$ |
$\textrm{c) }$ |
$\cos{330^\circ}$ |
$\textrm{d) }$ |
$\tan{495^\circ}$ |
|
Facit
Facit till alla delfrågorna
| $\textrm{a) }$ |
$-\displaystyle \frac{1}{\sqrt{2}}$ |
$\textrm{b) }$ |
$1$ |
$\textrm{c) }$ |
$\displaystyle \frac{\sqrt{3}}{2}$ |
$\textrm{d) }$ |
$-1$ |
|
Lösning a
Lösning till delfråga a
Lösning b
Lösning till delfråga b
Lösning c
Lösning till delfråga c
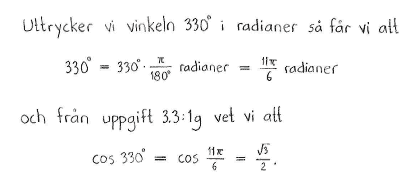
Lösning d
Lösning till delfråga d
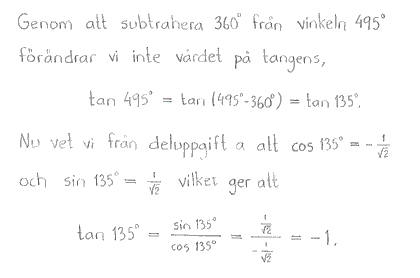
Övning 4.2:6
Bestäm längden av sidan som är markerad med $x$.
Övning 4.2:7
För att mäta upp bredden av en älv mäter vi från två punkter A och B längs den ena raka stranden vinkeln till ett träd C på motsatt sida älven. Hur bred är älven om måtten i figuren gäller?
Facit
| $\displaystyle\frac{100}{\sqrt{3}-1}$ m $\approx 136,6$ m |
|
Övning 4.2:8
En stång med längd $l$ är upphängd i två linor med längd $a$ resp. $b$ enligt figuren. Linorna bildar vinklar $\alfa$ resp. $\beta$ med vertikalen. Bestäm en trignometrisk ekvation för vinkeln $\gamma$ som stången bildar med vertikalen.
Facit
| $l\cos \gamma=a \cos \alfa - b\cos \beta $ |
|
Övning 4.2:9
Bestäm längden av sidan som är markerad med $x$.