Teori
Vinkelmått
Det finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer.
- Grader. Om ett helt varv delas in i 360 delar, så kallas varje del 1 grad. Beteckningen för grader är $ ^\circ$.
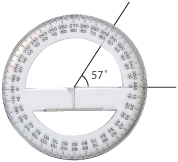
- Radianer. Ett annat sätt att mäta vinklar är att använda längden av vinkelns cirkelbåge i förhållande till radien som mått på vinkeln. Detta vinkelmått kallas för radian. Ett varv är alltså $\,2\pi\,$ radianer eftersom cirkelns omkrets är $\,2\pi r\,$, där $\,r\,$ är cirkelns radie.
Bild: figurer 3.2.2 och figurer 3.2.3
Ett helt varv är $\,360^\circ\,$ eller $\,2\pi\,$ radianer och det gör att
$$\eqalign{&1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radianer } = \frac{\pi}{180}\ \mbox{ radianer,}\cr &1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ = \frac{180^\circ}{\pi}\,\mbox{.}}$$
Dessa omvandlingsfaktorer kan användas för att konvertera mellan grader och radianer.
Exempel 1
- $30^\circ = 30 \cdot 1^\circ = 30 \cdot \displaystyle \frac{\pi}{180}\ \mbox{ radianer } = \displaystyle \frac{\pi}{6}\ \mbox{ radianer }$
- $ \displaystyle \frac{\pi}{8}\ \mbox { radianer } = \displaystyle \frac{\pi}{8} \cdot (1 \; \mbox{radian}\,) = \displaystyle \frac{\pi}{8} \cdot \displaystyle \frac{180^\circ}{\pi} = 22{,}5^\circ$
I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än 360°. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv.
Bild: Figur 3.2.4
Exempel 2
- Vinklarna $\,-55^\circ\,$ och $\,665^\circ\,$ anger samma riktning eftersom
$$-55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}$$
- Vinklarna $\,\displaystyle\frac{3\pi}{7}\,$ och $\,-\displaystyle\frac{11\pi}{7}\,$ anger samma riktning eftersom
$$\frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}$$
- Vinklarna $\,36^\circ\,$ och $\,216^\circ\,$ anger inte samma riktning utan motsatta riktningar eftersom
$$36^\circ + 180^\circ = 216^\circ\,\mbox{.}$$
Avståndsformeln
Pythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter $\,a\,$ och $\,b\,$, och hypotenusa $\,c\,$ gäller att
Pythagoras sats:
$$c^2 = a^2 + b^2\,\mbox{.}$$
Bild: figur 3.2.5
Exempel 3
Bild: figur 3.2.6
I triangeln till höger är
$$c^2= 3^2 + 4^2 = 9 +16 = 25$$
och därför är hypotenusan $\,c\,$ lika med
$$c=\sqrt{25} = 5\,\mbox{.}$$
Pythagoras sats kan användas för att beräkna avståndet mellan två punkter i ett koordinatsystem.
Avståndsformeln:
Avståndet $\,d\,$ mellan två punkter med koordinater $\,(x, y)\,$ och $\,(a, b)\,$ är
$$d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}$$
Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna.
Bild: figur 3.2.7
Kateternas längd är lika med beloppet av skillnaden i x- och y-led mellan punkterna, dvs. $|x-a|$ respektive $|y-b|$. Pythagoras sats ger sedan avståndsformeln.
Exempel 4
- Avståndet mellan $\,(1,2)\,$ och $\,(3,1)\,$ är
$$d=\sqrt{ (1-3)^2 + (2-1)^2} = \sqrt{(-2)^2 + 1^2} = \sqrt{ 4+1} = \sqrt{5}\,\mbox{.}$$
- Avståndet mellan $\,(-1,0)\,$ och $\,(-2,-5)\,$ är
$$d=\sqrt{ (-1-(-2))^2 + (0-(-5))^2} = \sqrt{1^2 + 5^2} = \sqrt{1+25} = \sqrt{26}\,\mbox{.}$$
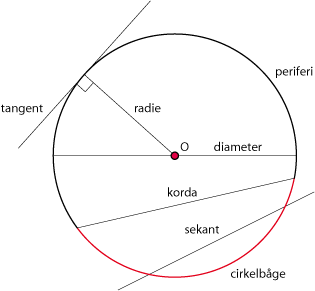
Cirklar
En cirkel består av alla punkter som befinner sig på ett visst fixt avstånd $\,r\,$ från en punkt $\,(a,b)\,$.
Bild:figur 3.2.8
Avståndet $\,r\,$ kallas för cirkelns radie och punkten $\,(a,b)\,$ för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp.
Exempel 5
En cirkelsektor är given i figuren till höger. Bild: figur 3.2.10
- Bestäm cirkelbågens längd.
Medelpunktsvinkeln $\,50^\circ\,$ blir i radianer
$$50^\circ= 50 \cdot 1^\circ = 50 \cdot \frac{\pi}{180}\ \mbox{ radianer } = \frac{5\pi}{18}\ \mbox{ radianer. }$$
På det sätt som radianer är definierat betyder detta att cirkelbågens längd är radien multiplicerat med vinkeln mätt i radianer,
$$3 \cdot \frac{5\pi}{18}\ \mbox{ l.e. } = \frac{5\pi}{6}\ \mbox{ l.e. }$$
- Bestäm cirkelsektorns area.
Cirkelsektorns andel av hela cirkeln är $$\frac{50^\circ}{360^\circ} = \frac{5}{36}$$
och det betyder att dess area är $\,\frac{5}{36}\,$ delar av cirkelns area som är $\,\pi r^2 = \pi 3^2 = 9\pi\,$, dvs.
$$\frac{5}{36} \cdot 9\pi\ \mbox{ a.e. }= \frac{5\pi}{4}\ \mbox{ a.e. }$$
Bild:3.2.11
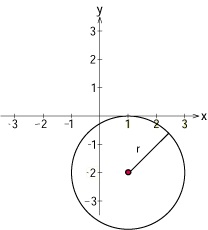
En punkt $\,(x,y)\,$ ligger på cirkeln som har medelpunkt i $\,(a,b)\,$ och radie $\,r\,$ om dess avstånd till medelpunkten är lika med $\,r\,$. Detta villkor kan formuleras med avståndsformeln som
Cirkelns ekvation:
$$(x – a)^2 + (y – b)^2 = r^2\,\mbox{.}$$
Exempel 6
- $(x-1)^2 + (y-2)^2 = 9\quad$ är ekvationen för en cirkel med medelpunkt i $\,(1,2)\,$ och radie $\,\sqrt{9} = 3\,$.
- $x^2 + (y-1)^2 = 1\quad$ kan skrivas som $\,(x-0)^2 + (y-1)^2 = 1\,$ och är ekvationen för en cirkel med medelpunkt i $\,(0,1)\,$ och radie $\,\sqrt{1} = 1\,$.
- $(x+1)^2 + (y-3)^2 = 5\quad$ kan skrivas som $\,(x-(-1))^2 + (y-3)^2 = 5\,$ och är ekvationen för en cirkel med medelpunkt i $\,(-1,3)\,$ och radie $\,\sqrt{5} \approx 2{,}236\,$.
Bild: figur 3.2-12-14
Exempel 7
- Ligger punkten $\,(1,2)\,$ på cirkeln $\,(x-4)^2 +y^2=13\,$?
Stoppar vi in punktens koordinater $\,x=1\,$ och $\,y=2\,$ i cirkelns ekvation har vi att
$$\mbox{VL }= (1-4)^2+2^2 =(-3)^2+2^2=9+4=13= \mbox{ HL}\,\mbox{.}$$
Eftersom punkten uppfyller cirkelns ekvation ligger punken på cirkeln.
- Bestäm ekvationen för cirkeln som har medelpunkt i $\,(3,4)\,$ och innehåller punkten $\,(1,0)\,$.
Eftersom punkten $\,(1,0)\,$ ska ligga på cirkeln måste cirkelns radie vara lika med avståndet från $\,(1,0)\,$ till medelpunkten $\,(3,4)\,$. Avståndsformeln ger att detta avstånd är
$$c=\sqrt{(3-1)^2 + (4-0)^2 }= \sqrt{4 +16} = \sqrt{20} \, \mbox{.}$$
Cirkelns ekvation är därför
$$(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}$$
Bild: 3.2.15 och 3.2.16
Exempel 8
Bestäm medelpunkt och radie för den cirkel vars ekvation är $\ x^2 + y^2 – 2x + 4y + 1 = 0\,$.
Vi ska försöka skriva om cirkelns ekvation på formen
$$(x – a)^2 + (y – b)^2 = r^2$$
för då kan vi direkt avläsa att medelpunken är $\,(a,b)\,$ och radien är $\,r\,$.
Börja med att kvadratkomplettera termerna som innehåller $\,x\,$ i vänsterledet
$$ \underline{x^2-2x\vphantom{(}} + y^2+4y + 1 =\underline{(x-1)^2-1^2} + y^2+4y + 1$$
(de understrukna termerna visar kvadratkompletteringen).
Kvadratkomplettera sedan termerna som innehåller $y$
$$ (x-1)^2-1^2 + \underline{y^2+4y} + 1= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}$$
Vänsterledet är alltså lika med
$$ (x-1)^2 + (y+2)^2-4 $$
och flyttar vi över 4 till högerledet är cirkelns ekvation
$$ (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}$$
Vi avläser att medelpunkten är $\,(1,-2)\,$ och radien är $\,\sqrt{4}= 2\,$.
Övningar
© Copyright 2007, math.se
|
|