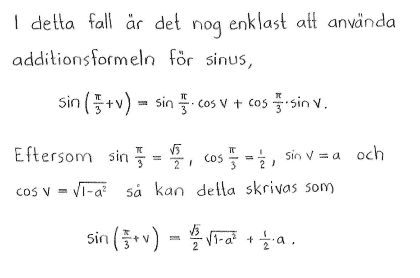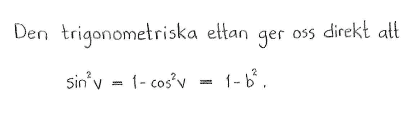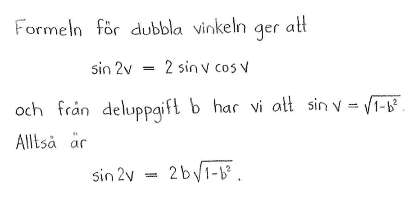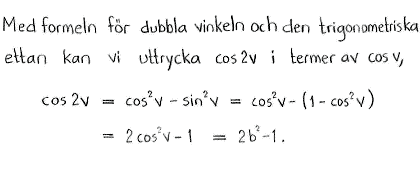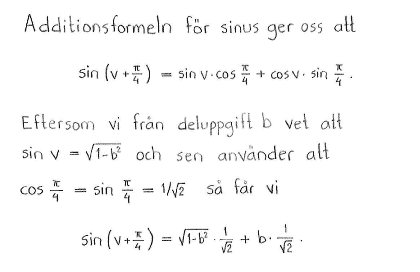4.3 Övningar
Sommarmatte 1
Innehåll |
Övning 4.3:1
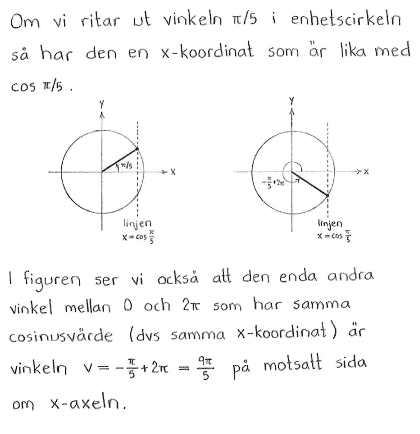
Bestäm de vinklar $v$ mellan $\displaystyle \frac{\pi}{2}$ och $2\pi$ som uppfyller
| $\textrm{a) }$ | $\cos{v}=\cos{\displaystyle \frac{\pi}{5}}$ | $\textrm{b) }$ | $\sin{v}=\sin{\displaystyle \frac{\pi}{7}}$ | $\textrm{c) }$ | $\tan{v}=\tan{\displaystyle \frac{2\pi}{7}}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $v = \displaystyle \frac{9\pi}{5}$ | $\textrm{b) }$ | $v = \displaystyle \frac{6\pi}{7}$ | $\textrm{c) }$ | $v = \displaystyle \frac{9\pi}{7}$ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Övning 4.3:2
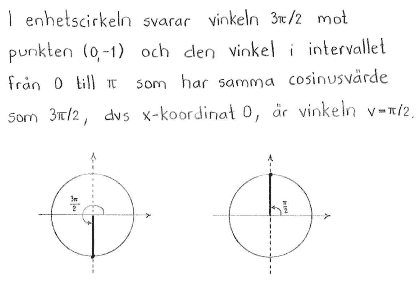
Bestäm de vinklar $v$ mellan 0 och $\pi$ som uppfyller
| $\textrm{a) }$ | $\cos{v} = \cos{\displaystyle \frac{3\pi}{2}}$ | $\textrm{b) }$ | $\cos{v} = \cos{ \displaystyle \frac{7\pi}{5}}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $v=\displaystyle \frac{\pi}{2}$ | $\textrm{b) }$ | $v=\displaystyle \frac{3\pi}{5}$ |
Lösning till delfråga a
Lösning till delfråga b
Övning 4.3:3
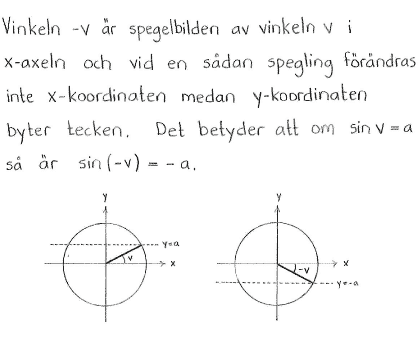
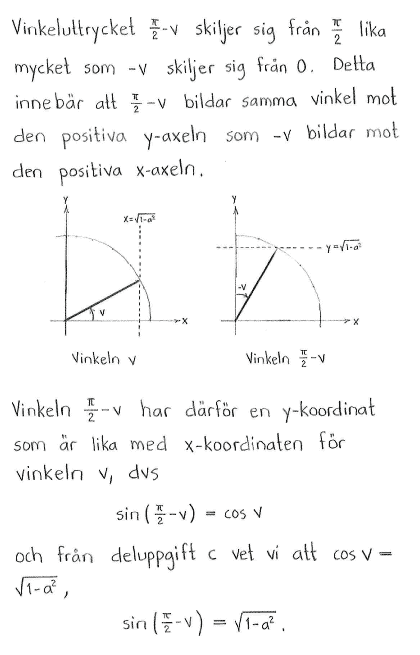
Antag att $-\displaystyle \frac{\pi}{2} \leq v \leq \displaystyle \frac{\pi}{2}$ och att $\sin{v} = a$. Uttryck med hjälp av $a$
| $\textrm{a) }$ | $\sin{(-v)}$ | $\textrm{b) }$ | $\sin{(\pi-v)}$ | $\textrm{c) }$ | $\cos{v}$ |
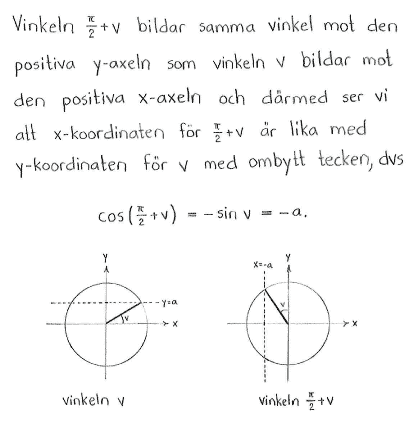
| $\textrm{d) }$ | $\sin{\left(\displaystyle \frac{\pi}{2}-v\right)}$ | $\textrm{e) }$ | $\cos{\left( \displaystyle \frac{\pi}{2} + v\right)}$ | $\textrm{f) }$ | $\sin{\left( \displaystyle \frac{\pi}{3} + v \right)}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $-a$ | $\textrm{b) }$ | $a$ | $\textrm{c) }$ | $\sqrt{1-a^2}$ |
| $\textrm{d) }$ | $\sqrt{1-a^2}$ | $\textrm{e) }$ | $-a$ | $\textrm{f) }$ | $\displaystyle \frac{\sqrt{3}}{2}\sqrt{1-a^2}+\displaystyle \frac{1}{2}\cdot a $ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
Lösning till delfråga e
Lösning till delfråga f
Övning 4.3:4
Antag att $0 \leq v \leq \pi$ och att $\cos{v}=b$. Uttryck med hjälp av $b$
| $\textrm{a) }$ | $\sin^2{v}$ | $\textrm{b) }$ | $\sin{v}$ | $\textrm{c) }$ | $\sin{2v}$ |
| $\textrm{d) }$ | $\cos{2v}$ | $\textrm{e) }$ | $\sin{\left( v+\displaystyle \frac{\pi}{4} \right)}$ | $\textrm{f) }$ | $\cos{\left( v-\displaystyle \frac{\pi}{3} \right)}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $1-b^2$ | $\textrm{b) }$ | $\sqrt{1-b^2}$ | $\textrm{c) }$ | $2b\sqrt{1-b^2}$ |
| $\textrm{d) }$ | $2b^2-1$ | $\textrm{e) }$ | $\sqrt{1-b^2}\cdot\displaystyle \frac{1}{\sqrt{2}} + b\cdot \displaystyle \frac{1}{\sqrt{2}} $ | $\textrm{f) }$ | $b\cdot\displaystyle \frac{1}{2}+\sqrt{1-b^2}\cdot\displaystyle \frac{\sqrt{3}}{2}$ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
Lösning till delfråga e
Lösning till delfråga f
