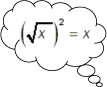3.1 Roots
From Förberedande kurs i matematik 1
| Theory | Exercises |
Contents:
- Square roots and n'th roots
- Manipulating roots
Learning outcomes:
After this section, you will have learned:
- How to calculate the square root of some simple integers.
- That the square root of a negative number is not defined.
- That the square root of a number denotes the positive root.
- How to manipulate roots in the simplification of expressions.
- To recognise when the methods of manipulating roots are valid.
- How to simplify expressions containing quadratic roots in the denominator.
- When the n'th root of a negative number is defined (n odd).
Square roots
The well-known symbol \displaystyle \sqrt{a}, the square root of \displaystyle a, is used to describe the number that when multiplied by itself gives \displaystyle a. However, one has to be a little more precise in defining this symbol.
The equation \displaystyle x^2 = 4 has two solutions \displaystyle x = 2 and \displaystyle x = -2, since both \displaystyle 2\cdot 2 = 4 and \displaystyle (-2)\cdot(-2) = 4. It would then be logical to suppose that \displaystyle \sqrt{4} can be either \displaystyle -2 or \displaystyle 2, i.e. \displaystyle \sqrt{4}= \pm 2, but \displaystyle \sqrt{4} only denotes the positive number \displaystyle 2.
The square root \displaystyle \sqrt{a} means the non-negative number that multiplied by itself gives \displaystyle a, i.e. the non-negative solution to the equation \displaystyle x^2 = a.
The square root of \displaystyle a can also be written as \displaystyle a^{1/2}.
It is therefore wrong to state that \displaystyle \sqrt{4}= \pm 2, but correct to state that the equation \displaystyle x^2 = 4 has the solution \displaystyle x = \pm 2.
Example 1
- \displaystyle \sqrt{0}=0 \quad because \displaystyle 0^2 = 0 \cdot 0 = 0 and \displaystyle 0 is not negative.
- \displaystyle \sqrt{100}=10 \quad since \displaystyle 10^2 = 10 \cdot 10 = 100 and \displaystyle 10 is a positive number.
- \displaystyle \sqrt{0_.25}=0_.5 \quad since \displaystyle 0_.5^2 = 0_.5 \cdot 0_.5 = 0_.25 and \displaystyle 0{_.}5 is positive.
- \displaystyle \sqrt{2} \approx 1{_.}4142 \quad since \displaystyle 1{_.}4142 \cdot 1{_.}4142 \approx 2 and \displaystyle 1{_.}4142 is positive.
- The equation \displaystyle x^2=2 has the solutions \displaystyle x=\sqrt{2} \approx 1{_.}414 and \displaystyle x = -\sqrt{2} \approx -1{_.}414.
- \displaystyle \sqrt{-4}\quad is not defined, since there is no real number \displaystyle x that satisfies \displaystyle x^2=-4.
- \displaystyle \sqrt{(-7)^2} = 7 \quad because \displaystyle \sqrt{(-7)^2} = \sqrt{(-7) \cdot (-7)} = \sqrt{49} = \sqrt{ 7 \cdot 7} = 7.
It is useful to know how square roots behave for calculations. As \displaystyle \sqrt{a} = a^{1/2} we can handle expressions involving roots as we would expressions involving exponents. For example, we have
\displaystyle \sqrt{9\cdot 4}
= (9\cdot 4)^{1/2}
= 9^{1/2}\cdot 4^{1/2}
= \sqrt{9}\cdot \sqrt{4}\mbox{.}
|
In this way we obtain the following rules for quadratic roots.
For all real numbers \displaystyle a, b \ge 0:
\displaystyle \begin{align*}
\sqrt{ab} &= \sqrt{\vphantom{b}a}\cdot \sqrt{b}\\[4pt]
\sqrt{\frac{a}{b}} &= \frac{\sqrt{a}}{\sqrt{b}}, \quad\ \mathrm{for}\ b\neq0\\[4pt]
a\sqrt{b} &= \sqrt{a^2b}
\end{align*}
|
Example 2
- \displaystyle \sqrt{64\cdot 81} = \sqrt{64}\cdot \sqrt{81} = 8\cdot 9 = 72
- \displaystyle \sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}
- \displaystyle \sqrt{18} \cdot \sqrt{2} = \sqrt{18 \cdot 2} = \sqrt{36} = 6
- \displaystyle \frac{\sqrt{75}}{\sqrt{3}} = \sqrt{\frac{75}{3}} = \sqrt{25} = 5
- \displaystyle \sqrt{12} = \sqrt{ 4 \cdot 3 } = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}
Note that the above calculations assume that \displaystyle a and \displaystyle b \ge 0. If \displaystyle a and \displaystyle b are negative (< 0) then \displaystyle \sqrt{a} and \displaystyle \sqrt{b} are not defined as real numbers. It is tempting to write , for example,
| \displaystyle -1 = \sqrt{-1} \cdot \sqrt{-1} = \sqrt{ (-1) \cdot (-1) } = \sqrt{1} = 1 |
but something here cannot be right. The explanation is that \displaystyle \sqrt{-1} is not a real number, which means the laws of roots discussed above may not be used.
Higher order roots
The cube root of a number \displaystyle a is defined as the number that multiplied by itself three times gives \displaystyle a, and is denoted as \displaystyle \sqrt[\scriptstyle 3]{a}.
Example 3
- \displaystyle \sqrt[\scriptstyle 3]{8} = 2 \quad as \displaystyle 2 \cdot 2 \cdot 2=8.
- \displaystyle \sqrt[\scriptstyle 3]{0{_.}027} = 0{_.}3 \quad since \displaystyle 0{_.}3 \cdot 0{_.}3 \cdot 0{_.}3 = 0{_.}027.
- \displaystyle \sqrt[\scriptstyle 3]{-8} = -2 \quad because \displaystyle (-2) \cdot (-2) \cdot (-2)= -8.
Note that, unlike square roots, cube roots are also defined for negative numbers.
For any positive integer \displaystyle n one can define the \displaystyle n'th root of a number \displaystyle a:
- if \displaystyle n is even and \displaystyle a\ge0 then \displaystyle \sqrt[\scriptstyle n]{a} is the non-negative number that when multiplied by itself \displaystyle n times gives \displaystyle a,
- if \displaystyle n is odd, \displaystyle \sqrt[\scriptstyle n]{a} is the number that when multiplied by itself \displaystyle n times gives \displaystyle a.
The root \displaystyle \sqrt[\scriptstyle n]{a} can also be written as \displaystyle a^{1/n}.
Example 4
- \displaystyle \sqrt[\scriptstyle 4]{625} = 5\quad since \displaystyle 5 \cdot 5 \cdot 5 \cdot 5 = 625.
- \displaystyle \sqrt[\scriptstyle 5]{-243} = -3\quad because \displaystyle (-3) \cdot (-3) \cdot (-3) \cdot (-3) \cdot (-3) = -243.
- \displaystyle \sqrt[\scriptstyle 6]{-17}\quad is not defined as \displaystyle 6 is even and \displaystyle -17 is a negative number.
For \displaystyle n'th roots the same rules apply as for quadratic roots if \displaystyle a, \, b \ge 0. Note that if \displaystyle n is odd these methods apply even for negative \displaystyle a and \displaystyle b, that is, for all real numbers \displaystyle a and \displaystyle b.
\displaystyle \begin{align*}
\sqrt[\scriptstyle n]{ab}
&= \sqrt[\scriptstyle n]{\vphantom{b}a}\cdot
\sqrt[\scriptstyle n]{b}\\[4pt]
\sqrt[\scriptstyle n]{\frac{a}{b}}
&= \frac{\sqrt[\scriptstyle n]{a}}{\sqrt[\scriptstyle n]{b}}, \quad\ \mathrm{for}\ b\neq0\\[4pt]
a\,\sqrt[\scriptstyle n]{b}
&= \sqrt[\scriptstyle n]{a^nb}
\end{align*}
|
Simplification of expressions containing roots
Often one can significantly simplify expressions containing roots by using the rules described above. As is also the case when dealing with exponents, it is desirable to reduce expressions into "small" roots. For example, it is a good idea to do the following
\displaystyle \sqrt{8}
= \sqrt{4\cdot2}
= \sqrt{4} \cdot \sqrt{2}
= 2\sqrt{2}
|
because it helps simplification as we see here
\displaystyle \frac{\sqrt{8}}{2}
= \frac{2 \sqrt{2}}{2}
= \sqrt{2}\mbox{.}
|
By rewriting expressions containing roots in terms of "small" roots one can also sum roots of "the same kind", e.g.
\displaystyle \sqrt{8} + \sqrt{2}
= 2\sqrt{2} + \sqrt{2}
= (2+1)\sqrt{2}
= 3\sqrt{2}\mbox{.}
|
Example 5
- \displaystyle \frac{\sqrt{8}}{\sqrt{18}} = \frac{\sqrt{2 \cdot 4}}{\sqrt{2 \cdot 9}} = \frac{\sqrt{2 \cdot 2 \cdot 2}}{\sqrt{2 \cdot 3 \cdot 3}} = \frac{\sqrt{2 \cdot 2^2}}{\sqrt{2 \cdot 3^2}} = \frac{2\sqrt{2}}{3\sqrt{2}} = \frac{2}{3}
- \displaystyle \frac{\sqrt{72}}{6} = \frac{\sqrt{8 \cdot 9}}{ 2 \cdot 3} = \frac{\sqrt{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3}}{ 2 \cdot 3} = \frac{\sqrt{2^2 \cdot 3^2 \cdot 2}}{ 2 \cdot 3} = \frac{2 \cdot 3\sqrt{2}}{2 \cdot 3} = \sqrt{2}
- \displaystyle \sqrt{45} + \sqrt{20}
= \sqrt{9\cdot5} + \sqrt{4\cdot5}
= \sqrt{3^2\cdot5} + \sqrt{2^2\cdot5}
= 3\sqrt{5} + 2\sqrt{5}\vphantom{\bigl(}
\displaystyle \phantom{\sqrt{45} + \sqrt{20}\vphantom{\bigl(}}{} = (3+2)\sqrt{5} = 5\sqrt{5} - \displaystyle \sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}
= \sqrt{5 \cdot 10} + 2\sqrt{3} -\sqrt{2 \cdot 16}
+ \sqrt{3 \cdot 9}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{5 \cdot 2 \cdot 5} + 2\sqrt{3} -\sqrt{2 \cdot 4 \cdot 4} + \sqrt{3 \cdot 3 \cdot 3}\vphantom{a^{b^c}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{5^2 \cdot 2 } + 2\sqrt{3} -\sqrt{2^2 \cdot 2^2 \cdot 2} + \sqrt{3 \cdot 3^2}\vphantom{a^{\textstyle b^{\textstyle c}}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = 5\sqrt{2} +2\sqrt{3} - 2 \cdot 2\sqrt{2} + 3\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = (5-4)\sqrt{2} + (2+3)\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{2} + 5\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}} - \displaystyle \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{12} } = \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{3 \cdot 4} } = \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{3} \cdot \sqrt[\scriptstyle3]{4} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{4} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{2 \cdot 2} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{2} \cdot \sqrt[\scriptstyle3]{2} } \cdot \displaystyle \frac{\sqrt[\scriptstyle3]{2}}{ \sqrt[\scriptstyle3]{2}} = \frac{ 2\cdot\sqrt[\scriptstyle3]{2} }{ 2 } = \sqrt[\scriptstyle3]{2}
- \displaystyle (\sqrt{3} + \sqrt{2}\,)(\sqrt{3} - \sqrt{2}\,) = (\sqrt{3}\,)^2-(\sqrt{2}\,)^2 = 3-2 = 1 where we have used the difference of two squares \displaystyle (a+b)(a-b) = a^2 - b^2 with \displaystyle a=\sqrt{3} and \displaystyle b=\sqrt{2}.
Rational root expressions
When roots appear in a rational expression it is often useful to write the expression in a form which does not contain roots in the denominator. This is because it is difficult to divide by irrational numbers in calculations by hand. In the example below, multiplying by \displaystyle 1=\frac{\sqrt{2}}{\sqrt{2}} , one obtains
\displaystyle \frac{1}{\sqrt{2}}
= \frac{1\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}
= \frac{\sqrt{2}}{2}
|
which usually is preferable.
In other cases, we can use the difference of two squares i.e \displaystyle (a+b)(a-b) = a^2 – b^2 to eliminate the root from the denominator. Indeed, if we multiply both the numerator and denominator by the denominator´s “conjugate” expression, then the root in the denominator gets squared and hence is removed. For example,
\displaystyle \begin{align*}
\frac{\sqrt{3}}{\sqrt{2}+1}
&= \frac{\sqrt{3}}{\sqrt{2}+1} \cdot \frac{\sqrt{2}-1}{\sqrt{2}-1}
= \frac{\sqrt{3}\,(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}\\[4pt]
&= \frac{\sqrt{3}\cdot\sqrt{2} - \sqrt{3}\cdot1}{(\sqrt{2}\,)^2 - 1^2 }
= \frac{\sqrt{3 \cdot 2} - \sqrt{3}}{ 2 - 1 }
= \frac{\sqrt{6} - \sqrt{3}}{ 1 }
= \sqrt{6} - \sqrt{3}\mbox{.}
\end{align*}
|
Example 6
- \displaystyle \frac{10\sqrt{3}}{\sqrt{5}} = \frac{10\sqrt{3}\cdot\sqrt{5}}{\sqrt{5}\cdot\sqrt{5}} = \frac{10\sqrt{15}}{5} = 2\sqrt{15}
- \displaystyle \frac{1+\sqrt{3}}{\sqrt{2}} = \frac{(1+\sqrt{3})\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} = \frac{\sqrt{2}+\sqrt{6}}{2}
- \displaystyle \frac{3}{\sqrt{2}-2} = \frac{3(\sqrt{2}+2)}{(\sqrt{2}-2)(\sqrt{2}+2)} = \frac{3\sqrt{2}+6}{(\sqrt{2}\,)^2-2^2} = \frac{3\sqrt{2}+6}{2-4} = -\frac{3\sqrt{2}+6}{2}
- \displaystyle \frac{\sqrt{2}}{\sqrt{6}+\sqrt{3}}
= \frac{\sqrt{2}\,(\sqrt{6}-\sqrt{3}\,)}{(\sqrt{6}+\sqrt{3}\,)
(\sqrt{6}-\sqrt{3}\,)}
= \frac{\sqrt{2}\,\sqrt{6}-\sqrt{2}\,\sqrt{3}}{(\sqrt{6}\,)^2
-(\sqrt{3}\,)^2}\vphantom{\Biggl(}
\displaystyle \phantom{\frac{\sqrt{2}}{\sqrt{6}+\sqrt{3}}\vphantom{\Biggl(}}{} = \frac{\sqrt{2}\,\sqrt{2\cdot 3}-\sqrt{2}\,\sqrt{3}}{6-3} = \frac{2\sqrt{3}-\sqrt{2}\,\sqrt{3}}{3} = \frac{(2-\sqrt{2}\,)\sqrt{3}}{3} \vphantom{\displaystyle\frac{a^{\textstyle b^{\textstyle c}}}{b}}
Study advice
Basic and final tests
After you have read the text and worked through the exercises, you should do the basic and final tests to pass this section. You can find the link to the tests in your student lounge.
Keep in mind that...
The square root of a number is always non-negative (that is, positive or zero)!
Rules for roots are actually a special case of laws of exponents, since, for example, \displaystyle \sqrt{x} = x^{1/2}.
Reviews
For those of you who want to deepen your understanding or need more detailed explanations consider the following references
Learn more about square roots from Wikipedia
How do we know that the square root of 2 is not a fraction?
Useful web sites
How to find the root of a number, without the help of calculators?