4.1 Angles and circles

From Förberedande kurs i matematik 1

Jump to: navigation, search
       Theory          Exercises      

Contents:

  • Various angle measures (degrees, radians and revolutions)
  • The Pythagorean theorem
  • Formula for distance in the plane
  • Equation of a circle

Learning outcomes:

After this section, you will have learned :

  • To convert between degrees, radians and revolutions.
  • To calculate the area and circumference of sectors of a circle.
  • The features of right-angled triangles.
  • To formulate and use the Pythagorean theorem.
  • To calculate the distance between two points in the plane.
  • To sketch circles by completing the square.
  • The concepts of the unit circle, tangent, radius, diameter, circumference, chord and arc.
  • To solve geometric problems that contain circles.

Angle measures

There are several different units for measuring angles, which are used in different contexts. The two most common within mathematics are degrees and radians.

  • Degrees. If a complete revolution is divided into 360 parts, then each part is called 1 degree. Degrees are designated by \displaystyle {}^\circ.
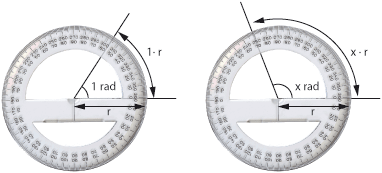
  • Radians. Another way to measure an angle, is to use the length of the arc described by the angle in relation to the radius. This unit is called radian. A revolution is \displaystyle 2\pi radians, since the circumference of a circle is \displaystyle 2\pi r, where \displaystyle r is the radius of the circle.


A complete revolution is \displaystyle 360^\circ or \displaystyle 2\pi radians which means

\displaystyle \begin{align*} 
   &1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radians }
            = \frac{\pi}{180}\ \mbox{ radians,}\\
   &1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ
            = \frac{180^\circ}{\pi}\,\mbox{.}
 \end{align*}

These conversion relations can be used to convert between degrees and radians.

Example 1

  1. \displaystyle 30^\circ = 30 \cdot 1^\circ = 30 \cdot \frac{\pi}{180}\ \mbox{ radians } = \frac{\pi}{6}\ \mbox{ radians }
  2. \displaystyle \frac{\pi}{8}\ \mbox { radians } = \frac{\pi}{8} \cdot (1 \; \mbox{radian}\,) = \frac{\pi}{8} \cdot \frac{180^\circ}{\pi} = 22\mbox{.}5^\circ

In some contexts, it may be useful to talk about negative angles and angles greater than 360°. This means that the same point on the circle can be designated by different angles that differ from each other by an integral number of revolutions.

[Image]

Example 2

  1. The angles \displaystyle -55^\circ and \displaystyle 665^\circ indicate the same point on the circle because
    \displaystyle 
     -55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}
  2. The angles \displaystyle \frac{3\pi}{7} and \displaystyle -\frac{11\pi}{7} indicate the same point on the circle because
    \displaystyle 
     \frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}
  3. The angles \displaystyle 36^\circ and \displaystyle 216^\circ do not specify the samepoint on the circle, but opposite points since
    \displaystyle 
     36^\circ + 180^\circ = 216^\circ\,\mbox{.}


Formula for distance in the plane

The theorem of Pythagoras is one of the most famous theorems in mathematics and says that in a right-angled triangle with the legs \displaystyle a and \displaystyle b, and hypotenuse \displaystyle c then \displaystyle a^2 + b^2 = c^2.

The Pythagorean theorem:
\displaystyle c^2 = a^2 + b^2\,\mbox{.}

[Image]

Example 3

Consider the triangle on the right. Then
\displaystyle c^2= 3^2 + 4^2 = 9 +16 = 25

and therefore the hypotenuse \displaystyle c is equal to

\displaystyle c=\sqrt{25} = 5\,\mbox{.}

[Image]

The Pythagorean theorem can be used to calculate the distance between two points in a coordinate system.

Formula for distance:

The distance \displaystyle d between two points with coordinates \displaystyle (x,y) and \displaystyle (a,b) is

\displaystyle d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}

The line joining the points is the hypotenuse of a triangle whose legs are parallel to the coordinate axes.

[Image]

The legs of the triangle have lengths equal to the difference in the x- and y-directions of the points, that is \displaystyle |x-a| and \displaystyle |y-b|. The Pythagorean theorem then gives the formula for the distance.

Example 4

  1. The distance between \displaystyle (1,2) and \displaystyle (3,1) is
    \displaystyle 
     d = \sqrt{ (1-3)^2 + (2-1)^2}
   = \sqrt{(-2)^2 + 1^2}
   = \sqrt{ 4+1}
   = \sqrt{5}\,\mbox{.}
  2. The distance between \displaystyle (-1,0) and \displaystyle (-2,-5) is
    \displaystyle 
     d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2}
   = \sqrt{1^2 + 5^2}
   = \sqrt{1+25}
   = \sqrt{26}\,\mbox{.}


Circles

A circle consists of all the points that are at a given fixed distance \displaystyle r from a point \displaystyle (a,b).

[Image]


The distance \displaystyle r is called the circle's radius and the point \displaystyle (a,b) is its centre. The figure below shows the other important concepts.

[Image]

[Image]

[Image]

[Image]

Diameter Tangent Chord Secant

[Image]

[Image]

[Image]

[Image]

Arc of a circle Circumference Sector of a circle Segment of a circle

Example 5

A sector of a circle is shown in the figure on the right.
  1. Determine its arc length .

    The central angle is \displaystyle 50^\circ. In radians this is
    \displaystyle 
     50^\circ = 50 \cdot 1^\circ
          = 50 \cdot \frac{\pi}{180}\ \mbox{ radians }
          = \frac{5\pi}{18}\ \mbox{ radians. }

[Image]

  1. The way radians have been defined means that the arc length is the radius multiplied by the angle measured in radians, so that the arc length is
    \displaystyle 
     3 \cdot \frac{5\pi}{18}\ \mbox{units }
 = \frac{5\pi}{6}\ \mbox{ units . }
  1. Determine the area of the circle segment.

    The segment's share of the entire circle is
    \displaystyle 
     \frac{50^\circ}{360^\circ} = \frac{5}{36}

    and this means that its area is \displaystyle \frac{5}{36} parts of the circle area, which is \displaystyle \pi r^2 = \pi 3^2 = 9\pi. Hence the area is

    \displaystyle 
     \frac{5}{36} \cdot 9\pi\ \mbox{ units }= \frac{5\pi}{4}\ \mbox{ units. }

A point \displaystyle (x,y) lies on the circle that has its centre at \displaystyle (a,b) and radius \displaystyle r, if its distance from the centre is equal to \displaystyle r. This condition can be formulated with the distance formula.

Circle equation:
\displaystyle (x – a)^2 + (y – b)^2 = r^2\,\mbox{.}

[Image]

Example 6

  1. \displaystyle (x-1)^2 + (y-2)^2 = 9\quad is the equation for a circle with centre \displaystyle (1,2) and radius \displaystyle \sqrt{9} = 3.

[Image]

  1. \displaystyle x^2 + (y-1)^2 = 1\quad can be written as \displaystyle (x-0)^2 + (y-1)^2 = 1 and is the equation of a circle with centre \displaystyle (0,1) and radius \displaystyle \sqrt{1} = 1.

[Image]

  1. \displaystyle (x+1)^2 + (y-3)^2 = 5\quad can be written as \displaystyle (x-(-1))^2 + (y-3)^2 = 5 and is the equation of a circle with centre \displaystyle (-1,3) and radius \displaystyle \sqrt{5} \approx 2\textrm{.}236.

[Image]

Example 7

  1. Does the point \displaystyle (1,2) lie on the circle \displaystyle (x-4)^2 +y^2=13?

    Inserting the coordinates of the point \displaystyle x=1 and \displaystyle y=2 in the circle equation, we have that
    \displaystyle \begin{align*} 
       \mbox{LHS } &= (1-4)^2+2^2\\
              &= (-3)^2+2^2 = 9+4 = 13 = \mbox{RHS}\,\mbox{.}
 \end{align*}

    Since the point satisfies the circle equation it lies on the circle.

    [Image]

  2. Determine the equation for the circle that has its centre at \displaystyle (3,4) and goes through the point \displaystyle (1,0).

    Since the point \displaystyle (1,0) lies on the circle, the radius of the circle must be equal to the distance of the point from \displaystyle (1,0) to the centre \displaystyle (3,4). The distance formula allows us to calculate that this distance is
    \displaystyle 
     c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{.}

    The circle equation is therefore

    \displaystyle (x-3)^2 + (y-4)^2 = 20 \; \mbox{.}

    [Image]


Example 8

Determine the centre and radius of the circle with equation \displaystyle \ x^2 + y^2 – 2x + 4y + 1 = 0.


Let us try to write the equation in the form

\displaystyle (x – a)^2 + (y – b)^2 = r^2

because then we can directly read from this that the centre is \displaystyle (a,b) and the radius is \displaystyle r.

Start by completing the square for the terms containing \displaystyle x on the left-hand side

\displaystyle 
 \underline{x^2-2x\vphantom{(}} + y^2+4y + 1
 = \underline{(x-1)^2-1^2} + y^2+4y + 1

The underlined terms shows the terms involved.

Now complete the square for the terms containing \displaystyle y

\displaystyle 
 (x-1)^2-1^2 + \underline{y^2+4y} + 1
 = (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}

The left-hand side is therefore equal to

\displaystyle (x-1)^2 + (y+2)^2-4 .

Rearranging we see that the original equation is equivalent to

\displaystyle (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}

From this we can easily see that the centre is \displaystyle (1,-2) and the radius is \displaystyle \sqrt{4}= 2.

[Image]


Exercises

Study advice

The basic and final tests

After you have read the text and worked through the exercises, you should do the basic and final tests to pass this section. You can find the link to the tests in your student lounge.


Keep in mind that...


Reviews

For those of you who want to deepen your understanding or need more detailed explanations consider the following references:

Learn more about Pythagoras theorem from Wikipedia

Read more about the circle on the Mathworld website


Useful web sites

Interactive experiments: the sine and cosine on the unit circle (Flash)

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/4.1_Angles_and_circles"