Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Solution 3.4:1b

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 3.4:1b moved to Solution 3.4:1b: Robot: moved page)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
In the equation, both sides are positive because the factors
-
<center> [[Image:3_4_1b-1(2).gif]] </center>
+
<math>e^{x}</math>
-
{{NAVCONTENT_STOP}}
+
and
-
{{NAVCONTENT_START}}
+
<math>3^{-x}</math>
-
<center> [[Image:3_4_1b-2(2).gif]] </center>
+
are positive regardless of the value of
-
{{NAVCONTENT_STOP}}
+
<math>x</math>
 +
(a positive base raised to a number always gives a positive number). We can therefore take the natural logarithm of both numbers,
 +
 
 +
 
 +
<math>\ln \left( 13e^{x} \right)=\ln \left( 2\centerdot 3^{-x} \right)</math>
 +
 
 +
 
 +
Using the log law, we can divide up the products into several logarithmic terms,
 +
 
 +
 
 +
<math>\ln 13+\ln e^{x}=\ln 2+\ln 3^{-x}</math>
 +
 
 +
 
 +
and using the law
 +
<math>\ln a^{b}=b\centerdot \ln a</math>, we can get rid of
 +
<math>x</math>
 +
from the exponents:
 +
 
 +
 
 +
<math>\ln 13+x\ln e=\ln 2+\left( -x \right)\ln 3</math>
 +
 
 +
 
 +
Collecting together
 +
<math>x</math>
 +
on one side and the other terms on the other,
 +
 
 +
 
 +
<math>x\ln e+x\ln 3=\ln 2-\ln 13</math>
 +
 
 +
 
 +
Take out
 +
<math>x</math>
 +
on the left-hand side and use
 +
<math>\ln e=1</math>
 +
:
 +
 
 +
 
 +
<math>x\left( 1+\ln 3 \right)=\ln 2-\ln 13</math>
 +
 
 +
 
 +
Then, solve for
 +
<math>x</math>
 +
:
 +
 
 +
 
 +
<math>x=\frac{\ln 2-\ln 13}{1+\ln 3}</math>
 +
 
 +
 
 +
NOTE: Because
 +
<math>\ln 2<\ln 13</math>, we can write the answer as
 +
 
 +
 
 +
<math>x=-\frac{\ln 13-\ln 2}{1+\ln 3}</math>
 +
 
 +
 
 +
in order to indicate that
 +
<math>x</math>
 +
is negative.

Revision as of 12:55, 12 September 2008

In the equation, both sides are positive because the factors ex and 3−x are positive regardless of the value of x (a positive base raised to a number always gives a positive number). We can therefore take the natural logarithm of both numbers,


ln13ex=ln23−x 


Using the log law, we can divide up the products into several logarithmic terms,


ln13+lnex=ln2+ln3−x


and using the law lnab=blna, we can get rid of x from the exponents:


ln13+xlne=ln2+−xln3 


Collecting together x on one side and the other terms on the other,


xlne+xln3=ln2−ln13


Take out x on the left-hand side and use lne=1


x1+ln3=ln2−ln13 


Then, solve for x


x=1+ln3ln2−ln13


NOTE: Because 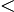ln2ln13, we can write the answer as


x=−1+ln3ln13−ln2


in order to indicate that x is negative.

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_3.4:1b"