Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Solution 2.2:6a

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 2.2:6a moved to Solution 2.2:6a: Robot: moved page)
Line 1: Line 1:
 +
According to the definition, the point of intersection between two lines is that point which lies on both lines; it must therefore satisfy the equations of both lines.
 +
 +
If the point of intersection has coordinates
 +
<math>\left( x \right.,\left. y \right)</math>, then
 +
 +
<math>y=3x+5</math>
 +
 +
and
 +
 +
<math>y=0</math>
 +
(
 +
<math>x</math>
 +
-axis)
 +
 +
If we substitute
 +
<math>y=0</math>
 +
into the first equation, we obtain
 +
 +
 +
<math>0=3x+5</math>
 +
i.e.
 +
<math>x=-\frac{5}{3}</math>
 +
 +
 +
The point of intersection is
 +
<math>\left( -\frac{5}{3} \right.,\left. 0 \right)</math>.
 +
 +
{{NAVCONTENT_START}}
{{NAVCONTENT_START}}
-
<center> [[Image:2_2_6a.gif]] </center>
+
 
[[Image:2_2_6_a.gif|center]]
[[Image:2_2_6_a.gif|center]]
{{NAVCONTENT_STOP}}
{{NAVCONTENT_STOP}}

Revision as of 10:16, 18 September 2008

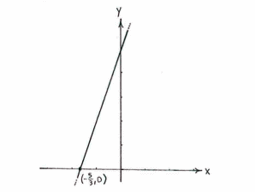
According to the definition, the point of intersection between two lines is that point which lies on both lines; it must therefore satisfy the equations of both lines.

If the point of intersection has coordinates xy , then

y=3x+5

and

y=0 ( x -axis)

If we substitute y=0 into the first equation, we obtain


0=3x+5 i.e. x=−35


The point of intersection is −350 .


Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_2.2:6a"