Solution 2.2:6e

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 2.2:6e moved to Solution 2.2:6e: Robot: moved page)
Line 1: Line 1:
 +
The lines have a point of intersection at that point which simultaneously satisfies the equations of both lines:
 +
 +
 +
<math>2x+y-1=0</math>
 +
and
 +
<math>y-2x-2=0</math>.
 +
 +
If we make
 +
<math>y</math>
 +
the subject of the second equation
 +
<math>y-2x-2=0</math>
 +
and substitute it into the first equation, we obtain an equation which only contains
 +
<math>x</math>,
 +
 +
 +
<math>2x+\left( 2x+2 \right)-1=0\ \Leftrightarrow \ 4x+1=0</math>
 +
 +
 +
which gives that
 +
<math>x=-{1}/{4}\;</math>. Then, from the relation
 +
<math>y=2x+2</math>, we obtain
 +
<math>y=2\left( -{1}/{4}\; \right)+2={3}/{2}\;</math>.
 +
 +
The point of intersection is
 +
<math>\left( -\frac{1}{4} \right.,\left. \frac{3}{2} \right)</math>.
 +
 +
We check for safety's sake that
 +
<math>\left( -\frac{1}{4} \right.,\left. \frac{3}{2} \right)</math>
 +
really satisfies both equations:
 +
 +
{{NAVCONTENT_START}}
{{NAVCONTENT_START}}
-
<center> [[Image:2_2_6e-1(2).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
-
{{NAVCONTENT_START}}
+
-
<center> [[Image:2_2_6e-2(2).gif]] </center>
+
{{NAVCONTENT_STOP}}
{{NAVCONTENT_STOP}}
[[Image:2_2_6_e.gif|center]]
[[Image:2_2_6_e.gif|center]]
 +
We check for safety's sake that
 +
<math>\left( -\frac{1}{4} \right.,\left. \frac{3}{2} \right)</math>
 +
really satisfies both equations:
 +
 +
 +
<math>2x+y-1=0</math>:
 +
LHS =
 +
<math>2\left( -\frac{1}{4} \right)+\frac{3}{2}-1=-\frac{1}{2}+\frac{3}{2}-\frac{2}{2}=0</math> =RHS
 +
 +
<math>y-2x-2=0</math>:
 +
LHS =
 +
<math>\frac{3}{2}-2\left( -\frac{1}{4} \right)-2=\frac{3}{2}+\frac{1}{2}-\frac{4}{2}=0</math> =RHS

Revision as of 12:11, 18 September 2008

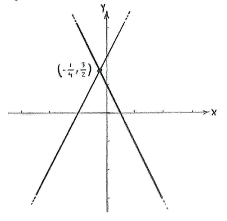
The lines have a point of intersection at that point which simultaneously satisfies the equations of both lines:


\displaystyle 2x+y-1=0 and \displaystyle y-2x-2=0.

If we make \displaystyle y the subject of the second equation \displaystyle y-2x-2=0 and substitute it into the first equation, we obtain an equation which only contains \displaystyle x,


\displaystyle 2x+\left( 2x+2 \right)-1=0\ \Leftrightarrow \ 4x+1=0


which gives that \displaystyle x=-{1}/{4}\;. Then, from the relation \displaystyle y=2x+2, we obtain \displaystyle y=2\left( -{1}/{4}\; \right)+2={3}/{2}\;.

The point of intersection is \displaystyle \left( -\frac{1}{4} \right.,\left. \frac{3}{2} \right).

We check for safety's sake that \displaystyle \left( -\frac{1}{4} \right.,\left. \frac{3}{2} \right) really satisfies both equations:


We check for safety's sake that \displaystyle \left( -\frac{1}{4} \right.,\left. \frac{3}{2} \right) really satisfies both equations:


\displaystyle 2x+y-1=0: LHS = \displaystyle 2\left( -\frac{1}{4} \right)+\frac{3}{2}-1=-\frac{1}{2}+\frac{3}{2}-\frac{2}{2}=0 =RHS

\displaystyle y-2x-2=0: LHS = \displaystyle \frac{3}{2}-2\left( -\frac{1}{4} \right)-2=\frac{3}{2}+\frac{1}{2}-\frac{4}{2}=0 =RHS

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_2.2:6e"