Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Solution 2.2:8b

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 2.2:8b moved to Solution 2.2:8b: Robot: moved page)
Line 1: Line 1:
 +
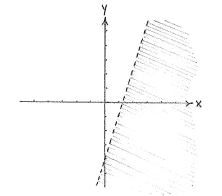
A point whose coordinates satisfy
 +
<math>y<3x-4</math>
 +
has a
 +
<math>y</math>
 +
-coordinate which is less than that of a point lying on the line
 +
<math>y=3x-4</math>
 +
and having the same
 +
<math>x</math>
 +
-coordinate. This means that the area we should shade consists of all points below the line
 +
<math>y=3x-4</math>.
 +
{{NAVCONTENT_START}}
{{NAVCONTENT_START}}
-
<center> [[Image:2_2_8b.gif]] </center>
+
 
{{NAVCONTENT_STOP}}
{{NAVCONTENT_STOP}}
[[Image:2_2_8_b.gif|center]]
[[Image:2_2_8_b.gif|center]]
 +
 +
We can draw the line
 +
<math>y=3x-4</math>
 +
by choosing two x-values, for example
 +
<math>x=0</math>
 +
and
 +
<math>x=1</math>, using the equation of the line to calculate the corresponding y-coordinates,
 +
<math>y=3\centerdot 0-4=-4</math>
 +
and
 +
<math>y=3\centerdot 1-4=-1</math>
 +
respectively, and then draw a straight line between the two points that we have obtained.

Revision as of 12:34, 18 September 2008

A point whose coordinates satisfy y3x−4 has a y -coordinate which is less than that of a point lying on the line y=3x−4 and having the same x -coordinate. This means that the area we should shade consists of all points below the line y=3x−4.

We can draw the line y=3x−4 by choosing two x-values, for example x=0 and x=1, using the equation of the line to calculate the corresponding y-coordinates, y=30−4=−4 and y=31−4=−1 respectively, and then draw a straight line between the two points that we have obtained.

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_2.2:8b"