Processing Math: Done
Solution 2.1:6a
From Förberedande kurs i matematik 1
(Difference between revisions)
m |
|||
| Line 1: | Line 1: | ||
| - | Before we try dealing with the whole expression, we focus on simplifying the two factors individually by rewriting them using a common denominator | + | Before we try dealing with the whole expression, we focus on simplifying the two factors individually by rewriting them using a common denominator |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>\begin{align} | ||
| + | x-y+\frac{x^{2}}{y-x} &= \frac{\left( x-y \right)\left( y-x \right)}{y-x}+\frac{x^{2}}{y-x} = \{\ y-x=-(x-y)\ \}\\[5pt] | ||
| + | &= \frac{-(x-y)^{2}}{y-x}+\frac{x^{2}}{y-x} = \frac{-(x-y)^{2}+x^{2}}{y-x}\\[5pt] | ||
| + | &= \frac{-(x^{2}-2xy+y^{2})+x^{2}}{y-x} = \frac{-x^{2}+2xy-y^{2}+x^{2}}{y-x}\\[5pt] | ||
| + | &= \frac{2xy-y^{2}}{y-x} = \frac{y(2x-y)}{y-x},\\[15pt] | ||
| + | \frac{y}{2x-y}-1 | ||
| + | &= \frac{y}{2x-y}-\frac{2x-y}{2x-y} = \frac{y-(2x-y)}{2x-y} = \frac{y-2x+y}{2x-y}\\[5pt] | ||
| + | & =\frac{2y-2x}{2x-y} = \frac{2(y-x)}{2x-y}\,\textrm{.} | ||
| + | \end{align}</math>}} | ||
Then, we multiply the factors together and simplify by elimination: | Then, we multiply the factors together and simplify by elimination: | ||
| - | + | {{Displayed math||<math>\biggl(x-y+\frac{x^{2}}{y-x}\biggr) \biggl(\frac{y}{2x-y}-1\biggr) = \frac{y(2x-y)}{y-x}\cdot\frac{2(y-x)}{2x-y}=2y\,\textrm{.}</math>}} | |
| - | <math>\ | + | |
Current revision
Before we try dealing with the whole expression, we focus on simplifying the two factors individually by rewriting them using a common denominator
 x−y x−y  y−x y−x +x2y−x= +x2y−x=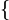 y−x=−(x−y) y−x=−(x−y) 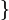 =y−x−(x−y)2+x2y−x=y−x−(x−y)2+x2=y−x−(x2−2xy+y2)+x2=y−x−x2+2xy−y2+x2=y−x2xy−y2=y−xy(2x−y) =y−x−(x−y)2+x2y−x=y−x−(x−y)2+x2=y−x−(x2−2xy+y2)+x2=y−x−x2+2xy−y2+x2=y−x2xy−y2=y−xy(2x−y) =y2x−y−2x−y2x−y=2x−yy−(2x−y)=2x−yy−2x+y=2x−y2y−2x=2x−y2(y−x). =y2x−y−2x−y2x−y=2x−yy−(2x−y)=2x−yy−2x+y=2x−y2y−2x=2x−y2(y−x). |
Then, we multiply the factors together and simplify by elimination:
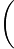 x−y+x2y−x x−y+x2y−x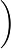 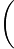 y2x−y−1 y2x−y−1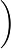 =y−xy(2x−y) =y−xy(2x−y) 2x−y2(y−x)=2y. 2x−y2(y−x)=2y. |
