Solution 2.2:5e

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 2.2:5e moved to Solution 2.2:5e: Robot: moved page)
Current revision (12:54, 24 September 2008) (edit) (undo)
m
 
(One intermediate revision not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
The line should go through the points (5,0) and (0,-8) which must therefore satisfy the equation of the line <math>y=kx+m</math>, i.e.
-
[[Image:S1_2_2_5_e.jpg|400px]]
+
 
-
<!--<center> [[Image:2_2_5e.gif]] </center>-->
+
{{Displayed math||<math>0=k\cdot 5+m\qquad\text{and}\qquad -8 = k\cdot 0+m\,\textrm{.}</math>}}
-
{{NAVCONTENT_STOP}}
+
 
 +
From the second equation, we get <math>m=-8</math> and substituting this into the first equation gives
 +
 
 +
{{Displayed math||<math>0=5k-8\quad\Leftrightarrow\quad k={8}/{5}\,\textrm{.}</math>}}
 +
 
 +
The slope of the line is 8/5.
 +
 
 +
 
 +
<center>[[Image:S1_2_2_5_e.jpg|400px]]</center>

Current revision

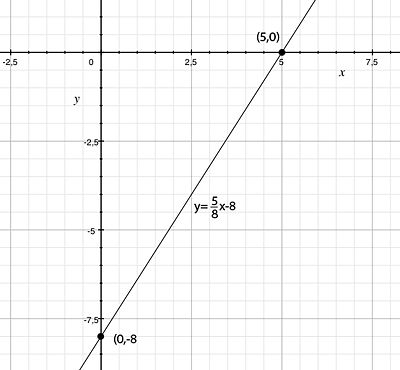
The line should go through the points (5,0) and (0,-8) which must therefore satisfy the equation of the line \displaystyle y=kx+m, i.e.

\displaystyle 0=k\cdot 5+m\qquad\text{and}\qquad -8 = k\cdot 0+m\,\textrm{.}

From the second equation, we get \displaystyle m=-8 and substituting this into the first equation gives

\displaystyle 0=5k-8\quad\Leftrightarrow\quad k={8}/{5}\,\textrm{.}

The slope of the line is 8/5.


Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_2.2:5e"