Solution 3.4:3c
From Förberedande kurs i matematik 1
m (Lösning 3.4:3c moved to Solution 3.4:3c: Robot: moved page) |
|||
| Line 1: | Line 1: | ||
| - | {{ | + | With the log laws, we can write the left-hand side as one logarithmic expression, |
| - | < | + | |
| - | {{ | + | |
| - | {{ | + | <math>\ln x+\ln \left( x+4 \right)=\ln \left( x\left( x+4 \right) \right)</math> |
| - | < | + | |
| - | {{ | + | |
| + | but this rewriting presupposes that the expressions | ||
| + | <math>\text{ln }x\text{ }</math> | ||
| + | and | ||
| + | <math>\text{ln}\left( x+\text{4} \right)</math> | ||
| + | are defined, i.e. | ||
| + | <math>x>0</math> | ||
| + | and | ||
| + | <math>x+\text{4}>0</math>. Therefore, if we choose to continue with the equation | ||
| + | |||
| + | |||
| + | <math>\ln \left( x\left( x+4 \right) \right)=\ln \left( 2x+3 \right)</math> | ||
| + | |||
| + | |||
| + | we must remember to permit only solutions that satisfy | ||
| + | <math>x>0</math> | ||
| + | (the condition | ||
| + | <math>x+\text{4}>0</math> | ||
| + | is then automatically satisfied). | ||
| + | |||
| + | The equation rewritten in this way is, in turn, only satisfied if the arguments | ||
| + | <math>x\left( x+\text{4} \right)\text{ }</math> | ||
| + | and | ||
| + | <math>\text{2}x+\text{3}</math> | ||
| + | are equal to each other and positive, i.e. | ||
| + | |||
| + | |||
| + | <math>x\left( x+\text{4} \right)=\text{2}x+\text{3}</math> | ||
| + | |||
| + | |||
| + | We rewrite this equation as | ||
| + | <math>x^{\text{2}}-\text{2}x-\text{3}=0</math> | ||
| + | and completing the square gives | ||
| + | |||
| + | |||
| + | <math>\begin{align} | ||
| + | & \left( x+1 \right)^{2}-1^{2}-3=0 \\ | ||
| + | & \left( x+1 \right)^{2}=4 \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | |||
| + | which means that | ||
| + | <math>x=-\text{1}\pm \text{2}</math>, i.e. | ||
| + | <math>x=-\text{3}</math> | ||
| + | and | ||
| + | <math>x=\text{1}</math>. | ||
| + | |||
| + | Because | ||
| + | <math>x=-\text{3}</math> | ||
| + | is negative, we neglect it, whilst for | ||
| + | <math>x=\text{1}</math> | ||
| + | we have both that | ||
| + | <math>x>0\text{ }</math> | ||
| + | and | ||
| + | <math>x\left( x+\text{4} \right)=\text{2}x+\text{3}>0</math>. Therefore, the answer is | ||
| + | <math>x=\text{1}</math>. | ||
Revision as of 12:05, 26 September 2008
With the log laws, we can write the left-hand side as one logarithmic expression,
 x+4
x+4 =ln
=ln x
x x+4
x+4

but this rewriting presupposes that the expressions
 x+4
x+4
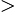 0
0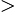 0
0
 x
x x+4
x+4
 =ln
=ln 2x+3
2x+3
we must remember to permit only solutions that satisfy
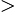 0
0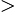 0
0
The equation rewritten in this way is, in turn, only satisfied if the arguments
 x+4
x+4
 x+4
x+4 =2x+3
=2x+3
We rewrite this equation as
 x+1
x+1 2−12−3=0
2−12−3=0 x+1
x+1 2=4
2=4
which means that
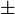 2
2
Because
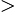 0
0  x+4
x+4 =2x+3
=2x+3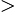 0
0
