Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Solution 2.3:6a

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (11:29, 29 September 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
Using the squaring rule, we recognize the polynomial as the expansion of
+
Using the rule <math>(a+b)^2=a^2+2ab+b^2</math>, we recognize the polynomial as the expansion of <math>(x-1)^{2}\,</math>,
-
<math>\left( x-1 \right)^{2}</math>,
+
 +
{{Displayed math||<math>x^{2}-2x+1 = (x-1)^{2}\,\textrm{.}</math>}}
-
<math>x^{2}-2x+1=\left( x-1 \right)^{2}</math>
+
This quadratic expression has its smallest value, zero, when <math>x-1=0</math>, i.e.
 +
<math>x=1</math>. All non-zero values of <math>x-1</math> give a positive value for
 +
<math>(x-1)^{2}</math>.
-
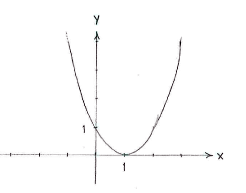
This quadratic expression has its smallest value, zero, when
+
Note: If we draw the curve <math>y=(x-1)^{2}</math>, we see that it has a minimum value of zero at <math>x=1\,</math>.
-
<math>x-\text{1}=0</math>, i.e.
+
-
<math>x=\text{1}</math>. All non-zero values of
+
-
<math>x-\text{1}</math>
+
-
give a positive value for
+
-
<math>\left( x-1 \right)^{2}</math>.
+
-
 
+
-
NOTE: If we draw the curve
+
-
<math>y=\left( x-1 \right)^{2}</math>, we see that it has a minimum value of zero at
+
-
<math>x=\text{1}</math>.
+
[[Image:2_3_6_a.gif|center]]
[[Image:2_3_6_a.gif|center]]

Current revision

Using the rule (a+b)2=a2+2ab+b2, we recognize the polynomial as the expansion of (x−1)2,

x2−2x+1=(x−1)2.

This quadratic expression has its smallest value, zero, when x−1=0, i.e. x=1. All non-zero values of x−1 give a positive value for (x−1)2.


Note: If we draw the curve y=(x−1)2, we see that it has a minimum value of zero at x=1.


Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_2.3:6a"