Processing Math: Done
Solution 3.3:3h
From Förberedande kurs i matematik 1
(Difference between revisions)
m (Lösning 3.3:3h moved to Solution 3.3:3h: Robot: moved page) |
m |
||
| (One intermediate revision not shown.) | |||
| Line 1: | Line 1: | ||
| - | {{ | + | Because <math>a^{2}\sqrt{a} = a^{2}a^{1/2} = a^{2+1/2} = a^{5/2}</math>, the logarithm law, <math>b\lg a = \lg a^b</math>, gives that |
| - | < | + | |
| - | {{ | + | {{Displayed math||<math>\log_{a} \bigl(a^{2}\sqrt{a}\,\bigr) = \log_{a}a^{5/2} = \frac{5}{2}\cdot\log_{a}a = \frac{5}{2}\cdot 1 = \frac{5}{2}\,,</math>}} |
| + | |||
| + | where we have used that <math>\log_{a}a = 1\,</math>. | ||
| + | |||
| + | |||
| + | Note: In this exercise, we assume, implicitly, that <math>a > 0</math> and <math>a\ne 1\,</math>. | ||
Current revision
Because  a=a2a1
a=a2a1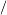 2=a2+1
2=a2+1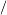 2=a5
2=a5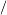 2
2
 a2 a2 a a =logaa5 =logaa5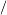 2=25 2=25 logaa=25 logaa=25 1=25 1=25 |
where we have used that
Note: In this exercise, we assume, implicitly, that 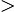 0
0 =1
=1
