Processing Math: Done
Solution 3.4:1a
From Förberedande kurs i matematik 1
(Difference between revisions)
(Ny sida: {{NAVCONTENT_START}} <center> Bild:3_4_1a-1(2).gif </center> {{NAVCONTENT_STOP}} {{NAVCONTENT_START}} <center> Bild:3_4_1a-2(2).gif </center> {{NAVCONTENT_STOP}}) |
m |
||
| (3 intermediate revisions not shown.) | |||
| Line 1: | Line 1: | ||
| - | {{ | + | We solve an equation of this type by taking the natural logarithm of both sides |
| - | < | + | |
| - | {{ | + | {{Displayed math||<math>\ln e^x = \ln 13\,\textrm{.}</math>}} |
| - | {{ | + | |
| - | < | + | Then, using the log law <math>\ln a^{b} = b\cdot \ln a</math>, the unknown <math>x</math> can then be moved down as a factor on the left-hand side |
| - | { | + | |
| + | {{Displayed math||<math>x\cdot \ln e = \ln 13</math>}} | ||
| + | |||
| + | and then it is simple to solve for <math>x</math>, | ||
| + | |||
| + | {{Displayed math||<math>x = \frac{\ln 13}{\ln e} = \frac{\ln 13}{1} = \ln 13\,\textrm{.}</math>}} | ||
| + | |||
| + | |||
| + | Note: One thing that we haven't mentioned in this solution is that before we carry out the first step and take the logarithm of both sides of the equation, it is necessary to be certain that the left- and right-hand sides are positive (it is not possible to take the logarithm of a negative number). Because the equation is | ||
| + | |||
| + | {{Displayed math||<math>e^x=13</math>}} | ||
| + | |||
| + | we see directly that the right-hand side is positive. The left-hand side is also positive because “a positive number <math>e\approx 2\textrm{.}718</math> raised to a number” always gives a positive number. | ||
Current revision
We solve an equation of this type by taking the natural logarithm of both sides
Then, using the log law  lna
lna
 lne=ln13 lne=ln13 |
and then it is simple to solve for
Note: One thing that we haven't mentioned in this solution is that before we carry out the first step and take the logarithm of both sides of the equation, it is necessary to be certain that the left- and right-hand sides are positive (it is not possible to take the logarithm of a negative number). Because the equation is
we see directly that the right-hand side is positive. The left-hand side is also positive because “a positive number 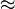 2.718
2.718
