Processing Math: Done

From Förberedande kurs i matematik 1

Revision as of 07:05, 21 August 2008 (edit) Tekbot (Talk | contribs) m (Robot: Automated text replacement (-[[Bild: +[[Image:)) ← Previous diff		Current revision (10:47, 7 October 2008) (edit) (undo) Tek (Talk | contribs) m
(2 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	A circle is defined as all the points which have a fixed distance to the circle's midpoint. Hence, a point (''x'',''y'') lies on our circle if and only if its distance to the point (1,3) is exactly 2. Using the distance formula, we can express this condition as
-	[[Image:4_1_5_a.gif|center]]	+
-	<center> [[Image:4_1_5a.gif]] </center>	+	{{Displayed math||<math>\sqrt{(x-1)^2 + (y-2)^2} = 2\,\textrm{.}</math>}}
-	{{NAVCONTENT_STOP}}	+
		+	After squaring, we obtain the equation of the circle in standard form,
		+
		+	{{Displayed math||<math>(x-1)^2 + (y-2)^2 = 4\,\textrm{.}</math>}}
		+
		+
		+	[[Image:4_1_5_a.gif|center]]

---

Current revision

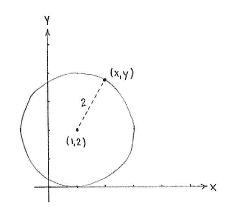
A circle is defined as all the points which have a fixed distance to the circle's midpoint. Hence, a point (x,y) lies on our circle if and only if its distance to the point (1,3) is exactly 2. Using the distance formula, we can express this condition as

(x−1)2+(y−2)2=2.

After squaring, we obtain the equation of the circle in standard form,

(x−1)2+(y−2)2=4.