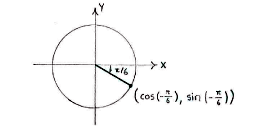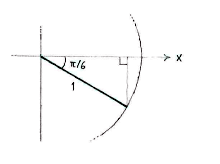Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Solution 4.2:3f

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
(Ny sida: {{NAVCONTENT_START}} <center> Bild:4_2_3f-1(2).gif </center> {{NAVCONTENT_STOP}} {{NAVCONTENT_START}} <center> Bild:4_2_3f-2(2).gif </center> {{NAVCONTENT_STOP}})
Current revision (08:21, 9 October 2008) (edit) (undo)
m
 
(5 intermediate revisions not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
The point on the unit circle which corresponds to the angle <math>-\pi/6</math> lies in the fourth quadrant.
-
<center> [[Bild:4_2_3f-1(2).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
[[Image:4_2_3_f1.gif||center]]
-
{{NAVCONTENT_START}}
+
 
-
<center> [[Bild:4_2_3f-2(2).gif]] </center>
+
As usual, <math>\cos (-\pi/6)</math> gives the ''x''-coordinate of the point of intersection between the angle's line and the unit circle. In order to determine this point, we introduce an auxiliary triangle in the fourth quadrant.
-
{{NAVCONTENT_STOP}}
+
 
 +
[[Image:4_2_3_f2.gif||center]]
 +
 
 +
We can determine the edges in this triangle by simple trigonometry and then translate these over to the point's coordinates.
 +
 
 +
{| width="100%"
 +
|width="50%" align="center"|[[Image:4_2_3_f3.gif]]
 +
|width="50%" align="left"|<math>\begin{align}\text{opposite} &= 1\cdot\sin\frac{\pi}{6} = \frac{1}{2}\\[5pt] \text{adjacent} &= 1\cdot\cos\frac{\pi}{6} = \frac{\sqrt{3}}{2}\end{align}</math>
 +
|}
 +
 
 +
The coordinates of the point of intersection are <math>(\sqrt{3}/2,-1/2)</math> and in particular <math>\cos (-\pi/6) = \sqrt{3}/2\,</math>.

Current revision

The point on the unit circle which corresponds to the angle −6 lies in the fourth quadrant.

As usual, cos(−6) gives the x-coordinate of the point of intersection between the angle's line and the unit circle. In order to determine this point, we introduce an auxiliary triangle in the fourth quadrant.

We can determine the edges in this triangle by simple trigonometry and then translate these over to the point's coordinates.

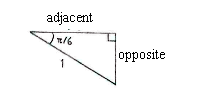
Image:4_2_3_f3.gif oppositeadjacent=1sin6=21=1cos6=23

The coordinates of the point of intersection are (32−12)  and in particular cos(−6)=32 .

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.2:3f"