From Förberedande kurs i matematik 1

Revision as of 09:45, 9 September 2008 (edit) Tekbot (Talk | contribs) m (Lösning 4.2:4a moved to Solution 4.2:4a: Robot: moved page) ← Previous diff		Current revision (08:27, 9 October 2008) (edit) (undo) Tek (Talk | contribs) m
(One intermediate revision not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	It can be a little difficult to draw the angle <math>11\pi/6</math> straight onto a unit circle, but if we rewrite <math>11\pi/6</math> as
-	<center> [[Image:4_2_4a.gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	{{Displayed math||<math>\frac{11\pi}{6} = \frac{6\pi+3\pi+2\pi}{6} = \pi + \frac{\pi}{2} + \frac{\pi}{3}</math>}}
		+
		+	we see that we have an angle that lies in the fourth quadrant, as in the figure below to the left.
		+
		+	We also note that this angle corresponds to exactly the same point on the unit circle as the angle <math>-\pi/6</math>, and because we calculated <math>\cos (-\pi/6)</math> in exercise 4.2:3f, we have that
		+
		+	{{Displayed math||<math>\cos\frac{11\pi}{6} = \cos\Bigl(-\frac{\pi}{6}\Bigr) = \frac{\sqrt{3}}{2}\,\textrm{.}</math>}}
		+
	[[Image:4_2_4_a.gif|center]]		[[Image:4_2_4_a.gif|center]]

---

Current revision

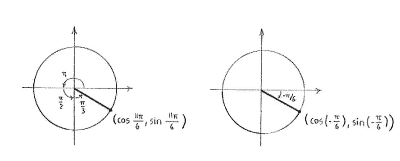
It can be a little difficult to draw the angle \displaystyle 11\pi/6 straight onto a unit circle, but if we rewrite \displaystyle 11\pi/6 as

\displaystyle \frac{11\pi}{6} = \frac{6\pi+3\pi+2\pi}{6} = \pi + \frac{\pi}{2} + \frac{\pi}{3}

we see that we have an angle that lies in the fourth quadrant, as in the figure below to the left.

We also note that this angle corresponds to exactly the same point on the unit circle as the angle \displaystyle -\pi/6, and because we calculated \displaystyle \cos (-\pi/6) in exercise 4.2:3f, we have that

\displaystyle \cos\frac{11\pi}{6} = \cos\Bigl(-\frac{\pi}{6}\Bigr) = \frac{\sqrt{3}}{2}\,\textrm{.}