Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Solution 4.4:1g

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 4.4:1g moved to Solution 4.4:1g: Robot: moved page)
Current revision (13:54, 10 October 2008) (edit) (undo)
m
 
(One intermediate revision not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
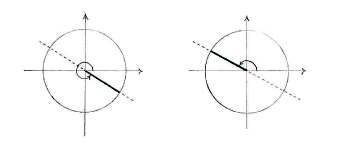
A quick sketch of the unit circle and the line <math>y=(-1/\!\sqrt{3})x</math>, which corresponds to the tangent value <math>-1/\!\sqrt{3}</math> shows that there are two angles which satisfy <math>\tan v = -1/\!\sqrt{3}</math>. One of the angles lies in the fourth quadrant and the other is the opposite angle in the second quadrant.
-
<center> [[Image:4_4_1g-1(2).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
-
{{NAVCONTENT_START}}
+
-
<center> [[Image:4_4_1g-2(2).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
-
 
+
[[Image:4_4_1_g1.gif|center]]
[[Image:4_4_1_g1.gif|center]]
 +
 +
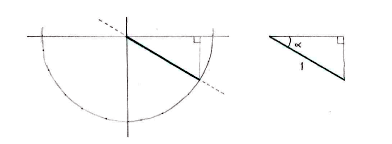
We can therefore limit ourselves to the fourth quadrant and draw an auxiliary triangle in order to determine the angle there.
[[Image:4_4_1_g2.gif|center]]
[[Image:4_4_1_g2.gif|center]]
 +
 +
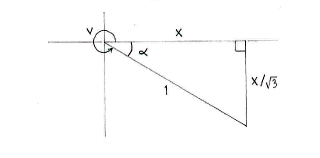
If we call <math>x</math> the side adjacent to the angle <math>\alpha</math> then the fact that <math>\tan v=-1/\!\sqrt{3}</math> gives the length of the opposite side as <math>x/\!\sqrt{3}</math>.
[[Image:4_4_1_g3.gif|center]]
[[Image:4_4_1_g3.gif|center]]
 +
 +
The Pythagorean theorem gives
 +
 +
{{Displayed math||<math>x^2 + \Bigl(\frac{x}{\sqrt{3}}\Bigr)^2 = 1^2</math>}}
 +
 +
and this equation has the solution <math>x = \sqrt{3}/2</math>, which means that
 +
 +
{{Displayed math||<math>\cos\alpha = \frac{\sqrt{3}/2}{1} = \frac{\sqrt{3}}{2}\,,</math>}}
 +
 +
i.e. <math>\alpha = \pi/6</math>. Because the angle <math>v</math> in the fourth quadrant is the complement of <math>\alpha</math> the angle <math>v</math> is given by
 +
 +
{{Displayed math||<math>v = 2\pi - \alpha = 2\pi - \frac{\pi}{6} = \frac{11\pi }{6}\,\textrm{.}</math>}}
 +
 +
If we subtract half a turn, <math>\pi</math>, we obtain the other angle
 +
 +
{{Displayed math||<math>v = \frac{11\pi}{6} - \pi = \frac{5\pi}{6}\,\textrm{.}</math>}}

Current revision

A quick sketch of the unit circle and the line y=(−13)x , which corresponds to the tangent value −13  shows that there are two angles which satisfy tanv=−13 . One of the angles lies in the fourth quadrant and the other is the opposite angle in the second quadrant.

We can therefore limit ourselves to the fourth quadrant and draw an auxiliary triangle in order to determine the angle there.

If we call x the side adjacent to the angle then the fact that tanv=−13  gives the length of the opposite side as x3 .

The Pythagorean theorem gives

x2+x32=12 

and this equation has the solution x=32 , which means that

cos=132=23 

i.e. =6. Because the angle v in the fourth quadrant is the complement of the angle v is given by

v=2−=2−6=611.

If we subtract half a turn, , we obtain the other angle

v=611−=65.
Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.4:1g"