Processing Math: Done
Solution 4.4:3c
From Förberedande kurs i matematik 1
(Difference between revisions)
(Ny sida: {{NAVCONTENT_START}} <center> Bild:4_4_3c.gif </center> {{NAVCONTENT_STOP}}) |
m |
||
| (4 intermediate revisions not shown.) | |||
| Line 1: | Line 1: | ||
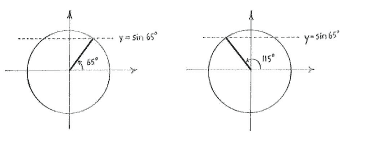
| - | {{ | + | If we consider the entire expression <math>x + 40^{\circ}</math> as an unknown, we have a basic trigonometric equation and can, with the aid of the unit circle, see that there are two solutions to the equation for <math>0^{\circ}\le x+40^{\circ}\le 360^{\circ}</math> namely <math>x+40^{\circ} = 65^{\circ}</math> and the symmetric solution <math>x + 40^{\circ} = 180^{\circ} - 65^{\circ} = 115^{\circ}\,</math>. |
| - | < | + | |
| - | {{ | + | [[Image:4_4_3_c.gif|center]] |
| + | |||
| + | It is then easy to set up the general solution by adding multiples of <math>360^{\circ}\,</math>, | ||
| + | |||
| + | {{Displayed math||<math>x + 40^{\circ} = 65^{\circ} + n\cdot 360^{\circ}\qquad\text{and}\qquad x + 40^{\circ} = 115^{\circ} + n\cdot 360^{\circ}</math>}} | ||
| + | |||
| + | for all integers ''n'', which gives | ||
| + | |||
| + | {{Displayed math||<math>x = 25^{\circ} + n\cdot 360^{\circ}\qquad\text{and}\qquad x=75^{\circ} + n\cdot 360^{\circ}\,\textrm{.}</math>}} | ||
Current revision
If we consider the entire expression 
x+40360=65=180−65=115
It is then easy to set up the general solution by adding multiples of
=65+n 360andx+40=115+n360 |
for all integers n, which gives
| +n360andx=75+n360. |
